POJ 1390 Blocks(记忆化搜索+dp)

POJ 1390 Blocks

砌块

时限：5000 MS		内存限制：65536K
提交材料共计： 6204		接受： 2563

描述

你们中的一些人可能玩过一个叫做“积木”的游戏。一行有n个块，每个盒子都有一个颜色。这是一个例子：金，银，铜，金。
相应的图片如下：
 
图1
如果一些相邻的盒子都是相同的颜色，并且它左边的盒子(如果它存在)和它的右边的盒子(如果它存在)都是其他颜色的，我们称它为“盒子段”。有四个盒子段。那就是：金，银，铜，金。片段中分别有1，4，3，1方框。

每次您可以单击一个框，然后包含该框的整个段消失。如果这段是由k个方框组成的，你会得到k*k点。例如，如果你点击一个银盒子，银段消失了，你得到4*4=16点。

现在让我们看看下面的图片：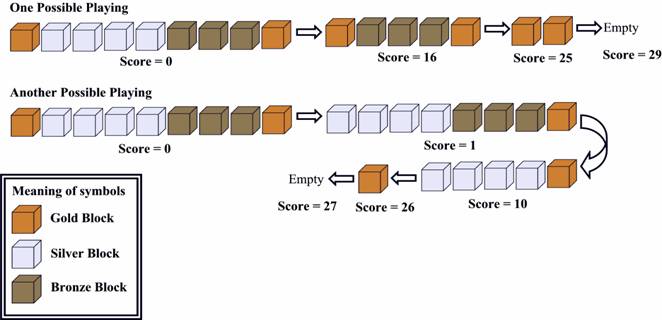
 
图2

第一个是最优的。

在这个游戏的初始状态下，找出你能得到的最高分数。

输入

第一行包含测试数t(1<=t<=15)。每个案例包含两行。第一行包含整数n(1<=n<=200)，即框数。第二行包含n个整数，表示每个框的颜色。整数在1~n的范围内。

输出量

对于每个测试用例，打印用例编号和最高可能的分数。

样本输入

2
9
1 2 2 2 2 3 3 3 1
1
1

样本输出

Case 1: 29
Case 2: 1

解题思路：

将连续的若干个方块作为一个“大块”(box_segment) 考虑，假设开始一共有 n个“大块”，编号0到n-1 第i个大块的颜色是 color[i],包含的方块数目，即长度,是len[i]

用click_box(i,j)表示从大块i到大块j这一段消除后所能 得到的最高分，则整个问题就是： click_box(0,n-1)。

要求click_box(i,j)时，考虑最右边的大块j，对它有两种处理方式，要取其优者：

1) 直接消除它，此时能得到最高分就是： click_box(i,j-1) + len[j]*len[j]

2) 期待以后它能和左边的某个同色大块合并，考虑和左边的某个同色大块合并:

左边的同色大块可能有很多个，到底和哪个合并最 好，不知道，只能枚举。假设大块j和左边的大块 k(i<=k<j-1) 合并，此时能得到的最高分是多少呢？

是不是： click_box(i,k-1) + click_box(k+1,j-1) + (len[k]+len[j])

不对！ 因为将大块k和大块j合并后，形成的新大块会在最右边。但直接将其消去，未必是最好的，也许它还应该和左边的同色大块合并，才更好

那么上面的dp不可用，需要改变问题的形式

__________________________________________________________________

click_box(i,j,ex_len) 表示: 大块 j 的右边已经有一个长度为ex_len的大块(该大块可能是在合并过程中形成的)，且 j 的颜色和ex_len相同，在此情况下所能得到的最高分 。

于是整个问题就是求：click_box(0,n-1,0)

求click_box(i,j,ex_len)时，有两种处理方法取最优者，假设j和ex_len合并后的大块称作 Q

1) 将Q直接消除，这种做法能得到的最高分就是：  click_box(i,j-1,0) + (len[j]+ex_len)2

2) 期待Q以后能和左边的某个同色大块合并。需要枚举可能和Q 合并的大块。假设让大块k和Q合并，则此时能得到的最大分数是：

　　click_box(i,k,len[j]+ex_len) + click_box(k+1,j-1,0)

click_box(i,j,ex_len) 递归的终止条件： i == j

代码：

#include<iostream>
#include<cstring>
using namespace std;
#define N 200 + 5
int dp[N][N][N];
struct segMent {
    int len;
    int color;
};
segMent segNum[N];
int clickBox(int i, int j, int len) {
    if(dp[i][j][len] != -) return dp[i][j][len];
    int result = (segNum[j].len + len)*(segNum[j].len + len);
    if(i == j) return result;
    result += clickBox(i, j-, );
    for(int k = i; k < j; k++) {
        if(segNum[k].color != segNum[j].color) continue;
        int r = clickBox(k+, j-, ) + clickBox(i, k, segNum[j].len + len);
        result = max(result, r);
    }
    dp[i][j][len] = result;
    return result;
}
int main() {
    int T;
    cin >> T;
    for(int t = ; t <= T; t++) {
        int n;
        cin >> n;
        int last = -;
        int count = -;
        memset(dp, -, sizeof(dp));
        for(int i = ; i < n; i++) {
            int v;
            cin >> v;
            if(v != last) {
                count++;
                segNum[count].len = ;
                segNum[count].color = v;
                last = v;
            } else segNum[count].len++;
        }
        cout << "Case " << t << ": " << clickBox(, count, ) << endl;
    }
    return ;
}