C++ code：prime decision

1 判断一个数是否为素数

对于判断一个数m是否为素数，最朴素的方式是按照素数的定义，试除以从2开始到m-1的整数，倘若无一例外地不能整除，则该数必为素数。

 #include<iostream>
 using namespace std;
 int main()
 {
     cout << "Please input a number:\n";
     int m;
     cin >> m;
     for (int i = ; i < m;++i)//i从2到m-1
     　　if (m%i == )
     　　{
         　　cout << m << " is not a prime.\n";
         　　return ;
     　　}
     cout << m << " is a prime.\n";
     cin.get();
     return ;

 }

下面来深究一下：

在数学上，假定某个整数m不是素数，则一定可以表示成两个因子的积：

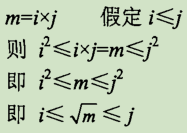
所以必定有一个因子不大于m的平方根（即这里所说的 i）。故判断m是否为素数，只要试除到m的平方根就可以了，不必一直到m-1（这段话请务必理解）。因此，上面的程序可以修改为：

 #include<iostream>
 #include<cmath>
 using namespace std;
 int main()
 {
     cout << "Please input a number:\n";
     int m;
     cin >> m;
     double sqrtm = sqrt(m*1.0);// 注意：这里的m*1.0是为了将int类型的m转化为适合开根号的浮点型数据。
     for (int i = ; i < sqrtm; ++i)
     if (m%i == )
     {
         cout << m << " is not a prime.\n";
         return ;
     }
     cout << m << " is a prime.\n";
     cin.get();
     return ;
 }

这里取了一个浮点型（double）变量sqrtm，其值为m的平方根，该值是调用了一个C++的库函数sqrt而得，它在cmath中说明。由于i是整数，所以不等式i<=sqrtm中，i只能取小于或等于sqrtm的最大整数。

修改后的程序，效率提高了一些。例如判断101是否为素数，本来要从2试除到100，现在只要从2试除到10就行了。