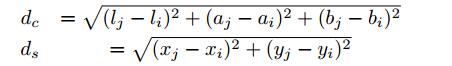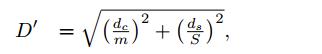SILC超像素分割算法详解(附Python代码)

SILC算法详解

一、原理介绍

SLIC算法是simple linear iterative cluster的简称，该算法用来生成超像素（superpixel）

算法步骤：

• 已知一副图像大小M*N,可以从RGB空间转换为LAB空间，LAB颜色空间表现的颜色更全面

• 假如预定义参数K，K为预生成的超像素数量，即预计将M*N大小的图像(像素数目即为M*N)分隔为K个超像素块，每个超像素块范围大小包含[（M*N）/K]个像素

• 假设每个超像素区域长和宽都均匀分布的话，那么每个超像素块的长和宽均可定义为S，S=sqrt(M*N/K)

• 遍历操作，将每个像素块的中心点的坐标(x,y)及其lab的值保存起来，加入到事先定义好的集合中

• 每个像素块的中心点默认是(S/2,S/2)进行获取的，有可能落在噪音点或者像素边缘（所谓像素边缘，即指像素突变处，比如从黑色过渡到白色的交界处），这里，利用差分方式进行梯度计算，调整中心点：

算法中，使用中心点的8领域像素点，计算获得最小梯度值的像素点，并将其作为新的中心点，差分计算梯度的公式：

    Gradient(x,y)=dx(i,j) + dy(i,j);

    dx(i,j) = I(i+1,j) - I(i,j); 

    dy(i,j) = I(i,j+1) - I(i,j);

    遍历现中心点的8领域像素点，将其中计算得到最小Gradient值的像素点作为新的中心点

• 调整完中心点后即需要进行像素点的聚类操作

    通过聚类的方式迭代计算新的聚类中心；

    首先，需要借助K-means聚类算法，将像素点进行归类，通过变换的欧氏聚距离公式进行，公式如下（同时参考像素值和坐标值提取相似度）：
    
    

     通过两个参数m和S来协调两种距离的比例分配。参数S即是上面第③步计算得出的每个像素块的长度值，而参数M为LAB空间的距离可能最大值，其可取的范围建议为[1,40]

     为了节省时间，只遍历每个超像素块中心点周边的2S*2S区域内的像素点，计算该区域内每个像素点距离哪一个超像素块的中心点最近，并将其划分到其中；完成一次迭代后，重新计算每个超像素块的中心点坐标，并重新进行迭代（注：衡量效率和效果后一般选择迭代10次）

二、代码实现

 import math
 from skimage import io, color
 import numpy as np

 class Cluster(object):

     cluster_index = 1

     def __init__(self, row, col, l=0, a=0, b=0):
         self.update(row, col, l, a, b)
         self.pixels = []
         self.no = self.cluster_index
         Cluster.cluster_index += 1

     def update(self, row, col, l, a, b):
         self.row = row
         self.col = col
         self.l = l
         self.a = a
         self.b = b

 class SLICProcessor(object):
     @staticmethod
     def open_image(path):
         rgb = io.imread(path)
         lab_arr = color.rgb2lab(rgb)
         return lab_arr

     @staticmethod
     def save_lab_image(path, lab_arr):
         rgb_arr = color.lab2rgb(lab_arr)
         io.imsave(path, rgb_arr)

     def make_cluster(self, row, col):
         row=int(row)
         col=int(col)
         return Cluster(row, col,
                        self.data[row][col][0],
                        self.data[row][col][1],
                        self.data[row][col][2])

     def __init__(self, filename, K, M):
         self.K = K
         self.M = M

         self.data = self.open_image(filename)
         self.rows = self.data.shape[0]
         self.cols = self.data.shape[1]
         self.N = self.rows * self.cols
         self.S = int(math.sqrt(self.N / self.K))

         self.clusters = []
         self.label = {}
         self.dis = np.full((self.rows, self.cols), np.inf)

     def init_clusters(self):
         row = self.S / 2
         col = self.S / 2
         while row < self.rows:
             while col < self.cols:
                 self.clusters.append(self.make_cluster(row, col))
                 col+= self.S
             col = self.S / 2
             row += self.S

     def get_gradient(self, row, col):
         if col + 1 >= self.cols:
             col = self.cols - 2
         if row + 1 >= self.rows:
             row = self.rows - 2

         gradient = (self.data[row + 1][col][0] +self.data[row][col+1][0]-2*self.data[row][col][0])+ \
                    (self.data[row + 1][col][1] +self.data[row][col+1][1]-2*self.data[row][col][1]) + \
                    (self.data[row + 1][col][2] +self.data[row][col+1][2]-2*self.data[row][col][2])

         return gradient

     def move_clusters(self):
         for cluster in self.clusters:
             cluster_gradient = self.get_gradient(cluster.row, cluster.col)
             for dh in range(-1, 2):
                 for dw in range(-1, 2):
                     _row = cluster.row + dh
                     _col = cluster.col + dw
                     new_gradient = self.get_gradient(_row, _col)
                     if new_gradient < cluster_gradient:
                         cluster.update(_row, _col, self.data[_row][_col][0], self.data[_row][_col][1], self.data[_row][_col][2])
                         cluster_gradient = new_gradient

     def assignment(self):
         for cluster in self.clusters:
             for h in range(cluster.row - 2 * self.S, cluster.row + 2 * self.S):
                 if h < 0 or h >= self.rows: continue
                 for w in range(cluster.col - 2 * self.S, cluster.col + 2 * self.S):
                     if w < 0 or w >= self.cols: continue
                     L, A, B = self.data[h][w]
                     Dc = math.sqrt(
                         math.pow(L - cluster.l, 2) +
                         math.pow(A - cluster.a, 2) +
                         math.pow(B - cluster.b, 2))
                     Ds = math.sqrt(
                         math.pow(h - cluster.row, 2) +
                         math.pow(w - cluster.col, 2))
                     D = math.sqrt(math.pow(Dc / self.M, 2) + math.pow(Ds / self.S, 2))
                     if D < self.dis[h][w]:
                         if (h, w) not in self.label:
                             self.label[(h, w)] = cluster
                             cluster.pixels.append((h, w))
                         else:
                             self.label[(h, w)].pixels.remove((h, w))
                             self.label[(h, w)] = cluster
                             cluster.pixels.append((h, w))
                         self.dis[h][w] = D

     def update_cluster(self):
         for cluster in self.clusters:
             sum_h = sum_w = number = 0
             for p in cluster.pixels:
                 sum_h += p[0]
                 sum_w += p[1]
                 number += 1
                 _h =int( sum_h / number)
                 _w =int( sum_w / number)
                 cluster.update(_h, _w, self.data[_h][_w][0], self.data[_h][_w][1], self.data[_h][_w][2])

     def save_current_image(self, name):
         image_arr = np.copy(self.data)
         for cluster in self.clusters:
             for p in cluster.pixels:
                 image_arr[p[0]][p[1]][0] = cluster.l
                 image_arr[p[0]][p[1]][1] = cluster.a
                 image_arr[p[0]][p[1]][2] = cluster.b
             image_arr[cluster.row][cluster.col][0] = 0
             image_arr[cluster.row][cluster.col][1] = 0
             image_arr[cluster.row][cluster.col][2] = 0
         self.save_lab_image(name, image_arr)

     def iterates(self):
         self.init_clusters()
         self.move_clusters()
         #考虑到效率和效果，折中选择迭代10次
         for i in range(10):
             self.assignment()
             self.update_cluster()
         self.save_current_image("output.jpg")

 if __name__ == '__main__':
     p = SLICProcessor('beauty.jpg', 200, 40)
     p.iterates()

三、运行效果截图

                         （原图）


                       （效果图）

代码参考了https://github.com/laixintao/slic-python-implementation，且做了改进

作为一枚技术小白，写这篇笔记的时候参考了很多博客论文，在这里表示感谢，转载请注明出处......