[洛谷P2123]皇后游戏

很抱歉，这个题我做的解法不是正解，只是恰巧卡了数据

目前数据已经更新，这个题打算过一段时间再去写。

目前在学习DP，这个会暂时放一放，很抱歉

这个题是一个国王游戏的变形(国王游戏就把我虐了qwq)

题目背景

还记得 NOIP 2012 提高组 Day1 的国王游戏吗？时光飞逝，光阴荏苒，两年

过去了。国王游戏早已过时，如今已被皇后游戏取代，请你来解决类似于国王游

戏的另一个问题。

题目描述

皇后有 n 位大臣，每位大臣的左右手上面分别写上了一个正整数。恰逢国庆

节来临，皇后决定为 n 位大臣颁发奖金，其中第 i 位大臣所获得的奖金数目为第

i－1 位大臣所获得奖金数目与前 i 位大臣左手上的数的和的较大值再加上第 i 位

大臣右手上的数。

形式化地讲：我们设第 i 位大臣左手上的正整数为 ai，右手上的正整数为 bi，

则第 i 位大臣获得的奖金数目为 ci可以表达为：

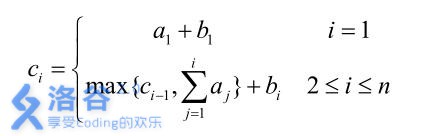
当然，吝啬的皇后并不希望太多的奖金被发给大臣，所以她想请你来重新安

排一下队伍的顺序，使得获得奖金最多的大臣，所获奖金数目尽可能的少。

注意：重新安排队伍并不意味着一定要打乱顺序，我们允许不改变任何一

位大臣的位置。

输入输出格式

输入格式：

第一行包含一个正整数 T，表示测试数据的组数。

接下来 T 个部分，每个部分的第一行包含一个正整数 n，表示大臣的数目。

每个部分接下来 n 行中，每行两个正整数，分别为 ai和 bi，含义如上文所述。

输出格式：

共 T 行，每行包含一个整数，表示获得奖金最多的大臣所获得的奖金数目

输入输出样例：

输入

输出

分析

这道题贪心做法的正确性显然，只需要将题目所给你的式子算的过程中加一个贪心排序就可以做了。

(国王游戏要高精，但这个题我貌似long long水过了？！)

Codes:

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define ll long long
using namespace std;
ll n,T,sum;
ll C[];
struct Node
{
    int left;
    int right;
    bool operator < (const Node &rt) const {
        return min(left,rt.right) < min(right,rt.left);  //重载运算符，注意这里是用min的
    }
}node[];
inline int read()  //快读
{
    int x=,f=;
    char ch=getchar();
    while(ch<'' || ch>'')
    {
        if(ch == '-')
        f = -;
        ch=getchar();
    }
    while(ch >= '' && ch <= '')
    {
        x = x *  + ch - '';
        ch = getchar();
    }
    return x * f;
}
int main()
{
    T = read();  //输入数据组数
    while(T--)
    {
        memset(C,,sizeof(C));  //清空数组
        n = read();
        for(int i=;i<=n;i++)
        {
            node[i].left = read();
            node[i].right = read();
        }
        sort(node + ,node + n + );  //已经重置好了，直接判断就行
        sum = ;  //别忘了要重置
        for(int i=;i<=n;i++)
        {
            sum += node[i].left;  //以中间变量sum来存储一个运算时候的变量，也保证了时时更新
            C[i] = max(C[i - ],sum) + node[i].right;  //题目所描述的
        }
        printf("%lld\n",C[n]);  //输出
    }
    return ;
}

完结撒花qwq