[la P4487] Exclusive-OR

[la P4487] Exclusive-OR

Time limit 3000 ms  OS Linux

You are not given n non-negative integers X0, X1, . . . , Xn−1 less than 220, but they do exist, and their values never change.

I’ll gradually provide you some facts about them, and ask you some questions.

There are two kinds of facts, plus one kind of question:

Format Meaning

I p v I tell you Xp = v

I p q v I tell you Xp XOR Xq = v

Q k p1 p2 . . . pk Please tell me the value of Xp1 XOR Xp2 XOR . . . XOR Xpk

Input

There will be at most 10 test cases. Each case begins with two integers n and Q (1 ≤ n ≤ 20, 000, 2 ≤ Q ≤ 40, 000). Each of the following lines

contains either a fact or a question, formatted as stated above.

The k parameter in the questions will be a positive integer not greater than 15, and the v parameter in the facts will be a non-negative integer less

than 220. The last case is followed by n = Q = 0, which should not be processed.

Output

For each test case, print the case number on its own line, then the answers, one on each one. If you can’t deduce the answer for a particular

question, from the facts I provide you before that question, print ‘I don’t know.’, without quotes. If the i-th fact (don’t count questions) cannot

be consistent with all the facts before that, print ‘The first i facts are conflicting.’, then keep silence for everything after that (including

facts and questions).

Print a blank line after the output of each test case.

Sample Input
2 6
I 0 1 3
Q 1 0
Q 2 1 0
I 0 2
Q 1 1
Q 1 0
3 3
I 0 1 6
I 0 2 2
Q 2 1 2
2 4
I 0 1 7
Q 2 0 1
I 0 1 8
Q 2 0 1
0 0

Sample Output
Case 1:
I don’t know.
3
1
2
Case 2:
4
Case 3:
7
The first 2 facts are conflicting.

很好的一道题目！大力推荐，只是如果认真做，有可能会续掉很长时间。

题目的意思是，给你一系列的操作，有3种形式：

1.I p v 告诉我们Xp=v

2.I p q v 告诉我们Xp^Xq=v

3.Q k p1 p2 ... pk 问我们 Xp1^Xp2^...^Xpk的值。

当然，如果在某个1或2操作时，我们得到的信息与我们已知信息冲突，输出在第几条信息（不包括询问）产生矛盾。

对于每个询问，如果并不能确定答案，输出I don't know.

好的，当我们读懂题目后，就可以思考了。

想一想，这和什么算法或数据结构有关联呢？

这一题我们采用并查集（加权）。

其实我原来想的已经很像正解了，但是由于没有想到“Q”操作，然后就GG了。

好的，我们来讲讲这题怎么用的并查集。

我们用fa[i]表示i的父亲，sum[i]表示从i到i所在的树的根节点，每个点的X值的xor值。

为了便于判断，我们刻意加上一个超级点——0。0的值已知，为0。刚开始的时候，所有节点的父亲都是自己，值未知（为了方便仍设为0）。

则对于1操作：

先判断是否矛盾。怎么样是矛盾的？仅当p的祖先是0时有可能，还要考虑权值。

首先，我们会（或是必要的）进行路径压缩，此时，sum[p]已经更新了，由于fa[p]=0，X[0]=0，所以x[p]=sum[p]。

也就是说，getfa(p)一遍（同时进行路径压缩并正确更新sum），判断v==sum[p]就好了。

如果原来不知道这个信息，则合并fa[p]和0。注意0永远要是一棵树的根节点。

这样的话，sum[getfa(p)]就是sum[p]^v了。

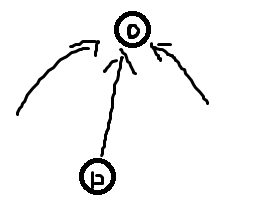
对于操作2，相当于一棵树中的判断或两颗树的合并。

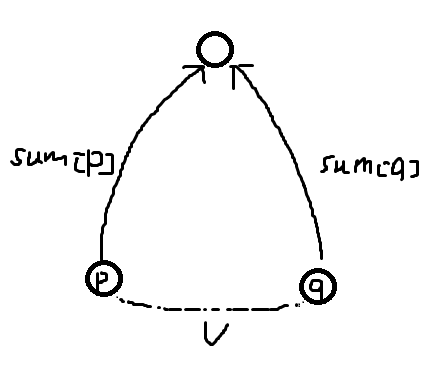
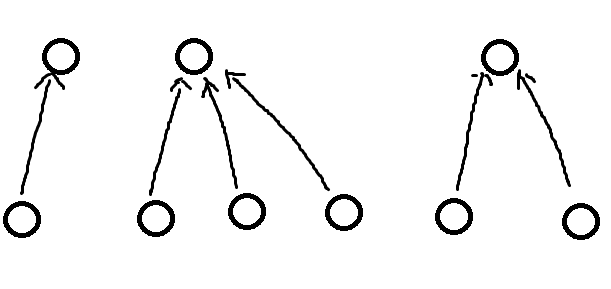
判断的图：

下面p和q的连线可以看做是有向的，不管是上面方向，都应该有sum[p]^sum[q]==v，这就是判断。

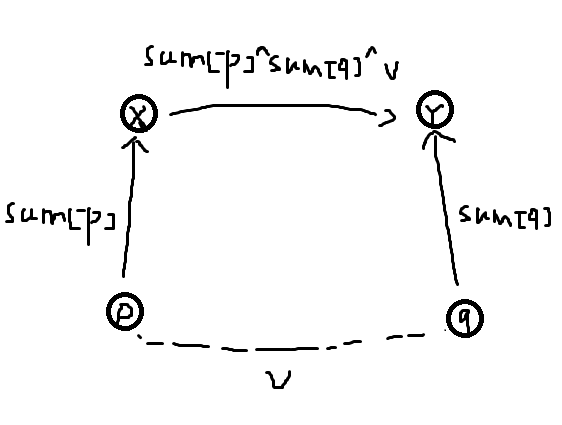
合并操作：

应该很明显了吧，用的就是xor的性质，因为sum[q]=v^sum[p]^sum[x]，所以sum[x]=sum[p]^sum[q]^v。

注意x不能为0，为0了就和y点swap一下，不可能同时x==0且y==0。

稍微要动一下脑袋的就是“Q”操作。

我们知道，这些给出的点可能是在不同的树里面，但这并不代表不能算出来。

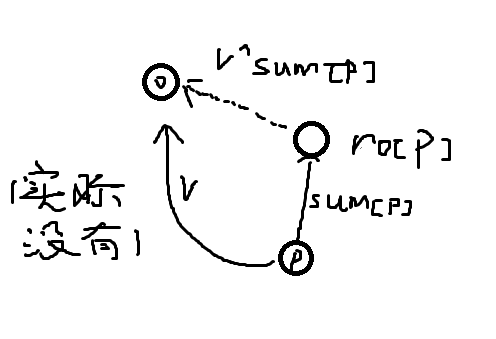
当我们路径压缩后会是这种情况：

这些点的父节点就是根节点，所以不进行区分，就直接说父节点好了。有些点的父节点可能是自己，也可能是其他，还有可能是0。

我们可以把询问的答案变成：

sum[p1]^sum[fa[p1]]^sum[p2]^sum[fa[p2]]^sum[p3]^sum[fa[p3]]^...

那么，由于每一棵树的根节点（除0外）的sum都是0，也就是不知道其权值。

但是，根据xor的性质，一个数xor偶数次就消去了。所以我们判断一下所有非0的fa[px]出现的次数到底是奇数次还是偶数次。

当且仅当出现偶数次，是有解的，解就是sum[p1]^sum[p2]^sum[p3]^...，否则就是I don't know.了。

再注意一下，正确的getfa应该长这样：

 inline int get(int x) {
     if (fa[x]==x) {
         return x;
     }
     int p=fa[x];
     fa[x]=get(fa[x]);
     sum[x]^=sum[p];
     return fa[x];
 }

还有一点，就是把告诉你单点值那个操作归到第2种也是可以的，注意一下无论何时，根为0就行了。

code 1：

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <iostream>
 ;
 int n,q,len,fa[N],ew[N];
 ],ero,fac,ans,tag;
 ]; bool cnt[N];
 void read() {
     gets(s),len=strlen(s);
     num[]=;
     ; i<len; ++i) {
         ') {
             num[++num[]]=;
         }
         else {
             num[num[]]=num[num[]]*+s[i]-';
         }
     }
     ]=='I') {
         ++fac;
         ]==) {
             ++num[];
         }
         else {
             ++num[]; ++num[];
         }
     }
     else {
         ; i<=num[]; ++i) {
             ++num[i];
         }
     }
 }
 inline int get(int x) {
     if (fa[x]==x) {
         return x;
     }
     int p=fa[x];
     fa[x]=get(fa[x]);
     ew[x]^=ew[p];
     return fa[x];
 }
 int main() {
     ;
     while (scanf("%d%d",&n,&q)!=EOF,n||q) {
         printf(,fac=;
         ; i<=n+; i++) {
             fa[i]=i; ew[i]=;
         }
         fa[]=; ew[]=;
         getchar();
         ; cq<=q; ++cq) {
             read();
             if (ero) {
                 continue;
             }
             ]=='I') {
                 ]==) {
                     x=]);
                     &&ew[num[]]!=num[]) {
                         ero=;
                         printf("The first %d facts are conflicting.\n",fac);
                     }
                     else {
                         x=]);
                         fa[x]=; ew[x]=ew[num[]]^num[];
                     }
                     continue;
                 }
                 x=]),y=]);
                 if (x==y) {
                     ]]^ew[num[]])!=num[]) {
                         ero=;
                         printf("The first %d facts are conflicting.\n",fac);
                     }
                     continue;
                 }
                 ) {
                     std::swap(num[],num[]);
                     std::swap(x,y);
                 }
                 fa[y]=x; ew[y]=ew[num[]]^ew[num[]]^num[];
             }
             else
             ]=='Q') {
                 ans=; tag=;
                 ; i<=num[]; ++i) {
                     x=get(num[i]);
                     ans^=ew[num[i]];
                     num[i]=x;
                     cnt[x]^=;
                 }
                 ; i<=num[]; ++i) {
                     ) {
                         tag=;
                         break;
                     }
                 }
                 ; i<=num[]; ++i) {
                     cnt[num[i]]=;
                 }
                 if (tag) {
                     printf("I don't know.\n");
                 }
                 else {
                     printf("%d\n",ans);
                 }
             }
         }
         putchar('\n');
     }
     ;
 }

code 2：（稍微排布好看了一点qwq）

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <iostream>
 ;
 int n,q,len,fa[N],sum[N];
 ],ero,fac;
 ]; bool cnt[N];
 void init() {
     gets(s); len=strlen(s); num[]=;
     ; i<len; ++i) {
         ') {
             num[++num[]]=;
         }
         else {
             num[num[]]=num[num[]]*+s[i]-';
         }
     }
     ]=='I') {
         ++fac;
         ]==) {
             num[]=num[]; num[]=++num[]; num[]=;
         }
         else {
             ++num[]; ++num[];
         }
     }else
     ]=='Q') {
         ; i<=num[]; ++i) {
             ++num[i];
         }
     }
 }
 inline int get(int x) {
     if (fa[x]==x) {
         return x;
     }
     int p=fa[x];
     fa[x]=get(fa[x]);
     sum[x]^=sum[p];
     return fa[x];
 }
 int main() {
     ;
     while (scanf("%d%d",&n,&q),n||q) {
         printf("Case %d:\n",++cas);
         fac=; ero=;
         ; i<=n; ++i) {
             fa[i]=i; sum[i]=;
         }
         getchar();
         for (; q; --q) {
             init();
             if (ero) continue;
             ]=='I') {
                 x=]); y=]);
                 ]]^sum[num[]])!=num[]) {
                     ero=;
                     printf("The first %d facts are conflicting.\n",fac);
                     continue;
                 }
                 ) {
                     std::swap(x,y);
                     std::swap(num[],num[]);
                 }
                 fa[y]=x; sum[y]=sum[num[]]^sum[num[]]^num[];
             }else
             ]=='Q') {
                 ans=; tag=;
                 ; i<=num[]; ++i) {
                     x=get(num[i]);
                     ans^=sum[num[i]];
                     num[i]=x;
                     cnt[x]^=;
                 }
                 ; i<=num[]; ++i) {
                     if (cnt[num[i]]&&num[i]) {
                         tag=;
                         break;
                     }
                 }
                 ; i<=num[]; ++i) {
                     cnt[num[i]]=;
                 }
                 if (tag) {
                     printf("I don't know.\n");
                 }
                 else {
                     printf("%d\n",ans);
                 }
             }
         }
         putchar('\n');
     }
     ;
 }