使用 C# 代码实现拓扑排序
0.参考资料
尊重他人的劳动成果,贴上参考的资料地址,本文仅作学习记录之用。
- https://www.codeproject.com/Articles/869059/Topological-sorting-in-Csharp
- https://songlee24.github.io/2015/05/07/topological-sorting/
- https://www.cnblogs.com/skywang12345/p/3711483.html
1.介绍
自己之前并没有接触过拓扑排序,顶多听说过拓扑图。在写前一篇文章的时候,看到 Abp 框架在处理模块依赖项的时候使用了拓扑排序,来确保顶级节点始终是最先进行加载的。第一次看到觉得很神奇,看了一下维基百科头也是略微大,自己的水平也是停留在冒泡排序的层次。ヽ(≧□≦)ノ
看了第二篇参考资料才大致了解,在此记录一下。
2.原理
先来一个基本定义:
在图论中,拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列。且该序列必须满足下面两个条件:
- 每个顶点出现且只出现一次。
- 若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。
有向无环图(DAG)才有拓扑排序,非DAG图没有拓扑排序一说。
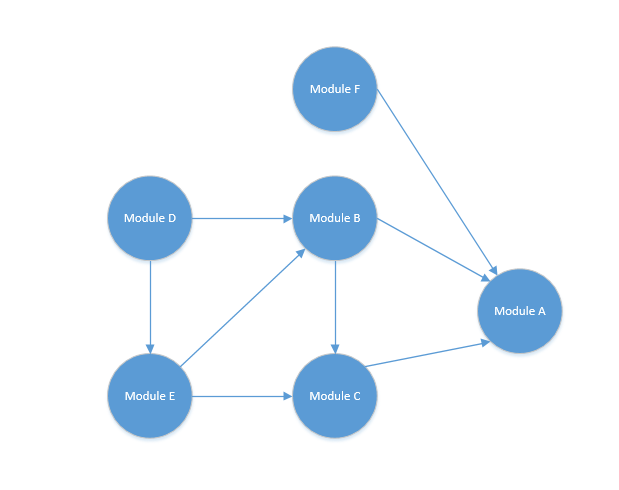
例如,有一个集合它的依赖关系如下图:
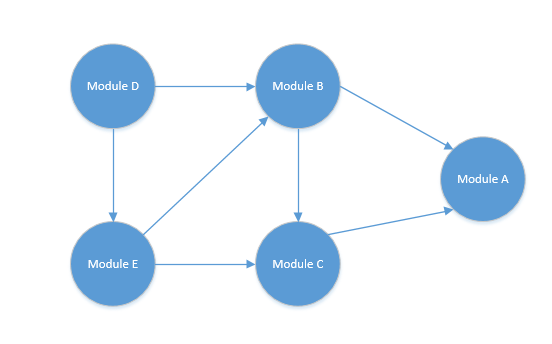
可以看到他有一个依赖关系:
- Module D 依赖于 Module E 与 Module B 。
- Module E 依赖于 Module B 与 Module C 。
- Module B 依赖于 Module A 与 Module C 。
- Module C 依赖于 Module A 。
- Module A 无依赖 。
这个就是一个 DAG 图,我们要得到它的拓扑排序,一个简单的步骤如下:
- 从 DAG 图中选择一个没有前驱的顶点并输出。
- 从 DAG 图中删除该顶点,以及以它为起点的有向边。
- 重复步骤 1、2 直到当前的 DAG 图为空,或者当前图不存在无前驱的顶点为止。
按照以上步骤,我们来进行一个排序试试。
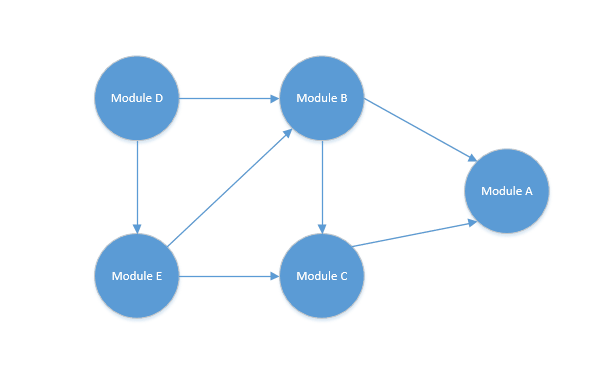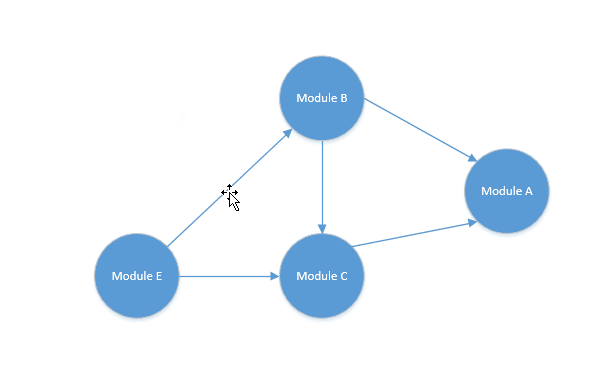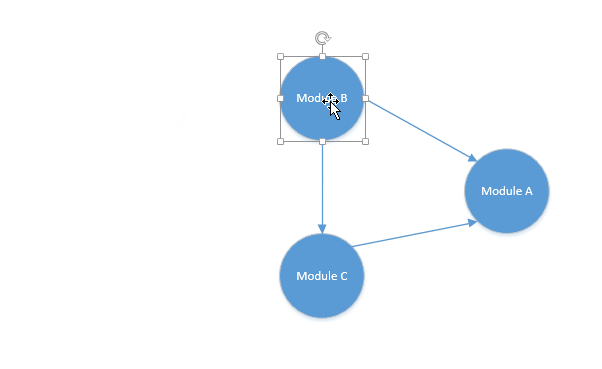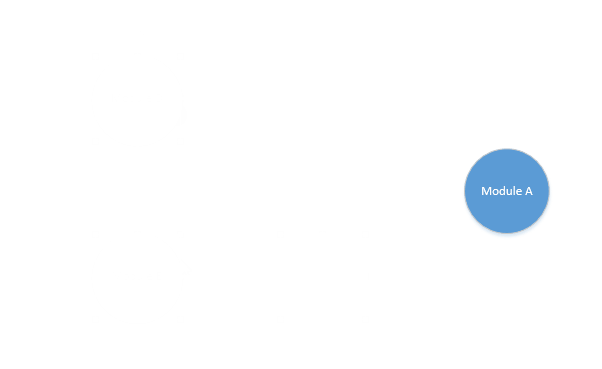
最后的排序结果就是:
Module D -> Module E -> Module B -> Module C -> Module A
emmmm,其实一个有向无环图可以有一个或者多个拓扑序列的,因为有的时候会存在一种情况,即以下这种情况:
这个时候你就可能会有这两种结果
D->E->B->C->F->A
D->E->B->F->C->A
因为 F 与 C 是平级的,他们初始化顺序即便不同也没有什么影响,因为他们的依赖层级是一致的,不过细心的朋友可能会发现这个顺序好像是反的,我们还需要将其再反转一次。
3.实现
上面这种方法仅适用于已知入度的时候,也就是说这些内容本身就是存在于一个有向无环图之中的,如果按照以上方法进行拓扑排序,你需要维护一个入度为 0 的队列,然后每次迭代移除入度为 0 顶点所指向的顶点入度。
例如有以下图:
按照我们之前的算法,
- 首先初始化队列,将 5 与 4 这两个入度为 0 的顶点加入队列当中。
- 执行 While 循环,条件是队列不为空。
- 之后首先拿出 4 。
- 然后针对其指向的顶点 0 与 顶点 1 的入度减去 1。
- 减去指向顶点入度的时候同时判断,被减去入度的顶点其值是否为 0 。
- 这里 1 入度被减去 1 ,为 0 ,添加到队列。
- 0 顶点入度减去 1 ,为 1。
- 队列现在有 5 与 1 这两个顶点,循环判断队列不为空。
- 5 指向的顶点 0 入度 减去 1,顶点 0 入度为 0 ,插入队列。
这样反复循环,最终队列全部清空,退出循环,得到拓扑排序的结果4, 5, 2, 0, 3, 1 。
4.深度优先搜索实现
在参考资料 1 的代码当中使用的是深度优先算法,它适用于有向无环图。
有以下有向环图 G2:

对上图 G2 进行深度优先遍历,首先从入度为 0 的顶点 A 开始遍历:
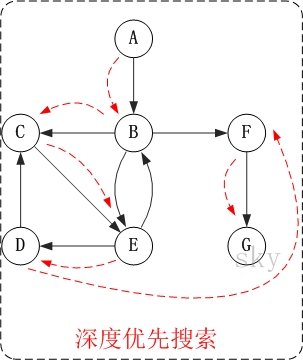
它的步骤如下:
访问 A 。
访问 B 。
访问 C 。
在访问了 B 后应该是访问 B 的另外一个顶点,这里可以是随机的也可以是有序的,具体取决于你存储的序列顺序,这里先访问 C 。
访问 E 。
访问 D 。
这里访问 D 是因为 B 已经被访问过了,所以访问顶点 D 。
访问 F 。
因为顶点 C 已经被访问过,所以应该回溯访问顶点 B 的另一个有向边指向的顶点 F 。
访问 G 。
因此最后的访问顺序就是 A -> B -> C -> E -> D -> F -> G ,注意顺序还是不太对哦。
看起来跟之前的方法差不多,实现当中,其 Sort() 方法内部包含一个 visited 字典,用于标记已经访问过的顶点,sorted 则是已经排序完成的集合列表。
在字典里 Key 是顶点的值,其 value 值用来标识是否已经访问完所有路径,为 true 则表示正在处理该顶点,为 false 则表示已经处理完成。
现在我们来写实现吧:
public static IList<T> Sort<T>(IEnumerable<T> source, Func<T, IEnumerable<T>> getDependencies)
{
var sorted = new List<T>();
var visited = new Dictionary<T, bool>();
foreach (var item in source)
{
Visit(item, getDependencies, sorted, visited);
}
return sorted;
}
public static void Visit<T>(T item, Func<T, IEnumerable<T>> getDependencies, List<T> sorted, Dictionary<T, bool> visited)
{
bool inProcess;
var alreadyVisited = visited.TryGetValue(item, out inProcess);
// 如果已经访问该顶点,则直接返回
if (alreadyVisited)
{
// 如果处理的为当前节点,则说明存在循环引用
if (inProcess)
{
throw new ArgumentException("Cyclic dependency found.");
}
}
else
{
// 正在处理当前顶点
visited[item] = true;
// 获得所有依赖项
var dependencies = getDependencies(item);
// 如果依赖项集合不为空,遍历访问其依赖节点
if (dependencies != null)
{
foreach (var dependency in dependencies)
{
// 递归遍历访问
Visit(dependency, getDependencies, sorted, visited);
}
}
// 处理完成置为 false
visited[item] = false;
sorted.Add(item);
}
}
顶点定义:
// Item 定义
public class Item
{
// 条目名称
public string Name { get; private set; }
// 依赖项
public Item[] Dependencies { get; set; }
public Item(string name, params Item[] dependencies)
{
Name = name;
Dependencies = dependencies;
}
public override string ToString()
{
return Name;
}
}
调用:
static void Main(string[] args)
{
var moduleA = new Item("Module A");
var moduleC = new Item("Module C", moduleA);
var moduleB = new Item("Module B", moduleC);
var moduleE = new Item("Module E", moduleB);
var moduleD = new Item("Module D", moduleE);
var unsorted = new[] { moduleE, moduleA, moduleD, moduleB, moduleC };
var sorted = Sort(unsorted, x => x.Dependencies);
foreach (var item in sorted)
{
Console.WriteLine(item.Name);
}
Console.ReadLine();
}
结果:
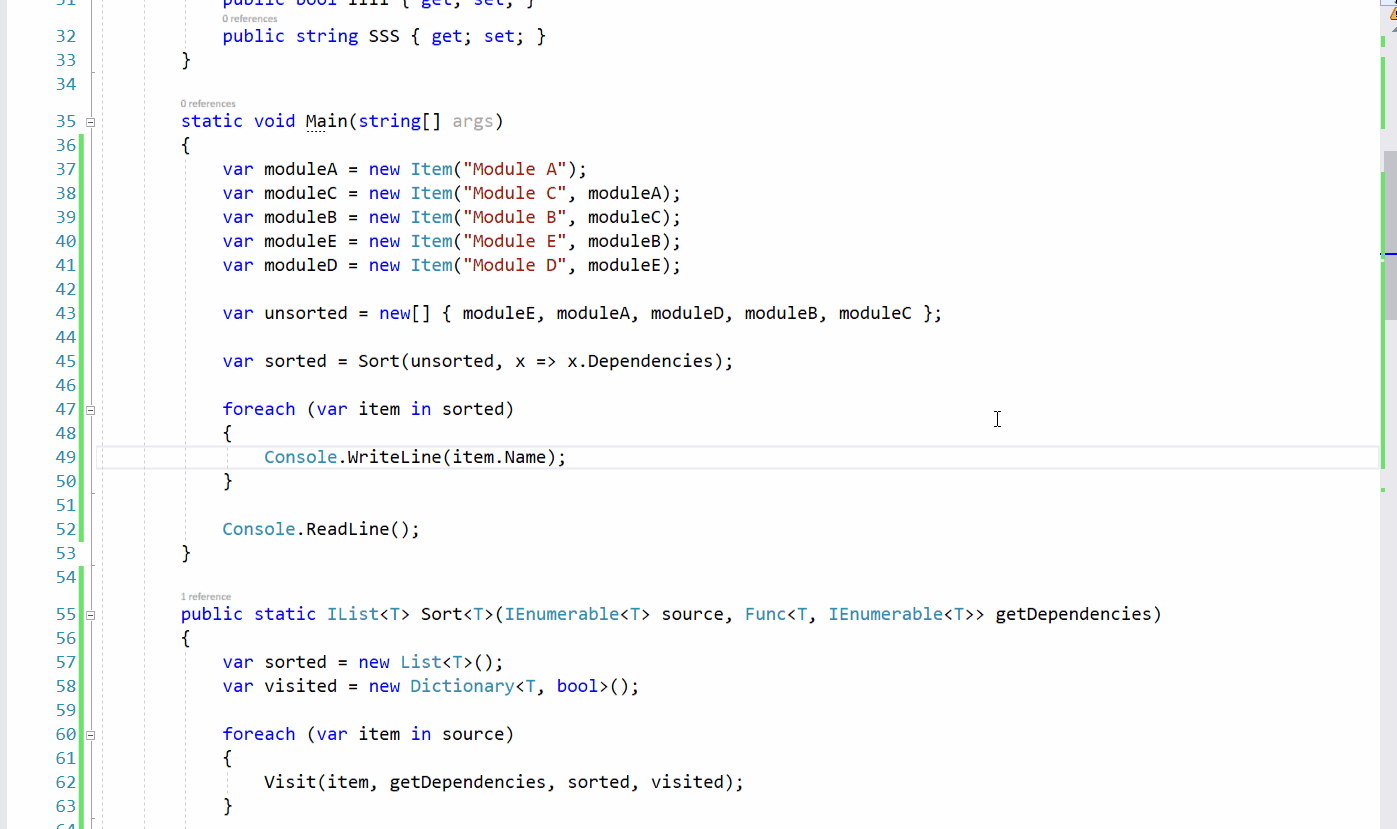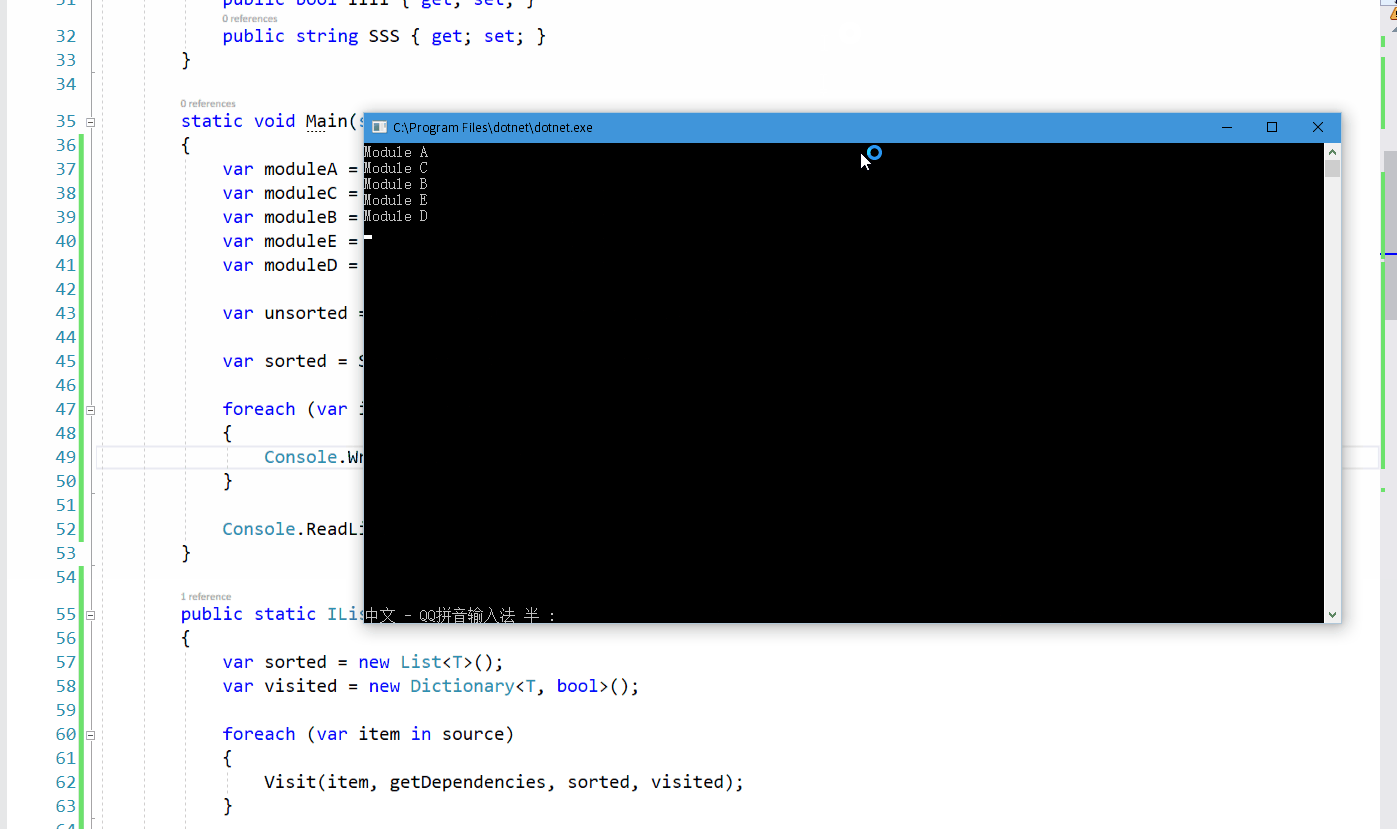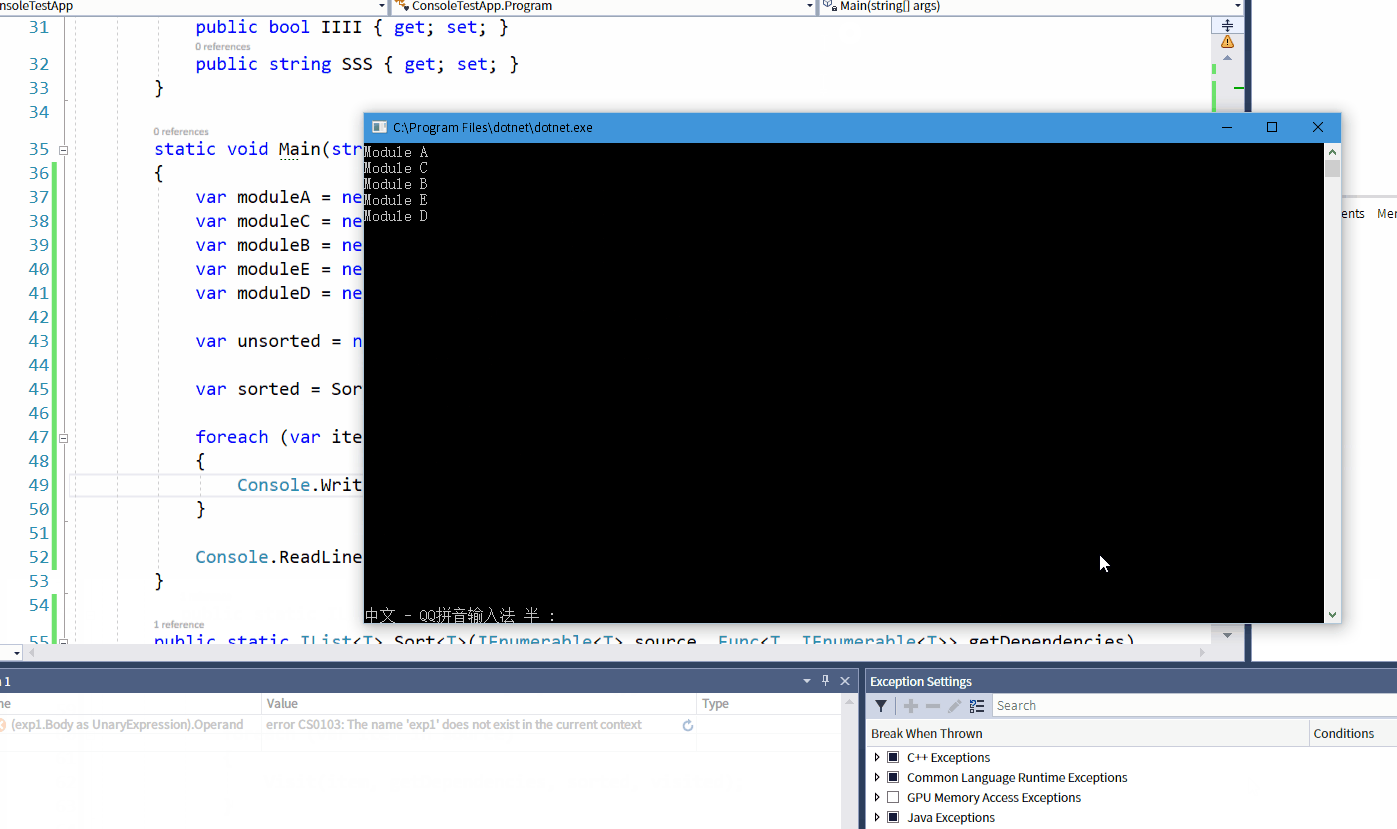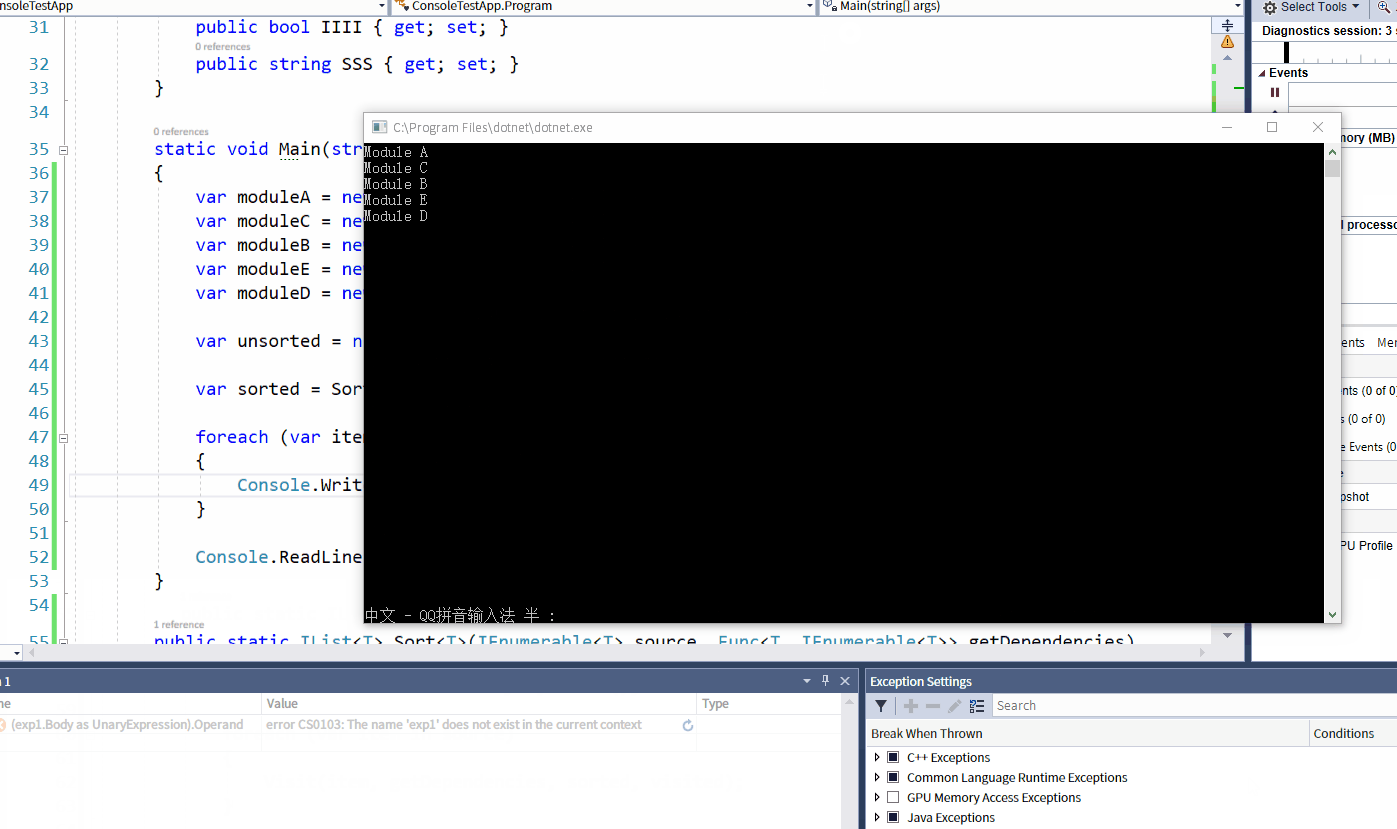
使用 C# 代码实现拓扑排序的更多相关文章
- [C#]使用 C# 代码实现拓扑排序 dotNet Core WEB程序使用 Nginx反向代理 C#里面获得应用程序的当前路径 关于Nginx设置端口号,在Asp.net 获取不到的,解决办法 .Net程序员 初学Ubuntu ,配置Nignix 夜深了,写了个JQuery的省市区三级级联效果
[C#]使用 C# 代码实现拓扑排序 目录 0.参考资料 1.介绍 2.原理 3.实现 4.深度优先搜索实现 回到顶部 0.参考资料 尊重他人的劳动成果,贴上参考的资料地址,本文仅作学习记录之用. ...
- *HDU1285 拓扑排序
确定比赛名次 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Subm ...
- 拓扑排序(三)之 Java详解
前面分别介绍了拓扑排序的C和C++实现,本文通过Java实现拓扑排序. 目录 1. 拓扑排序介绍 2. 拓扑排序的算法图解 3. 拓扑排序的代码说明 4. 拓扑排序的完整源码和测试程序 转载请注明出处 ...
- 拓扑排序(二)之 C++详解
本章是通过C++实现拓扑排序. 目录 1. 拓扑排序介绍 2. 拓扑排序的算法图解 3. 拓扑排序的代码说明 4. 拓扑排序的完整源码和测试程序 转载请注明出处:http://www.cnblogs. ...
- 拓扑排序(一)之 C语言详解
本章介绍图的拓扑排序.和以往一样,本文会先对拓扑排序的理论知识进行介绍,然后给出C语言的实现.后续再分别给出C++和Java版本的实现. 目录 1. 拓扑排序介绍 2. 拓扑排序的算法图解 3. 拓扑 ...
- 算法与数据结构(七) AOV网的拓扑排序
今天博客的内容依然与图有关,今天博客的主题是关于拓扑排序的.拓扑排序是基于AOV网的,关于AOV网的概念,我想引用下方这句话来介绍: AOV网:在现代化管理中,人们常用有向图来描述和分析一项工程的计划 ...
- 【BZOJ-2938】病毒 Trie图 + 拓扑排序
2938: [Poi2000]病毒 Time Limit: 1 Sec Memory Limit: 128 MBSubmit: 609 Solved: 318[Submit][Status][Di ...
- BZOJ1565 [NOI2009]植物大战僵尸(拓扑排序 + 最大权闭合子图)
题目 Source http://www.lydsy.com/JudgeOnline/problem.php?id=1565 Description Input Output 仅包含一个整数,表示可以 ...
- 拓扑排序&&欧拉(回)路
摘要:最近是不适合写代码么?忘记初始化wa到死<_=_=_>.唔--最近在学习图论,从基础搞起,先搞了拓扑排序和欧拉(回)路. Part 0. 拓扑排序 ==挖坑== Part 1. 欧拉 ...
随机推荐
- 编写一份好的 Vimrc
编写一份好的 Vimrc 目录 如何 Vimrc 色彩 空白字符与制表符 UI 配置 搜索 折叠 移动 用户自定义的前缀快捷按键 插件CtrlP 启动配置 终端Tmux 自动命令及其分组 备份 自定义 ...
- CyclicBarrier介绍
应用场景 在某种需求中,比如一个大型的任务,常常需要分配好多子任务去执行,只有当所有子任务都执行完成时候,才能执行主任务,这时候,就可以选择CyclicBarrier了. 实例分析 我们需要统计全国的 ...
- mybatis中有趣的符号#与$
${ }是字符串替换,相当于直接显示数据,#{ }是预编译处理,相当于对数据加上双引号 即#是将传入的值当做字符串的形式,先替换为?号,然后调用PreparedStatement的set方法来赋值,而 ...
- 2018-2019-1 20189201 《LInux内核原理与分析》第九周作业
那一天我二十一岁,在我一生的黄金时代.我有好多奢望.我想爱,想吃,还想在一瞬间变成天上半明半暗的云.那一年我二十一岁,在我一生的黄金时代.我有好多想法.我思索,想象,我不知该如何行动,我想知道一个城市 ...
- Ubuntu安装MySQL和Python库MySQLdb步骤
一.安装MySQL服务器和客户端 执行以下命令: sudo apt-get install mysql-server-5.6 mysql-client-5.6 sudo apt-get install ...
- 微信小程序之微信登陆 —— 微信小程序教程系列(20)
简介: 微信登陆,在新建一个微信小程序Hello World项目的时候,就可以看到项目中出现了我们的微信头像,其实这个Hello World项目,就有一个简化版的微信登陆.只不过是,还没有写入到咱们自 ...
- css 制作导航条布局
代码: <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8 ...
- ajax(2)
AJAX全称: Asynchronous JavaScript and XML ( 异步的JavaScript 和 XML) Ajax的本质就是:XMLHttpRequest 对象: 案例: v ...
- C语言表达式和语句
一.表达式 在C语言中,常量.变量.函数调用以及按C语言语法规则用运算符把运算数连接起来的式子都是合法的表达式 . 最后一类可以理解为运算符和运算对象的组合.例如: 算术表达式 = 算术运算符 + 运 ...
- [LeetCode] Exam Room 考试房间
In an exam room, there are N seats in a single row, numbered 0, 1, 2, ..., N-1. When a student enter ...

