POJ 1966 Cable TV Network

Cable TV Network

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 4702		Accepted: 2173

Description

The interconnection of the relays in a cable TV network is bi-directional. The network is connected if there is at least one interconnection path between each pair of relays present in the network. Otherwise the network is disconnected. An empty network or a network with a single relay is considered connected. The safety factor f of a network with n relays is: 
1. n, if the net remains connected regardless the number of relays removed from the net. 
2. The minimal number of relays that disconnect the network when removed.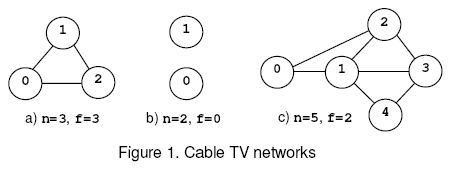 

For example, consider the nets from figure 1, where the circles mark the relays and the solid lines correspond to interconnection cables. The network (a) is connected regardless the number of relays that are removed and, according to rule (1), f=n=3. The network (b) is disconnected when 0 relays are removed, hence f=0 by rule (2). The network (c) is disconnected when the relays 1 and 2 or 1 and 3 are removed. The safety factor is 2.

Input

Write a program that reads several data sets from the standard input and computes the safety factor for the cable networks encoded by the data sets. Each data set starts with two integers: 0<=n<=50,the number of relays in the net, and m, the number of cables in the net. Follow m data pairs (u,v), u < v, where u and v are relay identifiers (integers in the range 0..n-1). The pair (u,v) designates the cable that interconnects the relays u and v. The pairs may occur in any order.Except the (u,v) pairs, which do not contain white spaces, white spaces can occur freely in input. Input data terminate with an end of file and are correct.

Output

For each data set, the program prints on the standard output, from the beginning of a line, the safety factor of the encoded net.

Sample Input

0 0
1 0
3 3 (0,1) (0,2) (1,2)
2 0
5 7 (0,1) (0,2) (1,3) (1,2) (1,4) (2,3) (3,4)

Sample Output

0
1
3
0
2

Hint

The first data set encodes an empty network, the second data set corresponds to a network with a single relay, and the following three data sets encode the nets shown in figure 1.

Source

Southeastern Europe 2004

[Submit]   [Go Back]   [Status]   [Discuss]

将原图中每个点拆成两个点，分别为入点和出点，从入点向出点连一条容量为1的边，代表割掉这个点的费用为1。

对于原图中的一条边(x,y)，连一条x的出点到y的入点容量为正无穷的边，以及一条y的出点到x的入点容量为正无穷的边。

枚举新图中的S和T，S在出点中枚举，T在入点中枚举，求最小割，更新答案。

 #include <cstdio>
 #include <cstring>

 const int inf = 2e9;
 const int maxn = ;

 inline int nextInt(void)
 {
     register int ret = ;
     register int neg = false;
     register int bit = getchar();

     for (; bit < ; bit = getchar())
         if (bit == '-')neg ^= true;

     for (; bit > ; bit = getchar())
         ret = ret *  + bit - ;

     return neg ? -ret : ret;
 }

 template <class T>
 inline T min(T a, T b)
 {
     return a < b ? a : b;
 }

 int n, m;
 int s, t;
 int edges;
 int hd[maxn];
 int nt[maxn];
 int to[maxn];
 int fl[maxn];
 int bp[maxn];

 inline void add(int u, int v, int f)
 {
     nt[edges] = hd[u]; to[edges] = v; fl[edges] = f; hd[u] = edges++;
     nt[edges] = hd[v]; to[edges] = u; fl[edges] = ; hd[v] = edges++;
 }

 int dep[maxn];

 inline bool bfs(void)
 {
     static int que[maxn];
     static int head, tail;

     memset(dep, , sizeof(dep));
     head = , tail = ;
     que[tail++] = s;
     dep[s] = ;

     while (head != tail)
     {
         int u = que[head++], v;
         for (int i = hd[u]; ~i; i = nt[i])
             if (!dep[v = to[i]] && fl[i])
                 dep[v] = dep[u] + , que[tail++] = v;
     }

     return dep[t];
 }

 int dfs(int u, int f)
 {
     if (u == t || !f)
         return f;

     int used = , flow, v;

     for (int i = hd[u]; ~i; i = nt[i])
         if (dep[v = to[i]] == dep[u] +  && fl[i])
         {
             flow = dfs(v, min(f - used, fl[i]));

             used += flow;
             fl[i] -= flow;
             fl[i^] += flow;

             if (used == f)
                 return f;
         }

     if (!used)
         dep[u] = ;

     return used;
 }

 inline int maxFlow(void)
 {
     int maxFlow = , newFlow;

     while (bfs())
         while (newFlow = dfs(s, inf))
             maxFlow += newFlow;

     return maxFlow;
 }

 signed main(void)
 {
     while (~scanf("%d%d", &n, &m))
     {
         memset(hd, -, sizeof(hd)), edges = ;

         for (int i = ; i <= m; ++i)
         {
             int u = nextInt();
             int v = nextInt();

             add(u << , v <<  | , inf);
             add(v << , u <<  | , inf);
         }

         for (int i = ; i < n; ++i)
             add(i <<  | , i << , );

         memcpy(bp, fl, sizeof(bp));

         int ans = inf;

         for (int i = ; i < n; ++i)
             for (int j = ; j < n; ++j)
                 if (i != j)
                 {
                     s = i << ;
                     t = j <<  | ;
                     memcpy(fl, bp, sizeof(fl));
                     ans = min(ans, maxFlow());
                 }

         printf("%d\n", ans == inf ? n : ans);
     }
 }

@Author: YouSiki