Day5 Numerical simulation of optical wave propagation之通过随机介质（如大气湍流）的传播（一）

一 分步光束传播方法

到目前为止，人们已经设计出传播算法，用于模拟通过真空和通过可用光线矩阵描述的简单光学系统的传播。

其中分步光束传播方法除了描述上述传播过程，还有更复杂的应用，包括：部分时间和空间相干光源、通过确定结构（如光纤）和集成光学设备的相干传播、通过随机介质（如大气湍流）的传播等。

分步光束传播方法包括：

两步传播方法：分两个步骤估算菲涅尔衍射积分，网格间隔可以通过两个传播的距离进行调整；

角频谱传播方法：使用了菲涅尔衍射积分卷积形式的一些代数运算，运算引入了一个直接设定观察面网格间隔的自由参数。

二 大气湍流

给出大气湍流的基础理论

首先，介绍了Kolmogorov对湍流的初始分析，这一理论最终产生了大气湍流折射率起伏空间功率谱模型。

然后，利用微扰理论（Rytov和Born近似方法）求解由麦克斯韦方程组的得到的波动方程，从而得到观察面光场有用的统计属性。

注：事实证明，Born近似和Rytov近似方法仅在弱湍流起伏区域或短距离传输时有效，两者的主要区别在于Born近似方法认为湍流扰动项是加性的，而Rytov近似方法认为湍流扰动性是乘性的，适用于弱到强湍流起伏区域的是广义Huygens-Fresnel衍射积分方法。

大气性质（如log振幅、相位和辐照度等）的方差、相位和光谱密度发挥两个与模拟相关的工作：

第一个作用：产生分步光束传播方法相互作用因子的随机图像；

第二个作用：在仿真湍流介质传播之后，处理观察平面场来确定大气统计性质，并与理论结果进行比较，证明仿真结果的正确性。

分层大气模型

若大气湍流是一个简单的统计模型，则有可能推导出大气湍流影响光束传播的解析结果。

然而，当需要考虑更复杂的场景时（如使用自适应光学系统），通常不能求解出修正光场统计量的收敛解。

为了数学上的简化，一种常用的技术就是将湍流处理成有限数目的分立层。这个方法常用于实验室内的解析计算、计算机模拟和湍流仿真。

每一层作为一个单位振幅的薄相位屏，表征一个非常厚的湍流体积。如果相位屏后面的厚度远远小于屏后的传播距离，则认为相位屏是薄的。

相位屏是大气相位扰动的一种实现方法，且其联合式（9.2）可计算出折射率算符的表达式，这就是如何将大气相位屏引入分步光束传播方法来仿真大气传播的方法。

1. 分层湍流理论

为从理论上将大气表征为相位屏，可以简单地把湍流曲线改写成有效结构参数项Cni^2（局部湍流强度的度量），沿传播路径位置zi和第i个相位屏对应扩展湍流平板的厚度Δzi的形式

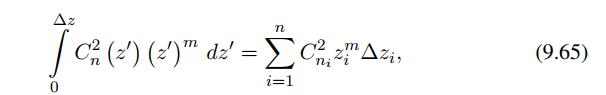
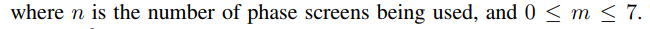
基于上述改写，利用有效结构参数项Cni^2计算的大气相干直径r0与平面波pw或发散球面波sw（点）源，log振幅方差δ_Χ²积分形式可以写成离散形式

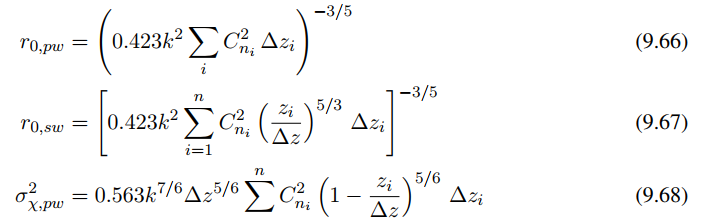
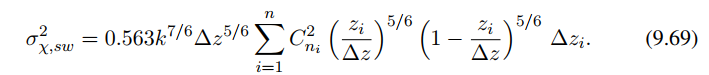
进而表示成第i层相干半径的关系式

举例说明

2.蒙特卡洛相位屏

   见下一节