zkw线段树学习笔记

今天模拟赛线段树被卡常了，由于我自带常数 $buff$，所以学了下zkw线段树。

平常的线段树无论是修改还是查询，都是从根开始递归找到区间的，而zkw线段树直接从叶子结点开始操作。

建树

首先，我们需要把线段树补成一个堆形态的树，原序列在最后一层(最后一层的左右要留空，后面再讲为什么)，这样一来，就可以轻松得出：原序列里第 $x$ 个元素在线段树里的编号就是 $x+2^k$ (其中 $k$ 为线段树的深度，根节点深度为 $0$ )

大概就是这样：

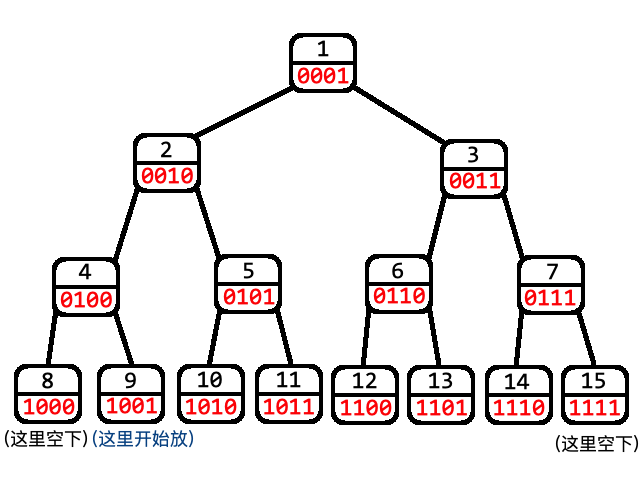
不难发现最后一层节点掐头去尾，就是原序列编号加上二进制最高位上的 $1$。

代码实现也非常简单：

segment_tree(const int n = 0) {

    for (M = 1; M - 2 < n; M <<= 1); //M是最后一层的节点个数

    for (int i = 1; i <= n; ++i)

        t[i + M] = in();

    for (int i = M - 1; i; --i)

        t[i] = t[i << 1] + t[i << 1 | 1]; //合并子树信息

}

单点查询

直接查

单点修改

。。直接上代码：

void update(int p) {

    for (p += M; p; p >>= 1) t[p] += k;

}

区间操作

若当前操作区间为 $[x,y]$，可以把它先转为开区间 $(x-1,y+1)$ (最后一层左右要留空的原因)，设此开区间左右端点在线段树的编号为 $l,r$。

$l, r$ 同时向它们的父亲节点跳，若 $l$ 是它父亲的左儿子，则它父亲的右儿子被操作( $r$ 与 $l$ 对称)，直到 $l,r$ 的父亲相同。

可以配合图片理解：

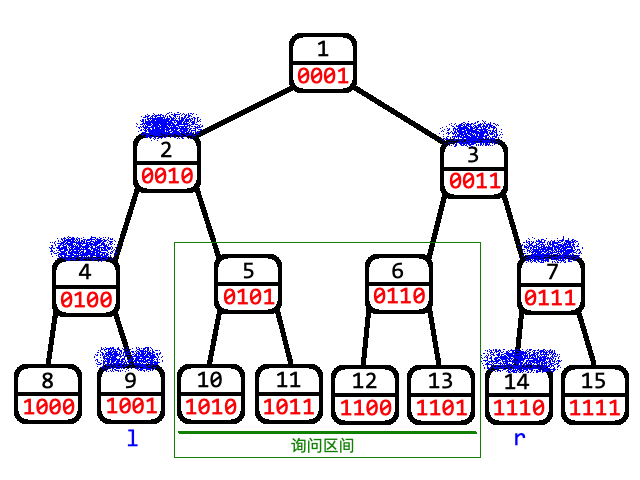
上图中：蓝色为 $l,r$ 会跳到的点。因为查询区间为 $l$ 右边和 $r$ 左边组成的区间，当 $l$ 为父亲的左儿子时，它父亲的右儿子一定在它左边( $r$ 与 $l$ 对称)。

区间修改、查询

这里以区间加法为例；

在普通的线段树中，一般用 $lazy$ $tag$ 来解决这个问题，zkw线段树同样可以，但从上向下操作、下放 $lazy$ $tag$ 等操作并不优雅 常数大。

可以采用标记永久化，随用随查，按zkw的说法——永久化的标记就是值。

考虑上文提到的区间操作的过程，自下向上走的过程中，根据遇到的标记来计算贡献。

具体实现细节可以看代码：

void modify(int l, int r, ll k) {

    int lnum = 0, rnum = 0, now = 1;

    //lnum 表示当前左端点走到的子树有多少个元素在修改区间内 (rnum与lnum对称)

    //now 表示当前端点走到的这一层有多少个叶子节点

    for (l = l + M - 1, r = r + M + 1; l ^ r ^ 1; l >>= 1, r >>= 1; now <<= 1) {

        t[l] += k * lnum, t[r] += k * rnum;

        if (~l & 1) t[l ^ 1] += k * now, add[l ^ 1] += k, lnum += now;

        if (r & 1)  t[r ^ 1] += k * now, add[r ^ 1] += k, rnum += now;

    }

    for (; l; l >>= 1, r >>= 1)

        t[l] += k * lnum, t[r] += k * rnum;

}

long long query(int l, int r) {

    int lnum = 0, rnum = 0, now = 1;

    long long ret = 0;

    for (l = l + M - 1, r = r + M + 1; l ^ r ^ 1; l >>= 1, r >>= 1, now <<= 1) {

        if (add[l]) ret += add[l] * lnum;

        if (add[r]) ret += add[r] * rnum;

        if (~l & 1) ret += t[l ^ 1], lnum += now;

        if (r & 1)  ret += t[r ^ 1], rnum += now;

    }

    for (; l; l >>= 1, r >>= 1)

        ret += add[l] * lnum, ret += add[r] * rnum;

    return ret;

}

参考文献：《统计的力量》—— zkw