轮廓线DP
轮廓线DP
刚刚学了轮廓线DP,想了好久才懂。
我的理解就是用一条线的状态去更新另一条线的状态,然后将格子填满。
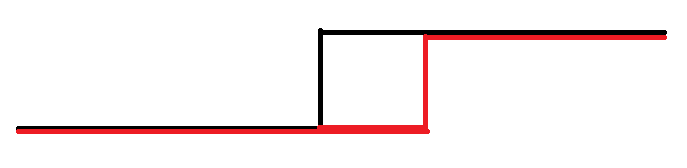
图中正方形即是要填东西(根据题意)的格子,红线的状态是由黑线转移过来的。
对于每一条线都有一个自己的状态(一个二进制数,先不用看1和0是啥意思),如下图。
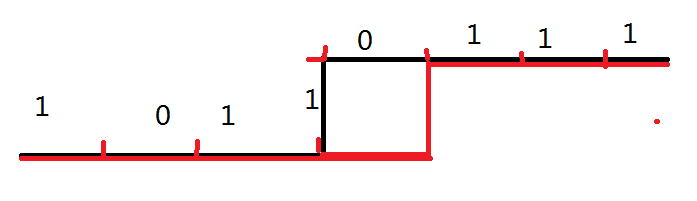
图中黑线的状态即是11101101(最左边的是二进制位第零位),编号从左往右为1,2,3,4,5,6,7,8。
具体一点,我们上例题。
题目大意:给你一个\(n*m\)\((1 <= n,m <= 100)\)的网格,让你在网格里填上长度不小于2的线段,问有多少种情况,对结果%\(1e9 + 7\)。
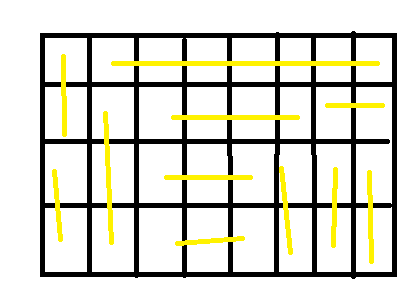
这是某一种情况。
现在我们轮廓线上的1和0就有意义了:如果竖着的这条线上的数为1的话,那么这个格子必须画一条横线(图一);如果横着的这条线上的数为1的话,那么这个格子必须画一条竖线(图二);我们发现,横线和竖线上不能同时为1,这是冲突的;如果横线和竖线上都为0,那么这个格子里话横线竖线都可以。
(不会画图,丑死了)
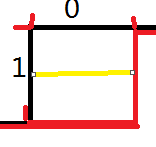 (图一)
(图一)
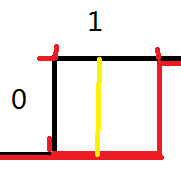 (图二)
(图二)
下面为了好打,把图一定义为(1, 0),图二定义为(0,1)。\(a[]\)是二进制数,\(i\)是下标:(\(a[i - 1]\), \(a[i]\))
对于一个格子,它上面的黑线有三种情况:(1, 0),(0, 1),(0, 0)。然后我们考虑怎么将黑线的状态转移到红线。
<1> 当黑线为(1,0)时,红线可以转移到的状态有:(0,1),(0,0)。(其他位上二进制数都一样)
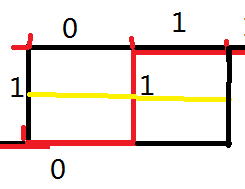

<2> 当黑线为(0,1)时,红线可以转移到的状态有:(1,0),(0,0)。
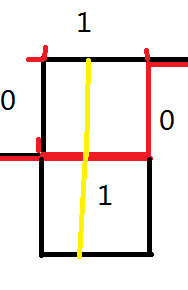
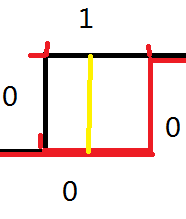
<3> 当黑线为(0,0)时,红线可以转移到的状态有:(0,1),(1,0)。(差不多,就不画了)
像这样一直转移下去,填完\(n*m\)个格子,就可以得到所有的方案。
我们考虑开一个二维\(unordered\) _ \(map\),\(unordered\)_\(map<int , long long> dp[2]\);\(dp[0,1][x] = val\),第一维是个滚动数组,第二维\(x\)是这条轮廓线的状态,\(val\)是这条线填完对应的那个格子后合法的方案数。
为啥用\(unordered\)\(map\),而不用\(map\)呢?\(map\): 该类型的搜索时间复杂度为\(O(logn)\) ;\(unordered_map\) : 搜索时间复杂度\(O(1)\)为平均时间,最坏情况下的时间复杂度为\(O(n)\);
#include <iostream>
#include <cstdio>
#include <unordered_map>
using namespace std;
const int p = 1e9 + 7;
int n, m;
void work(int n, int m) {
unordered_map <int, long long> dp[2];
int now = 0, nxt = 1;
dp[now][0] = 1;
for(int i = 1;i <= n; i++) {
for(int j = 1;j <= m; j++) {
dp[nxt].clear();
for(auto k = dp[now].begin();k != dp[now].end(); k++) {
int nowst = k -> first, nowval = k -> second;
int u = (nowst >> j) & 1, l = (nowst >> (j - 1)) & 1;
if(u == 0 && l == 0) {
(dp[nxt][nowst ^ (1 << j)] += nowval) %= p;
(dp[nxt][nowst ^ (1 << (j - 1))] += nowval) %= p;
}
else if(u == 1 && l == 0) {
(dp[nxt][nowst ^ (1 << j)] += nowval) %= p;
(dp[nxt][nowst ^ (1 << j) ^ (1 << (j - 1))] += nowval) %= p;
}
else if(u == 0 && l == 1) {
(dp[nxt][nowst ^ (1 << (j - 1))] += nowval) %= p;
(dp[nxt][nowst ^ (1 << j) ^ (1 << (j - 1))] += nowval) %= p;
}
}
swap(now, nxt);
}
dp[nxt].clear();
for(auto k = dp[now].begin();k != dp[now].end(); k++) {
int nowst = k -> first, nowval = k -> second;
if((nowst >> m) ^ 1) dp[nxt][nowst << 1] = nowval;
}
swap(now, nxt);
}
printf("%d", dp[now][0]);
}
int main() {
scanf("%d %d", &n, &m);
work(n, m);
return 0;
}
我也是刚学,哪说的不对的还希望大佬指出。
轮廓线DP的更多相关文章
- 轮廓线DP POJ3254 && BZOJ 1087
补了一发轮廓线DP,发现完全没有必要从右往左设置状态,自然一点: 5 6 7 8 9 1 2 3 4 如此设置轮廓线标号,转移的时候直接把当前j位改成0或者1就行了.注意多记录些信息对简化代码是很有帮 ...
- HDU4804 Campus Design 轮廓线dp
跟上面那篇轮廓线dp是一样的,但是多了两个条件,一个是在原图上可能有些点是不能放的(即障碍),所以转移的时候要多一个判断color[i][j]是不是等于1什么的,另外一个是我们可以有多的1*1的骨牌, ...
- POJ2411 Mondriaan's Dream 轮廓线dp
第一道轮廓线dp,因为不会轮廓线dp我们在南京区域赛的时候没有拿到银,可见知识点的欠缺是我薄弱的环节. 题目就是要你用1*2的多米诺骨排填充一个大小n*m(n,m<=11)的棋盘,问填满它有多少 ...
- UVA - 11270 轮廓线DP
其实这题还能用状压DP解决,可是时间达到2000ms只能过掉POJ2411.状压DP解法详见状压DP解POJ2411 贴上POJ2411AC代码 : 2000ms 时间复杂度h*w*(2^w)*(2^ ...
- [UOJ422][集训队作业2018]小Z的礼物——轮廓线DP+min-max容斥
题目链接: [集训队作业2018]小Z的礼物 题目要求的就是最后一个喜欢的物品的期望得到时间. 根据$min-max$容斥可以知道$E(max(S))=\sum\limits_{T\subseteq ...
- 【UOJ#422】【集训队作业2018】小Z的礼物(min-max容斥,轮廓线dp)
[UOJ#422][集训队作业2018]小Z的礼物(min-max容斥,轮廓线dp) 题面 UOJ 题解 毒瘤xzy,怎么能搬这种题当做WC模拟题QwQ 一开始开错题了,根本就不会做. 后来发现是每次 ...
- BZOJ.4572.[SCOI2016]围棋(轮廓线DP)
BZOJ 洛谷 \(Description\) 给定\(n,m,c\).\(Q\)次询问,每次询问给定\(2*c\)的模板串,求它在多少个\(n*m\)的棋盘中出现过.棋盘的每个格子有三种状态. \( ...
- 4572: [Scoi2016]围棋 轮廓线DP KMP
国际惯例的题面:这种题目显然DP了,看到M这么小显然要状压.然后就是具体怎么DP的问题.首先我们可以暴力状压上一行状态,然后逐行转移.复杂度n*3^m+3^(m*2),显然过不去. 考虑状态的特殊性, ...
- Solid Dominoes Tilings (轮廓线dp打表 + 容器)
第一步先打一个表,就是利用轮廓线DP去打一个没有管有没有分界线组合数量的表 #include<bits/stdc++.h> using namespace std; ; <<; ...
- HDU 4802 && HDU 4803 贪心,高精 && HDU 4804 轮廓线dp && HDU 4805 计算几何 && HDU 4811 (13南京区域赛现场赛 题目重演A,B,C,D,J)
A.GPA(HDU4802): 给你一些字符串对应的权重,求加权平均,如果是N,P不计入统计 GPA Time Limit: 2000/1000 MS (Java/Others) Memory ...
随机推荐
- Mac IDEA 免激活破解版 亲测有效 2020.8.1记
开局一张图 下载地址 链接: https://pan.baidu.com/s/1OKbYCRQiZ3ip0Gzle5wydg 密码: iwfb 步骤 卸载之前的IDEA(没安装过,可忽略) 将下载后的 ...
- day23:单继承&多继承&菱形继承&__init__魔术方法
1.单继承 1.1 关于继承的一些基本概念 1.2 子类可以调用父类的公有成员 1.3 子类无法调用父类的私有成员 1.4 子类可以改写父类的方法 2.多继承 2.1 多继承的基本语法 2.2 sup ...
- 嵌入式linux简介
嵌入式linux系统应用非常广泛,涵盖各行各业,基于ARM.mips等微处理器架构的硬件平台.基于嵌入式linux系统的设备已经深入生活中各个角落,随处可见. 我们常说的嵌入式linux系统,其实 ...
- Python-关于正则表达式的总结
什么是正则表达式? 正则表达式(regular expression)描述了一种字符串匹配的模式(pattern),用于字符串的 匹配 和 提取 等操作.正则表达式在所有编程语言中都是通用的. 很多人 ...
- CentOS7安装Redis的两种方式
1. 源码安装方式(不推荐): https://www.cnblogs.com/zuidongfeng/p/8032505.html https://www.cnblogs.com/zerotomax ...
- html笔记 标签属性、图像和链接、超链接
HTML 标签属性: <b></b>:加粗 <i></i>:斜体 <u></u>:下划线 <s></s> ...
- JS的赋值与深浅拷贝实例
赋值 基本类型: 传值,在栈内存中的数据发生数据变化的时候,系统会自动为新的变量分配一个新的之值在栈内存中,两个变量相互独立,互不影响的 引用类型: 传址,只改变指针的指向,指向同一个对象,两个变量相 ...
- Name jms can't bind to context问题解决
需要把gis-datamanage包中的配置test改成compile
- 【CF1110E】 Magic Stones - 差分
题面 Grigory has n n magic stones, conveniently numbered from \(1\) to \(n\). The charge of the \(i\)- ...
- 运用sklearn进行线性判别分析(LDA)代码实现
基于sklearn的线性判别分析(LDA)代码实现 一.前言及回顾 本文记录使用sklearn库实现有监督的数据降维技术——线性判别分析(LDA).在上一篇LDA线性判别分析原理及python应用(葡 ...
