Seq2Seq原理详解

一、Seq2Seq简介

　　seq2seq 是一个Encoder–Decoder 结构的网络，它的输入是一个序列，输出也是一个序列。Encoder 中将一个可变长度的信号序列变为固定长度的向量表达，Decoder 将这个固定长度的向量变成可变长度的目标的信号序列。
　　很多自然语言处理任务，比如聊天机器人，机器翻译，自动文摘，智能问答等，传统的解决方案都是检索式(从候选集中选出答案)，这对素材的完善程度要求很高。seq2seq模型突破了传统的固定大小输入问题框架。采用序列到序列的模型，在NLP中是文本到文本的映射。其在各主流语言之间的相互翻译以及语音助手中人机短问快答的应用中有着非常好的表现。

二、编码解码模型

　　1、模型框架

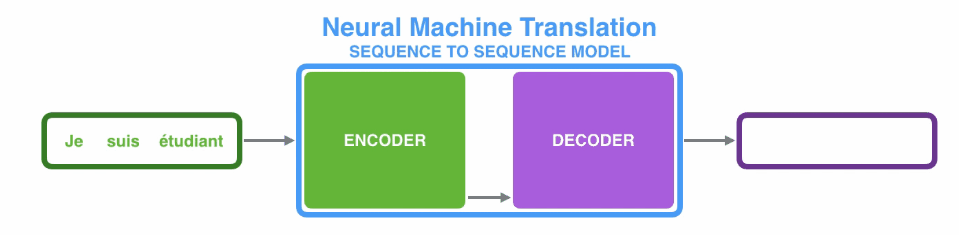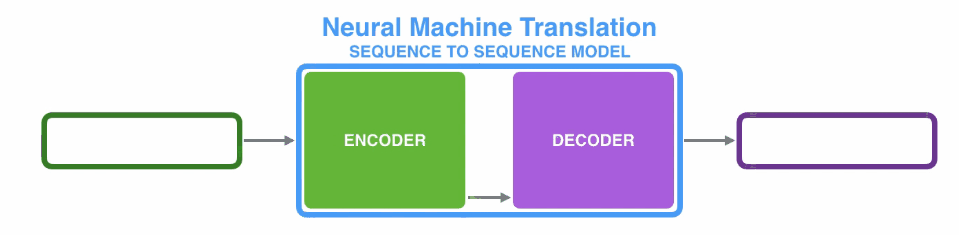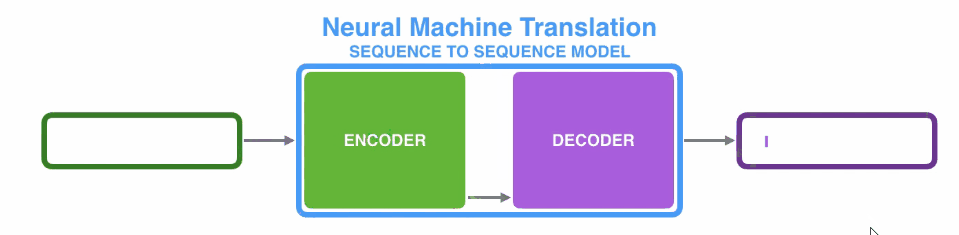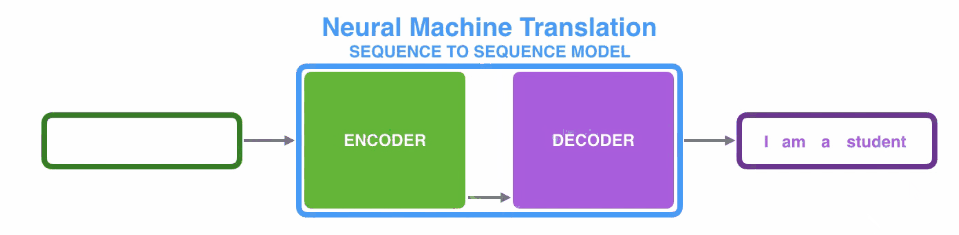
　　在NLP任务中，其实输入的是文本序列，输出的很多时候也是文本序列，下图所示的是一个典型的机器翻译任务中，输入的文本序列(源语言表述)到输出的文本序列(目标语言表述)之间的变换。

　　2、编码解码器结构

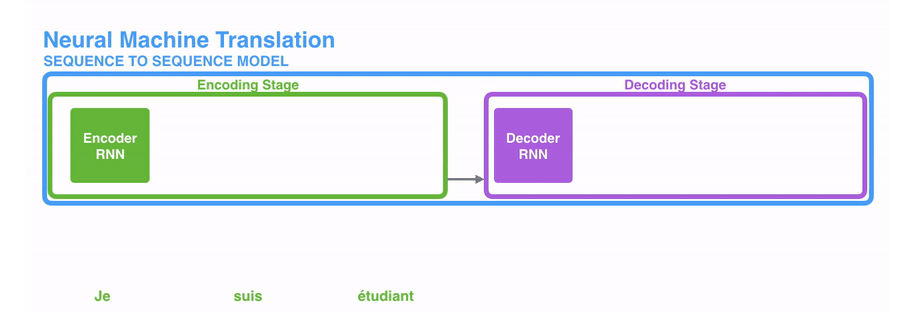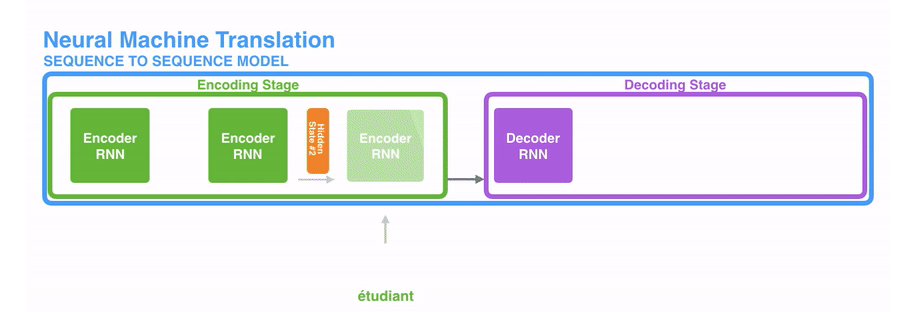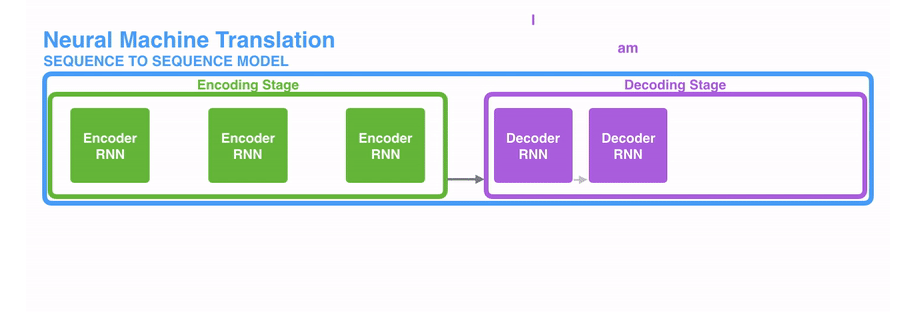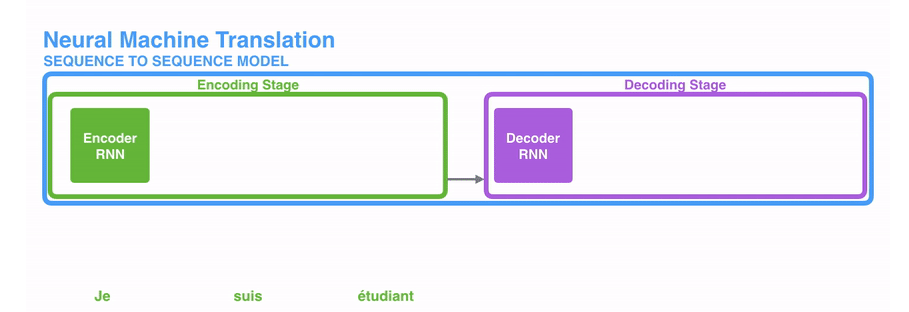
　　（1）编码器处理输入序列中的每个元素(在这里可能是1个词)，将捕获的信息编译成向量（称为上下文内容向量）。在处理整个输入序列之后，编码器将上下文发送到解码器，解码器逐项开始产生输出序列。如，机器翻译任务

　　（2）上下文向量

• 输入的数据(文本序列)中的每个元素(词)通常会被编码成一个稠密的向量，这个过程叫做word embedding
• 经过循环神经网络（RNN），将最后一层的隐层输出作为上下文向量
• encoder和decoder都会借助于循环神经网络(RNN)这类特殊的神经网络完成，循环神经网络会接受每个位置(时间点)上的输入，同时经过处理进行信息融合，并可能会在某些位置(时间点)上输出。如下图所示。
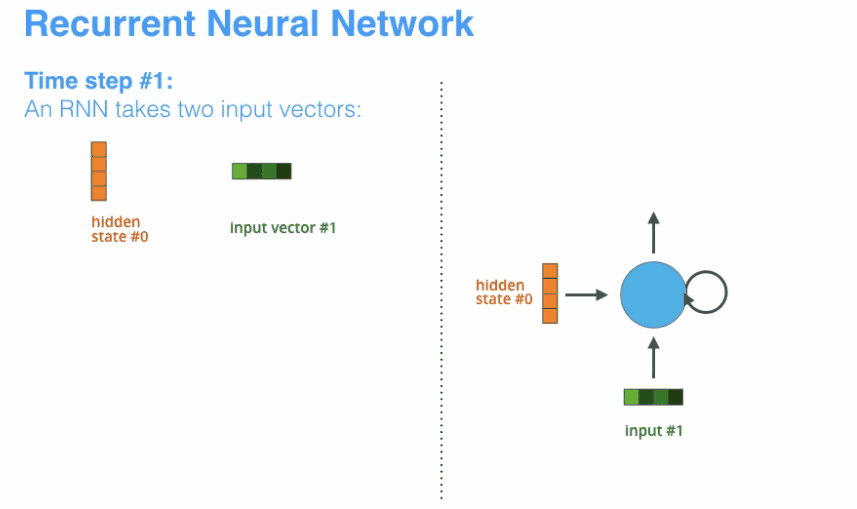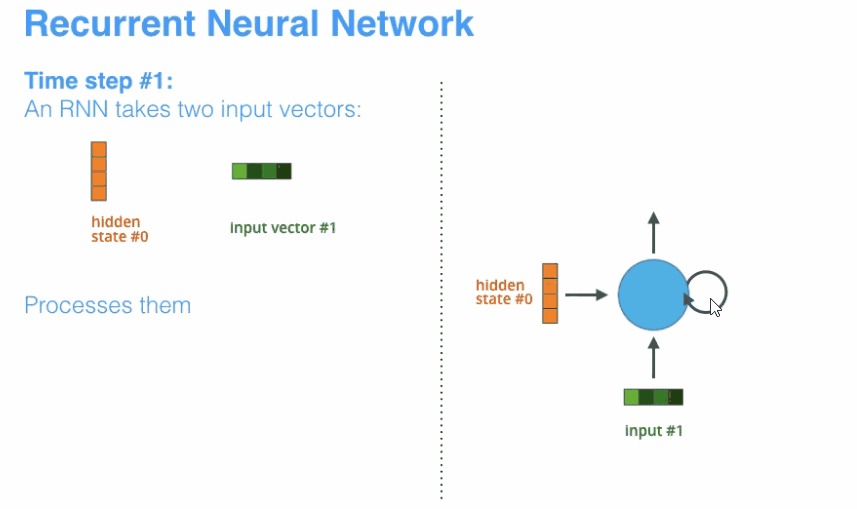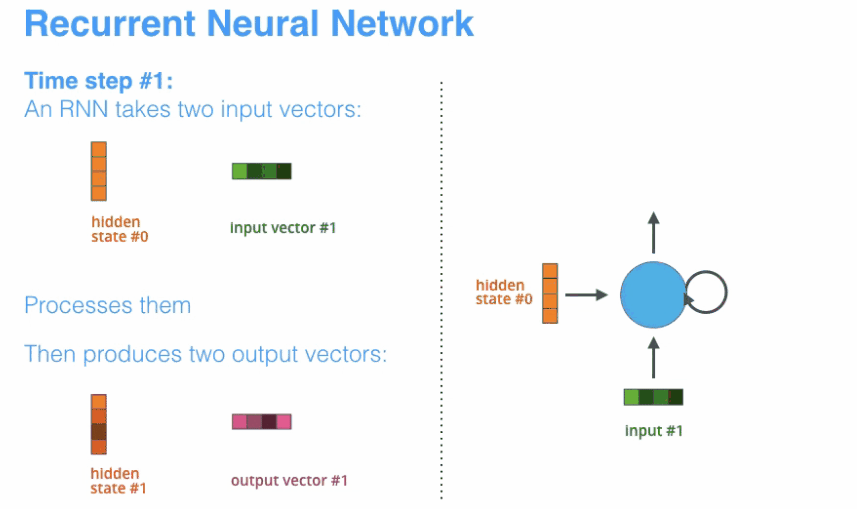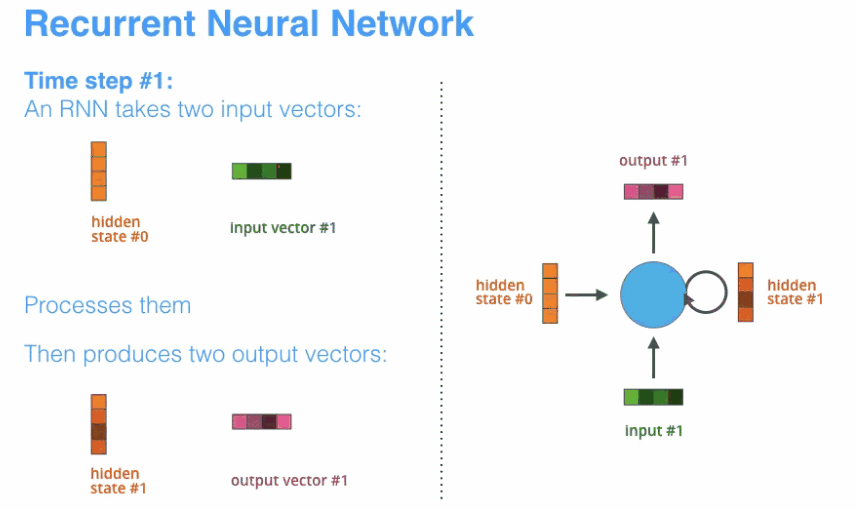
  动态地展示整个编码器和解码器，分拆的步骤过程：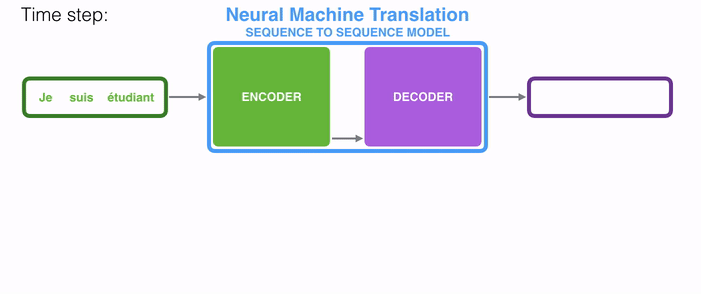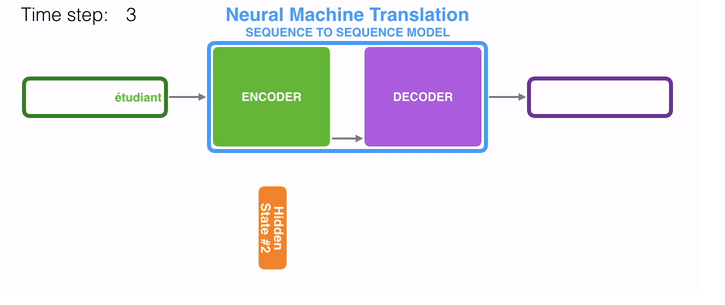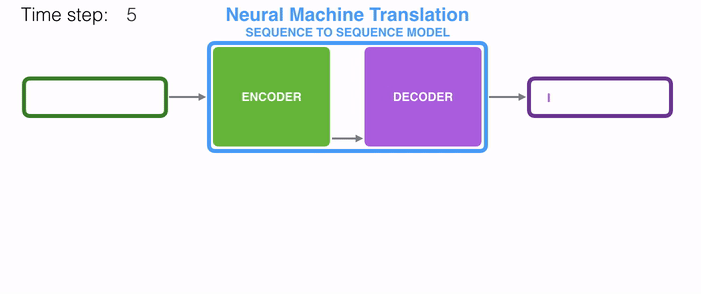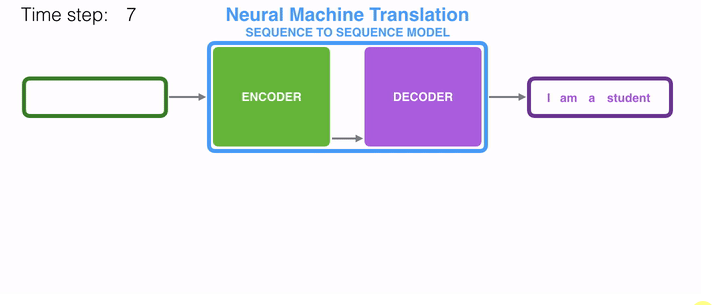
  更详细地展开，其实是这样的：
  

三、加入attention注意力机制的Seq2Seq

　　1、为什么加入attention机制：

　　提升效果，不会寄希望于把所有的内容都放到一个上下文向量(context vector)中，而是会采用一个叫做注意力模型的模型来动态处理和解码，动态的图如下所示。

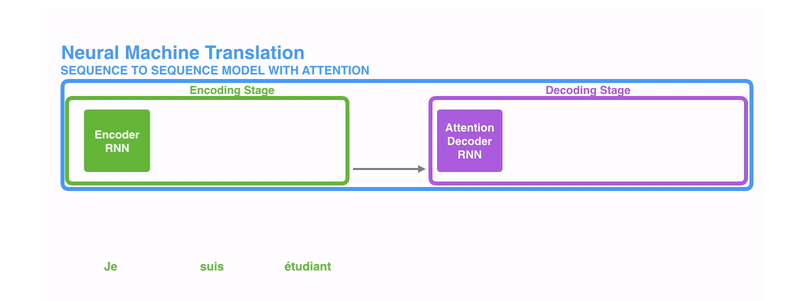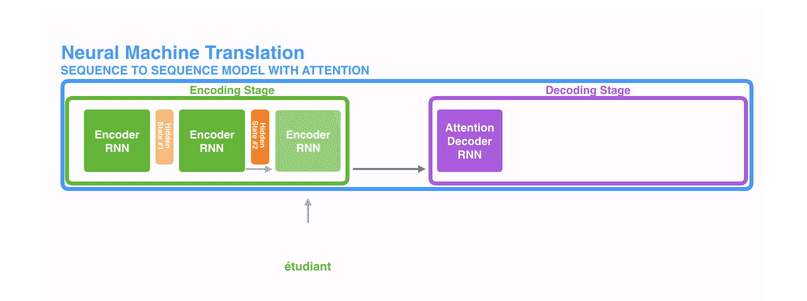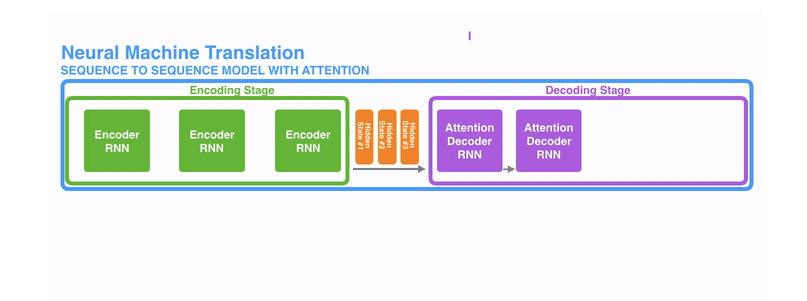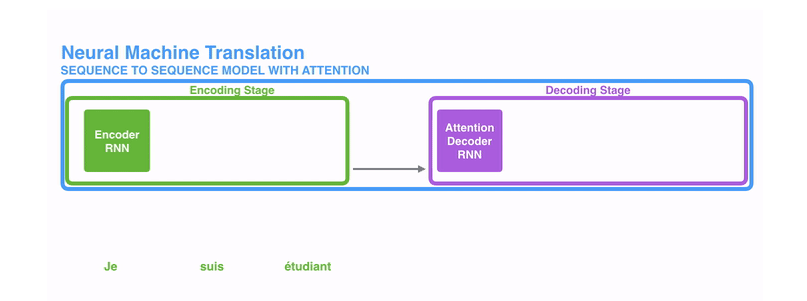
　　所谓的注意力机制，可以粗略地理解为是一种对于输入的信息，根据重要程度进行不同权重的加权处理(通常加权的权重来源于softmax后的结果)的机制，如下图所示，是一个在解码阶段，简单地对编码器中的hidden states进行不同权重的加权处理的过程。

　　2、attention机制结构

　　3、加入attention机制的Seq2Seq原理

• 带注意力的解码器RNN接收的嵌入(embedding)和一个初始的解码器隐藏状态(hidden state)。
• RNN处理输入，产生输出和新的隐藏状态向量（h4），输出被摒弃不用。
• attention的步骤：使用编码器隐藏状态(hidden state)和h4向量来计算该时间步长的上下文向量（C4）。
• 把h4和C4拼接成一个向量。
• 把拼接后的向量连接全连接层和softmax完成解码
• 每个时间点上重复这个操作
  

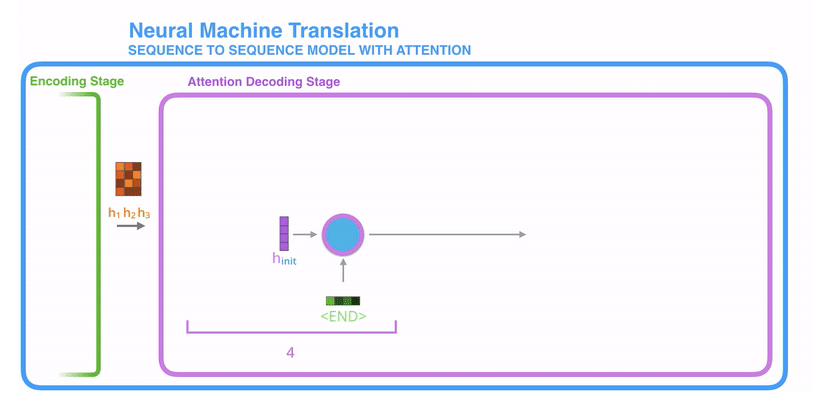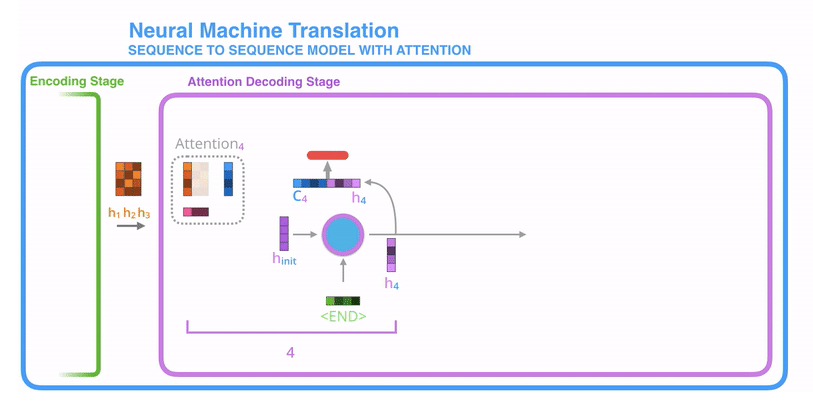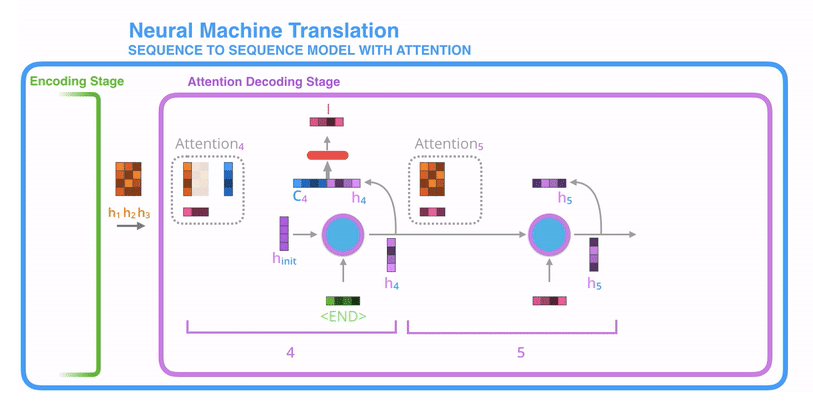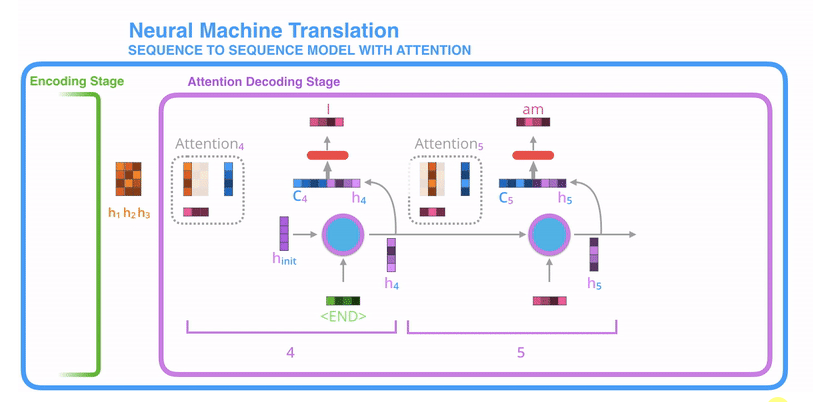
　　也可以把这个动态解码的过程展示成下述图所示的过程。

四、图解Attention Seq2Seq

输入：$x = (x_1,...,x_{T_x})$

输出：$y = (y_1,...,y_{T_y})$

1、$h_t = RNN_{enc}(x_t, h_{t-1})$，Encoder方面接受的每一个单词word embedding，和上一个时间点的hidden state。输出的是这个时间点的hidden state。

2、$s_t = RNN_{dec}(\hat{y_{t-1}},s_{t-1})$，Decoder方面接受的是目标句子里单词的word embedding，和上一个时间点的hidden state。

3、$c_i = \sum_{j=1}^{T_x} \alpha_{ij}h_j$，context vector是一个对于encoder输出的hidden states的一个加权平均。

4、$\alpha_{ij} = \frac{exp(e_{ij})}{\sum_{k=1}^{T_x}exp(e_{ik})}$，每一个encoder的hidden states对应的权重。

5、$e_{ij} = score(s_i, h_j)$，通过decoder的hidden states加上encoder的hidden states来计算一个分数，用于计算权重(4)

6、$\hat{s_t} = tanh(W_c[c_t;s_t])$，将context vector 和 decoder的hidden states 串起来。

7、$p(y_t|y_{<t},x) = softmax(W_s\hat{s_t})$，计算最后的输出概率。

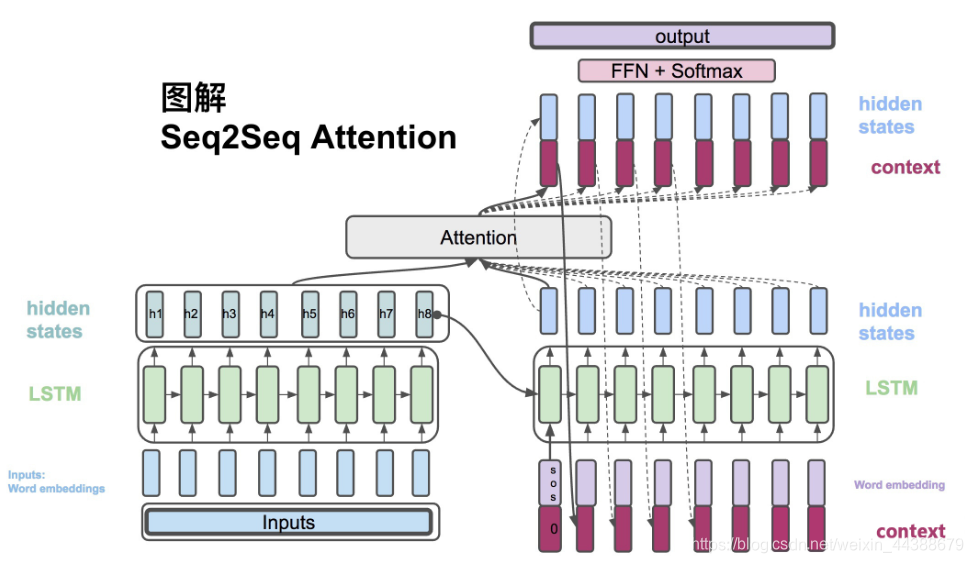
(1)$h_t = RNN_{enc}(x_t, h_{t-1})$，Encoder方面接受的是每一个单词word embedding，和上一个时间点的hidden state。输出的是这个时间点的hidden state。

(2)$s_t = RNN_{dec}(\hat{y_{t-1}},s_{t-1})$，Decoder方面接受的是目标句子里单词的word embedding，和上一个时间点的hidden state。

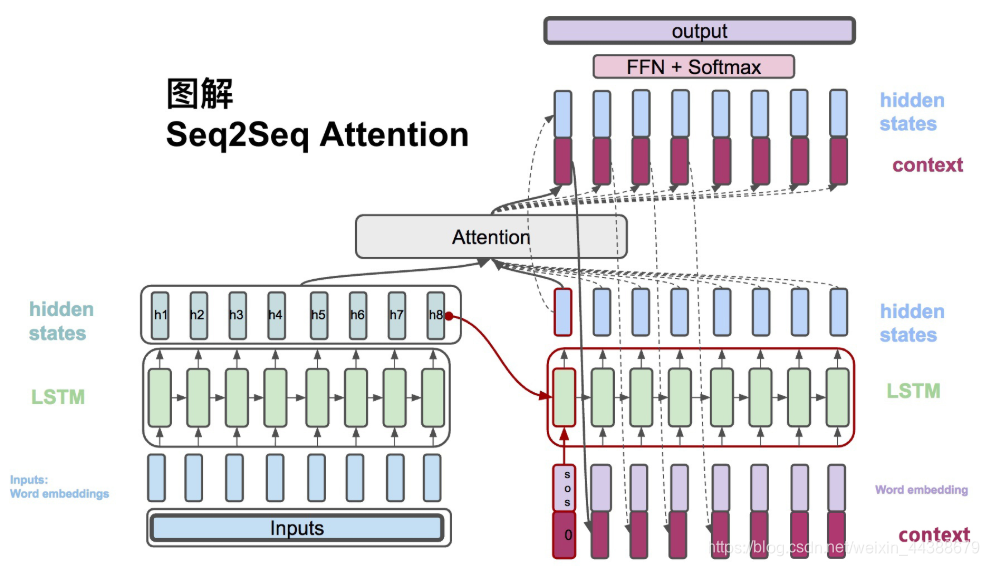
(3)、$c_i = \sum_{j=1}^{T_x} \alpha_{ij}h_j$，context vector是一个对于encoder输出的hidden states的一个加权平均。

(4)、$\alpha_{ij} = \frac{exp(e_{ij})}{\sum_{k=1}^{T_x}exp(e_{ik})}$，每一个encoder的hidden states对应的权重。

(5)、$e_{ij} = score(s_i, h_j)$，通过decoder的hidden states加上encoder的hidden states来计算一个分数，用于计算权重(4)

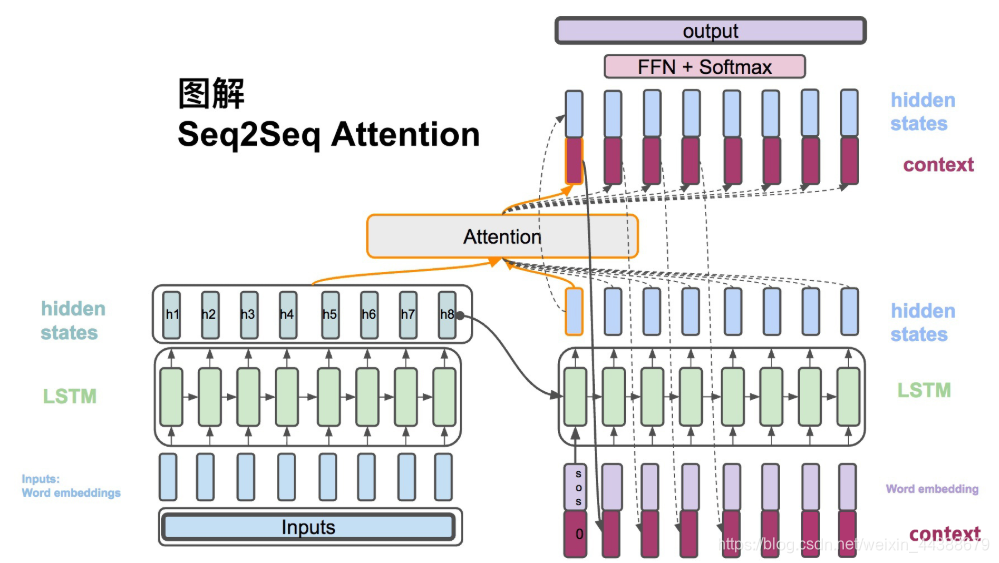
下一个时间点：

(6)$\hat{s_t} = tanh(W_c[c_t;s_t])$，将context vector 和 decoder的hidden states 串起来。

(7)$p(y_t|y_{<t},x) = softmax(W_s\hat{s_t})$，计算最后的输出概率。

五、三种Attention得分计算方式

　　在luong中提到了三种score的计算方法。这里图解前两种：

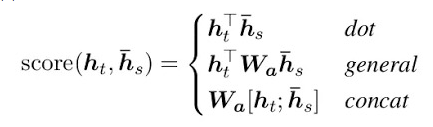
　　1、方法一

　　输入是encoder的所有hidden states H: 大小为(hid dim, sequence length)。decoder在一个时间点上的hidden state， s： 大小为（hid dim, 1）。
　　（1）旋转H为（sequence length, hid dim) 与s做点乘得到一个 大小为(sequence length, 1)的分数。
　　（2）对分数做softmax得到一个合为1的权重。
　　（3）将H与第二步得到的权重做点乘得到一个大小为(hid dim, 1)的context vector。

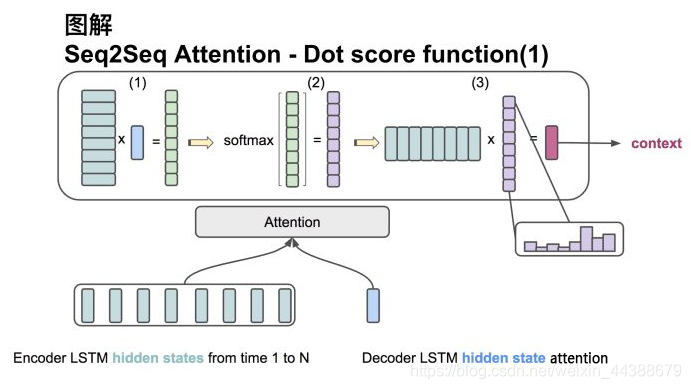
　　2、方法二

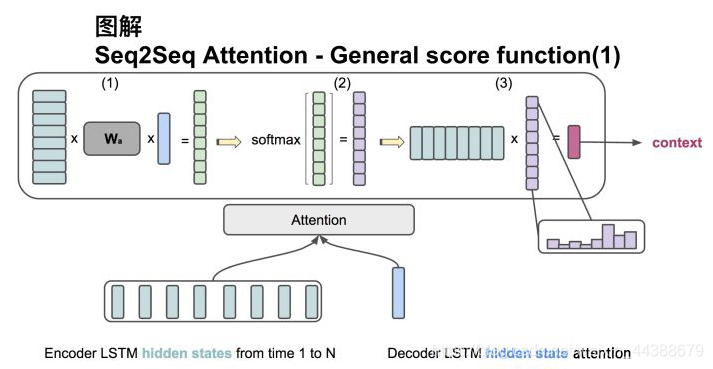
　　输入是encoder的所有hidden states H: 大小为(hid dim1, sequence length)。decoder在一个时间点上的hidden state， s： 大小为（hid dim2, 1）。此处两个hidden state的纬度并不一样。
　　（1）旋转H为（sequence length, hid dim1) 与 Wa [大小为 hid dim1, hid dim 2)] 做点乘， 再和s做点乘得到一个 大小为(sequence length, 1)的分数。
　　（2）对分数做softmax得到一个合为1的权重。
　　（3）将H与第二步得到的权重做点乘得到一个大小为(hid dim, 1)的context vector。

 

本文转载自：https://blog.csdn.net/weixin_44388679/article/details/102575223

附：版权声明：本文为博主(马苏比拉米G )原创文章，遵循CC 4.0 BY-SA版权协议

 

 

.MathJax, .MathJax_Message, .MathJax_Preview { display: none }