[ZJOI2007]仓库建设（斜率dp优化）

前言

---

纪念一下我做的第二道斜率优化$dp$题，终于自己能把代码敲出来了，然而有很智障的$bug$，把$i$写成$q[i]$，找了半天QAQ。然后写$dp$公式并优化的能力稍微强了一点(自我感觉良好)，对于斜率优化$dp$"去尾"的操作理解更深刻了

描述

---

$1∼N$号工厂，第$i$个工厂有$P_{i}$个成品，第$i$个工厂建立仓库需要$C_{i}$的费用，该工厂距离第一个工厂的距离为$X_{i}$，编号小的工厂只能往编号大的工厂搬用成品，每单位成品搬每单位距离需要花费1，问所有成品搬到工厂里面所需的最少费用是多少　[Link]

分析

---

设$f[i]$为第$i$个工厂建立仓库，前$i$个工厂的成品都搬到仓库中的最小花费，则容易得到动态转移方程:

　　　　　　　　　$f[i]=min(f[j]+P_{j+1}(X_{i}-X_{j+1})+P_{j+2}(X_{i}-X_{j+2})+\cdots +P_{i-1}(X_{i}-X_{i+1}))+Ci$

通式为

　　　　　　　　　　　　　　　$f[i]=min(f[j]+\sum_{k=j+1}^{i-1}P_{k}\cdot X_{i}-\sum_{k=j+1}^{i-1}P_{k}\cdot X_{k})+C_{i}$

令 $s[i]=\sum_{1}^{i}P[i],g[i]=\sum_{1}^{i}P_{i}\cdot X_{i}$
则方程变为
　　　　　　　　　　　　　　　$f[i]=min(f[j]+X_{i}\cdot(s[i−1]−s[j])-(g[i−1]−g[j]))+C_{i}$

则对于最优决策 $j$ ，有

　　　　　　　　　　　　　　　　　$f[j]+g[j]=X_{i}\cdot s[j]+f[i]-X_{i}\cdot s[i−1]−Ci$

也就是要找 $y=kx+b$，$k$已知，找一对$x,y$使得截距最小

Code

#include <cstdio>
#define ll long long
#define empty (head>=tail)
const int maxn = 1e6+10;
ll n, head, tail, j;
ll x[maxn], p[maxn], c[maxn];
ll q[maxn], s[maxn], g[maxn], f[maxn];
inline long double X(ll i) {return s[i];}
inline long double Y(ll i) {return f[i]+g[i];}
inline long double rate(ll j,ll k) {return (Y(k)-Y(j))/(X(k)-X(j));}
int main()
{
    scanf("%lld", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%lld%lld%lld", &x[i], &p[i], &c[i]);
        s[i] = s[i-1]+p[i], g[i] = g[i-1]+p[i]*x[i];
    }
    head = tail = 1;
    for(int i = 1; i <= n; i++){
        while(!empty&&rate(q[head],q[head+1])<x[i])head++;
        j = q[head]; f[i] = f[j]+x[i]*(s[i-1]-s[j])-(g[i-1]-g[j])+c[i];
        while(!empty&&rate(q[tail-1],q[tail])>rate(q[tail],i))tail--;
        q[++tail] = i;
    }
    printf("%lld\n", f[n]);
} 

思考

---

之前入门的题目说过，假如$g(c,b)<=g(b,a)$，那么这个$b$就没有任何用武之地了，就把这样的点去掉后再加入新的点。那么我会想到，能不能先不去掉这个$b$，直接加入新的点，就是在斜率小于$A[i]$的时候再去掉不也可以么，顶多时间长一点，然而现实给了我一发$WA$。我就去想为什么会是这个亚子？原因在于，必须保证通过前面的状态得到的$f[i]$为最优，而你的$b$可能会导致你通过原有的方式得到的$f[i]$并不是最优的，那么得到的$f[n]$自然不一定是最优解。

那我就去做了尝试，我的确没有去掉$b$，那么我只要从之前的状态里挑最优不也可以么，交上去之后发现的确可以(妥妥$WA$)。这就很头疼，也证明我的想法是不对的，因为在有$b$的前提下，你按照原来那种判断两点间斜率的方法去决定取哪个点的方法并不能确定哪个点是最优的，比如下图：

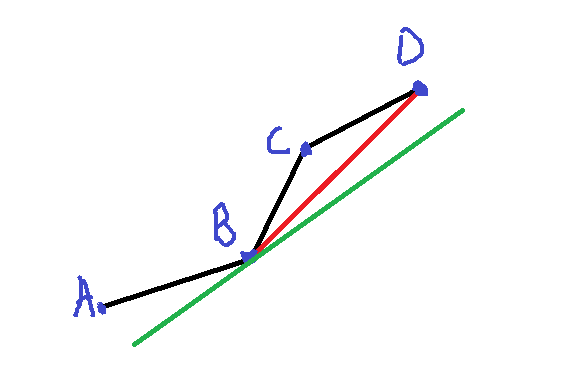
这个时候$C$是不满足要求的点，我没有去掉，之后我从$A,B,C,D$中挑选最优的点去更新$E$点，$E$对应的斜率$rate$是绿色的那条线，从最下面开始扫描，$AB$的斜率小于$rate$，扫到$B$这里停下，由于$BC$斜率大于$rate$，还是在$B$这里，之后$CD$的斜率比$rate$小，那就扫到$D$这里停下，然后通过$D$更新$E$点。但是你会发现其实$B$点比$D$点更优，这样选是不对的。但是如果我先把$C$点去掉，那么通过$AB,BD$的斜率去选择点，你会发现得到的$E$点是最优的

所以结果就是，正是因为满足要求的点之间的斜率是单调递增的才能保证每次得到的$f[i]$为最优，并且这样计算$f[i]$的确效率很高~

附上错误的代码(T_T)：

#include <cstdio>
#define ll long long
#define empty (head>=tail)
const int maxn = 1e6+10;
ll n, head, tail, j;
ll x[maxn], p[maxn], c[maxn];
ll q[maxn], s[maxn], g[maxn], f[maxn];
inline long double X(ll i) {return s[i];}
inline long double Y(ll i) {return f[i]+g[i];}
inline long double rate(ll j,ll k) {return (Y(k)-Y(j))/(X(k)-X(j));}
int main()
{
    scanf("%lld", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%lld%lld%lld", &x[i], &p[i], &c[i]);
        s[i] = s[i-1]+p[i], g[i] = g[i-1]+p[i]*x[i];
    }
    head = tail = 1;
    for (int i = 1; i <= n; i++) {
        int l = head, r = tail;
        while(!empty&&l<r) {
            if(rate(q[l],q[l+1])<x[i]) head = l+1;
            l++;
        }
        j = q[head]; f[i] = f[j]+x[i]*(s[i-1]-s[j])-(g[i-1]-g[j])+c[i];
        q[++tail] = i;
    }
    printf("%lld\n", f[n]);
} 

---

参考文章：

https://www.cnblogs.com/1625--H/p/11267043.html