Python机器学习课程：线性回归算法

本文的文字及图片来源于网络,仅供学习、交流使用,不具有任何商业用途,如有问题请及时联系我们以作处理

最基本的机器学习算法必须是具有单个变量的线性回归算法。如今，可用的高级机器学习算法，库和技术如此之多，以至于线性回归似乎并不重要。但是，学习基础知识总是一个好主意。这样，您将非常清楚地理解这些概念。在本文中，我将逐步解释线性回归算法。

想法和公式

线性回归使用非常基本的预测思想。公式如下：

Y = C + BX

我们在学校都学过这个公式。提醒您，这是一条直线方程。在此，Y是因变量，B是斜率，C是截距。通常，对于线性回归，

它写为：

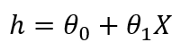
在这里，" h"是假设或预测的因变量，X是输入特征，theta0和theta1是系数。Theta值从头开始随机初始化。然后使用梯度下降，我们将更新theta值以最小化成本函数。这是成本函数和梯度下降的解释。

成本函数和梯度下降

成本函数确定预测与原始因变量的距离。这是公式

任何机器学习算法的想法都是最小化成本函数，以使假设接近于原始因变量。为此，我们需要优化theta值。如果我们分别基于theta0和theta1取成本函数的偏导数，则会得到梯度下降。要更新theta值，我们需要从相应的theta值中减去梯度下降：

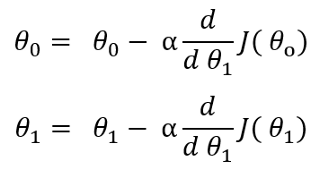
经过偏导数后，以上公式将变为：

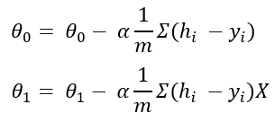
此处，m是训练数据的数量，而alpha是学习率。我正在谈论一种变量线性回归。这就是为什么我只有两个theta值的原因。如果有很多变量，则每个变量都有theta值。

工作实例

我将要使用的数据集来自安德鲁·伍(Andrew Ng)的Coursera机器学习课程。这是在Python中逐步实现线性回归的过程。

(1) 导入包和数据集。

import numpy as np 
import pandas as pd 
df = pd.read_csv('ex1data1.txt', header = None) 
df.head() 

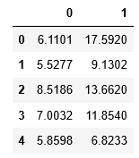
在此数据集中，列零是输入要素，列1是输出变量或因变量。我们将使用列0使用上面的直线公式预测列1。

(2) 将第1列与第0列相对应。

输入变量和输出变量之间的关系是线性的。当关系为线性时，线性回归效果最佳。

(3) 初始化theta值。我正在将theta值初始化为零。但是任何其他值也应该起作用。

theta = [0,0] 

(4) 根据前面讨论的公式定义假设和成本函数。

def hypothesis(theta, X):  
    return theta[0] + theta[1]*X 
 
def cost_calc(theta, X, y):  
    return (1/2*m) * np.sum((hypothesis(theta, X) - y)**2) 

(5) 计算训练数据的数量作为DataFrame的长度。然后定义梯度下降函数。在此函数中，我们将更新theta值，直到cost函数达到最小值为止。可能需要任何数量的迭代。在每次迭代中，它将更新theta值，并使用每个更新的theta值来计算成本以跟踪成本。

m = len(df) 
def gradient_descent(theta, X, y, epoch, alpha): 
    cost = [] 
    i = 0 
    while i < epoch: 
        hx = hypothesis(theta, X) 
        theta[0] -= alpha*(sum(hx-y)/m) 
        theta[1] -= (alpha * np.sum((hx - y) * X))/m 
        cost.append(cost_calc(theta, X, y)) 
        i += 1 
    return theta, cost 

(6) 最后，定义预测函数。它将从梯度下降函数获得更新的theta并预测假设或预测的输出变量。

def predict(theta, X, y, epoch, alpha): 
    theta, cost = gradient_descent(theta, X, y, epoch, alpha) 
    return hypothesis(theta, X), cost, theta 

(7) 使用预测函数，找到假设，成本和更新的theta值。我选择学习率为0.01，然后将这个算法运行2000个时期或迭代。

y_predict, cost, theta = predict(theta, df[0], df[1], 2000, 0.01) 

最终theta值为-3.79和1.18。

(8) 在同一图中绘制原始y和假设或预测y。

%matplotlib inline 
import matplotlib.pyplot as plt 
plt.figure() 
plt.scatter(df[0], df[1], label = 'Original y') 
plt.scatter(df[0], y_predict, label = 'predicted y') 
plt.legend(loc = "upper left") 
plt.xlabel("input feature") 
plt.ylabel("Original and Predicted Output") 
plt.show() 

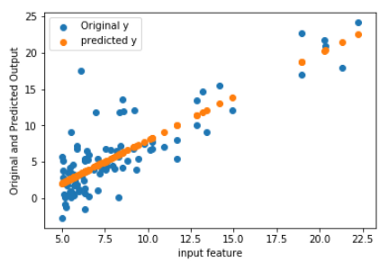
假设图是公式中所预期的一条直线，并且该直线正在最佳位置通过。

(9) 记住，我们在每次迭代中都跟踪成本函数。让我们绘制成本函数。

plt.figure() 
plt.scatter(range(0, len(cost)), cost) 
plt.show() 

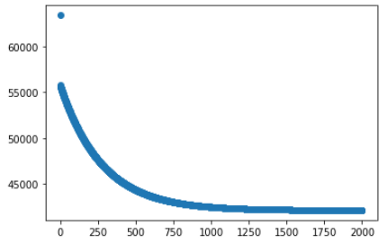
如前所述，我们的目的是优化theta值以最小化成本。从该图可以看出，成本从一开始就急剧下降，然后稳定下来。这意味着theta值已按照我们的预期正确优化。

想要获取更多Python学习资料可以加
QQ:2955637827私聊
或加Q群630390733
大家一起来学习讨论吧！