梯度提升树 Gradient Boosting Decision Tree

Adaboost + CART

用 CART 决策树来作为 Adaboost 的基础学习器

但是问题在于，需要把决策树改成能接收带权样本输入的版本。（need: weighted DTree(D, u^(t)) ）

这样可能有点麻烦，有没有简单点的办法？尽量不碰基础学习器内部，想办法在外面把数据送进去的时候做处理，能等价于给输入样本权重。（boostrapping）

例如权重 u 的占比是30%的样本，对应的 sampling 的概率就设定为 0.3。

每一个基础学习器在整体模型中的重要性还是用 α_t 来衡量（g_t 在 G 中的系数）。另外，这个方法中仍然是 boosting， CART 一定不能太强（剪枝比较多、简单点就限制树高度；训练每棵树都只用一部分训练数据）

极端情况，限制树的高度只有1，那就直接退化成 decision stump ，也就不用做 sampling 了（因为几乎不会只用 stump 就能让 error rate = 0）

GBDT

梯度提升树（GBDT）也是一种前向分步算法，但基础模型限定了使用 CART 回归树。在学习过程中，第 t 轮迭代的目标是找到一个 CART 回归树 g_t(x) 让本轮的损失函数 L(y, G_t(x)) = L(y, G_t-1(x) + g_t(x)) 尽量小。

从 Adaboost 到 general boosting

负梯度拟合的优势就是可以在通用框架下拟合各种损失误差，这样分类回归都能做。在 ensemble https://www.cnblogs.com/chaojunwang-ml/p/11208164.html 分析过，这里再回顾一遍。

统一每次更新样本权重的形式（g_t-1(x) 正确分类的样本权重减小，错误分类的样本权重增加）

那么根据递推公式，u_n^T+1 可以从 u_n¹ 推得，而表达式中正好可以发现 G(x) 的 logit（voting score）。

而 y_n * voting score 可以理解为点到分割平面的一种距离衡量，类似于 SVM 中的 margin，只不过没有归一化。而模型的训练目标就是想要让 margin 正的越大越好，等价于让 u_n^T+1 越小越好。也就是说，adaboost 中所有样本的 u_n 之和会随着时间步推移越来越小（让每一个点的 margin 都越来越正、越来越大）。

这样就可以看出 adaboost 整体模型的要最小化的目标函数，是所有时间步的所有样本权重之和，即0/1损失函数的upper bound（指数损失函数）。

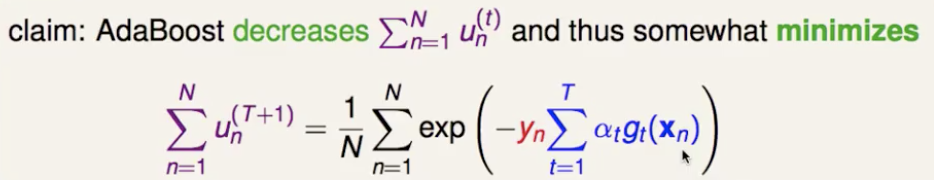
就用梯度下降（泰勒一阶展开）来实现这个最小化（不同的是，这里要求 loss 函数对 g_t(x) 函数的梯度，approximate functional gradient）。把1/N拿进去，紫色部分凑成 u_n^t ，对剩下的exp部分用泰勒公式一阶逼近，整理得到最终要对 h 求梯度的目标函数。

那就来看一下，发现最小化整体模型的目标函数，就等价于最小化 E_in^u(t) ，就是要优化基础分类器（也就是说，adaboost中前向分步训练基础分类器，其实正是在为整体模型的梯度下降优化找最好的g_t(x) ）

再来就是要确定学习率，能不能每步都找到一个最好的学习率（短期内比固定的学习率下降的快）？steepest descent：loss 对其求导并另为0。得到的最好的学习率，正是 adaboost 中的 α_t

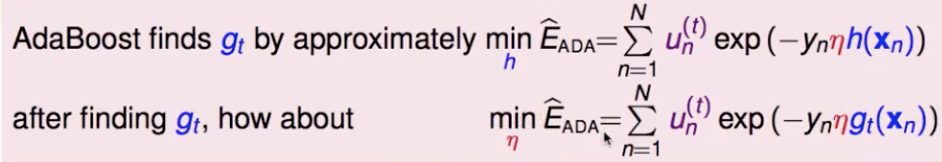
从梯度下降的角度再次总结 adaboost 做分类

gradient boosting

负梯度拟合的扩展，不只用指数损失函数，用其他的损失函数（符合平滑条件）也可以。从目前已经达到的 G(x_n) ，向某一个方向（h(x_n)）走一小步（η），使得新的 logit 与给定的 y_n 之间的某种 error 变小。

以平方误差举例，error = (s-y)²

如果在某处往某个方向走了一小步，就要乘上 gradient 在那个地方的分量（error 对 s 偏微分，在s_n 处取值）。然后就是找一个 h，让下面式子的第二项越小越好（第一项与h无关）。直接的想法是：如果 s-y 是正的，就给一个负的 h ；如果 s-y 是负的，就给一个正的 h 。那么就让 h 取到 s-y 的负方向。

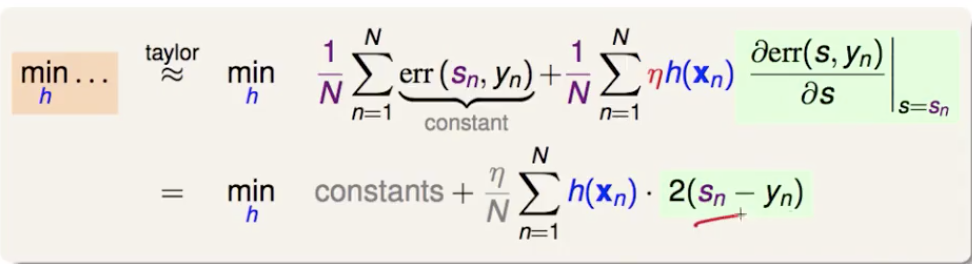
但 h 的大小呢？如果不加约束，h(x_n) = - ∞ * (s_n-y_n) ，可是我们这里找 h 只是要找一个方向，所以步长靠 η 决定。加一个正则化惩罚项即可。然后凑一个 (h(x_n) - (y_n - s_n))² 出来，配上一个和 h 无关的常数项。要最小化这个式子，就是要令 h(x_n) 和 (y_n - s_n) 之间的均方误差最小，那就是以残差 residual 为目标训练一个回归器。

然后决定 η 的大小，单变量最优化问题。但这里除了求偏微分令其等于0，还有一种简洁的求法。把 g_t(x_n) 看成是feature，residual 看成简单线性回归的目标， 求这个一维的权重。

optimal η 的解为

加入 CART 作为 base learner，总结一下 GBDT

关于 GBDT 做分类的详解：https://www.cnblogs.com/pinard/p/6140514.html