排序算法：归并排序（Merge Sort）

归并排序

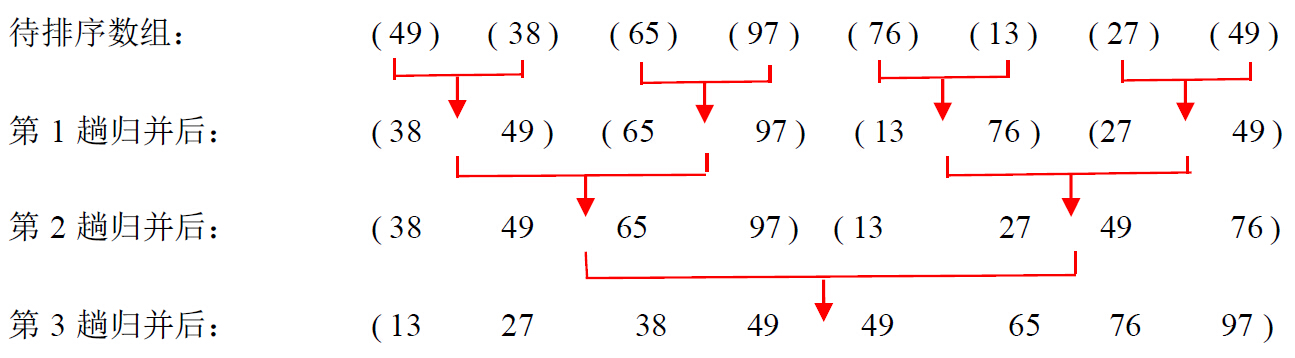
归并排序采用了分治策略（divide-and-conquer），就是将原问题分解为一些规模较小的相似子问题，然后递归解决这些子问题，最后合并其结果作为原问题的解。

归并排序将排序数组A[1..n]分成两个各含n/2个元素的子序列，然后对这个两个子序列进行递归排序，最后将这两个已排序的子序列进行合并，即得到最终排好序的序列：

**归并排序的时间复杂度为：O（nlgn），其中 MERGE(a,b,c,d)的时间复杂度为O（n）。**如果这二组组内的数据都是有序的，那么就可以很方便的将这二组数据进行排序。

• 将n个元素分成各含有n/2个元素的子序列.
• 对两个子序列递归排序.
• 合并两个已排序的子序列以得到排序结果.

 1 void merge(int x,int y){
 2     if(x==y)return;
 3     int mid=(x+y)/2,i=x,j=mid+1,k=x;
 4     merge(x,mid),merge(mid+1,y);
 5     while(i<=mid&&j<=y){
 6         if(a[i]<=a[j]){
 7             c[k++]=a[i++];
 8         }else{
 9             c[k++]=a[j++],ans+=mid-i+1;
10         }
11     }
12     while(i<=mid)c[k++]=a[i++];
13     while(j<=y)c[k++]=a[j++];
14     for(int l=x;l<=y;l++){
15         a[l]=c[l];
16     }
17 } 

归并排序的缺点：不是原地排序，需要额外申请空间来进行排序。

逆序数对求数

给定包含n个不同元素的数组A[1..n]，如果i < j且A[i] > A[j]，则(i, j)称为数组A的一个逆序。数组包含所有逆序的数量成为数组的逆序数。例对于数组[1, 2, 3, 4, 5]，它的逆序有(2, 1), (3, 1), (5, 4), (5, 1), (4, 1)，所以该数组的逆序数为5。

这里如果用冒泡排序绝对会RE,所以归并排序。可以看出，消除逆序的操作发生在while循环中：每执行一次循环体都会消除一个逆序。当所有逆序都被消除后，就完成了插入排序。所以，可以通过在插入排序中加入计数计算数组逆序数。

原数组的逆序数是两个子数组逆序数之和加上合并过程中消除的逆序数。

 1 while(i <= mid && j <= r){
 2         if(a[i] > a[j]){
 3             ans += mid - i + 1;
 4             b[t++] = a[j];
 5             ++j;
 6         }else{
 7             b[t++] = a[i];
 8             ++i;
 9         }
10 }
11     

建议输入速度更快比如快读。