洛谷 P3694 邦邦的大合唱站队 状压DP

题目描述

输入输出样例

输入 #1 复制

12 4

1

3

2

4

2

1

2

3

1

1

3

4

输出 #1 复制

7

说明/提示

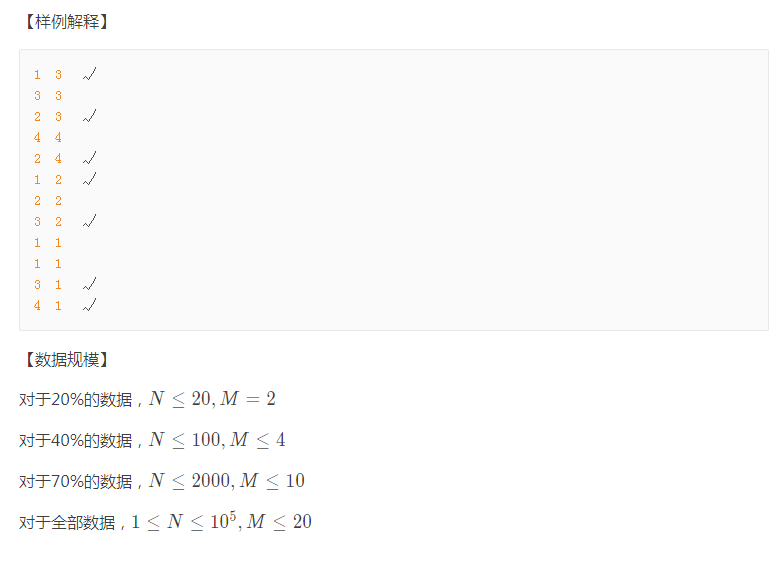
分析

首先要注意合唱队排好队之后不一定是按\(1.2.3......m\)的顺序的

\(N\)的范围很大，但\(m\)的数据比较小，所以我们考虑装压DP

我们设\(f[i]\)为状态为\(i\)的合唱队已经安排好位置的最小花费

接下来就是状态转移方程的问题

for(int i=1;i<(1<<m);i++){
        int len=0;
        for(int j=1;j<=m;j++){
            if(i&(1<<(j-1))) len+=num[j];
        }
        for(int j=1;j<=m;j++){
            if(i&(1<<(j-1))) f[i]=min(f[i],f[i^(1<<(j-1))]+num[j]-sum[len][j]+sum[len-num[j]][j]);
        }
    }

第一维枚举的是状态，在枚举状态之后，我们还要统计当前状态下哪些合唱队已经排好了位置

我们用一个变量\(len\)记录排好队的总人数，如果当前合唱队已经排好了队，那么我们把总人数加上当前合唱队的人数

其中，编号为\(j\)的合唱队的总人数\(num[j]\)可以预处理

为什么这样做呢？

因为我们无论让偶像们怎么出队，他们最终的状态是确定的，肯定是一个合唱队的偶像站到一起，因此我们就可以统计排好队后当前区间的总长度

接下来就是状态转移

如果编号为\(j\)的合唱队在我们决策的范围之内，那我们就需要尝试将编号为\(j\)的合唱队的全体成员都放在队伍最后

那么此时我们就需要将编号为\(j\)的合唱队中不在区间\([len-num[j]+1,num[j]]\)的偶像移到该区间

此时的花费为\(num[j]-sum[len][j]+sum[len-num[j]][j]\)

其中\(sum[i][j]\)表示开始时前\(i\)个位置中编号为\(j\)的合唱队员的个数

问题就可以解决了

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=22,maxm=1e5+5;
int f[1<<maxn];
int num[maxn],sum[maxm][maxn];
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        int aa;
        scanf("%d",&aa);
        num[aa]++;
        for(int j=1;j<=m;j++) sum[i][j]=sum[i-1][j];
        sum[i][aa]++;
    }
    memset(f,0x3f,sizeof(f));
    f[0]=0;
    for(int i=1;i<(1<<m);i++){
        int len=0;
        for(int j=1;j<=m;j++){
            if(i&(1<<(j-1))) len+=num[j];
        }
        for(int j=1;j<=m;j++){
            if(i&(1<<(j-1))) f[i]=min(f[i],f[i^(1<<(j-1))]+num[j]-sum[len][j]+sum[len-num[j]][j]);
        }
    }
    printf("%d\n",f[(1<< m)-1]);
    return 0;
}