7.28 NOI模拟赛 H2O 笛卡尔树 并查集 贪心 长链剖分

LINK：H2O

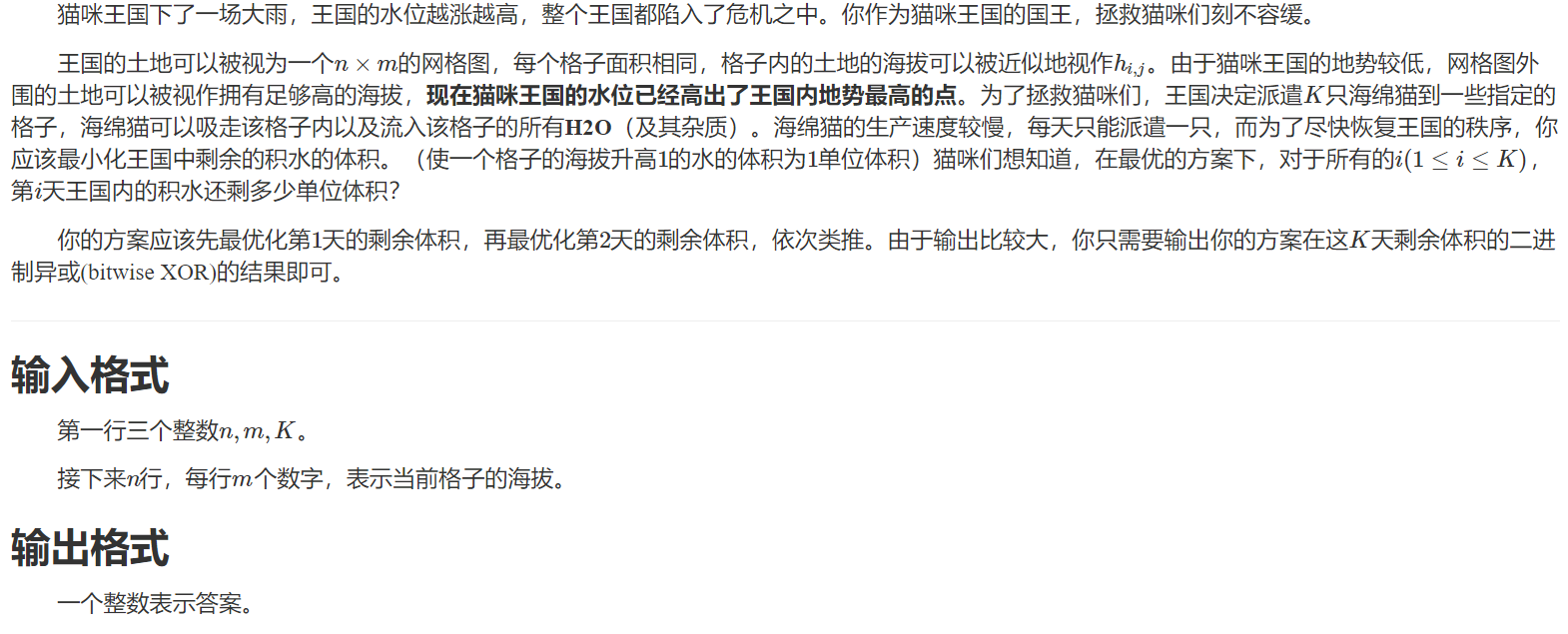
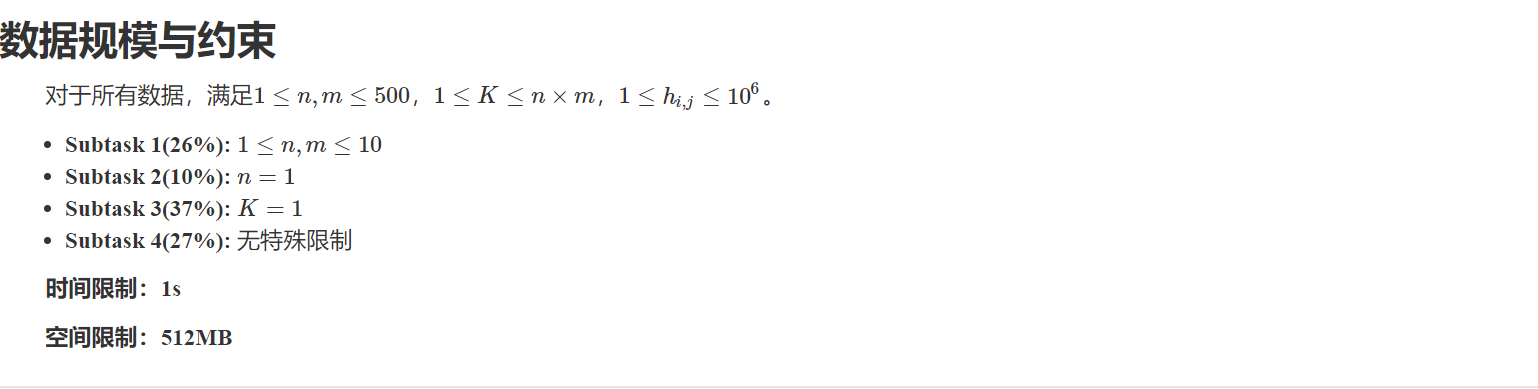
这场比赛打的稀烂 爆蛋.

只会暴力.感觉暴力细节比较多不想写.

其实这道题的难点就在于 采取什么样的策略放海绵猫.

知道了这一点才能确定每次放完海绵猫后的答案.

暴力枚举是不行的。而我们又想不到怎么做？

此时需要考虑一维的情况 化简问题 在数轴上进行贪心.

可以发现全局最大值挡住了左右两边 也就是说左右两边是完全独立的。

继续思考 递归左边此时区间全局最大值也是如此.

一个容易观察到的是 l和r相邻 较大的那个一定在较小之后选择.

那么其实就是递归所有的地方来比较 从而进行选择.

删掉之后带来的影响 其实是一路递归下来的树的影响.

其实就是笛卡尔树了 进一步发现每个节点和父亲的边删掉都会有权值 这样是我们进行第一次删掉时的答案的体现.

从而发现第一次删掉是最长链 那么就可以长链剖分维护贪心了.

考虑二维的情况.

我们还是考虑把树建立出来进行长链剖分.

怎么建树 全局最大值肯定为根节点.

然后选出全局次大的节点进行连边 类比一下即可.

值得注意的是 正着做有联通块什么的会不断分裂。反着就可以用并查集合并.

排序之后反着做就可以把树建出来了.

笛卡尔树的建立也要学会 最近遇到的比较多了！

code

//#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<ctime>
#include<cctype>
#include<queue>
#include<deque>
#include<stack>
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<cstring>
#include<string>
#include<ctime>
#include<cmath>
#include<cctype>
#include<cstdlib>
#include<queue>
#include<deque>
#include<stack>
#include<vector>
#include<algorithm>
#include<utility>
#include<bitset>
#include<set>
#include<map>
#define ll long long
#define db double
#define INF 1000000000
#define inf 100000000000000000ll
#define ldb long double
#define pb push_back
#define put_(x) printf("%d ",x);
#define get(x) x=read()
#define gt(x) scanf("%d",&x)
#define gi(x) scanf("%lf",&x)
#define put(x) printf("%d\n",x)
#define putl(x) printf("%lld\n",x)
#define rep(p,n,i) for(RE int i=p;i<=n;++i)
#define go(x) for(int i=lin[x],tn=ver[i];i;tn=ver[i=nex[i]])
#define fep(n,p,i) for(RE int i=n;i>=p;--i)
#define vep(p,n,i) for(RE int i=p;i<n;++i)
#define pii pair<int,int>
#define mk make_pair
#define RE register
#define P 1000000007ll
#define gf(x) scanf("%lf",&x)
#define pf(x) ((x)*(x))
#define uint unsigned long long
#define ui unsigned
#define EPS 1e-10
#define sq sqrt
#define S second
#define F first
#define mod 1000000007
#define id(i,j) ((i-1)*m+j)
#define max(x,y) ((x)<(y)?y:x)
using namespace std;
char *fs,*ft,buf[1<<15];
inline char gc()
{
	return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
	RE int x=0,f=1;RE char ch=gc();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=gc();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=gc();}
	return x*f;
}
const int MAXN=510,maxn=MAXN*MAXN;
int n,m,top,rt,k,len,num;
int a[maxn],f[MAXN],son[MAXN],sz[MAXN];
ll c[MAXN],mx[MAXN],ans,cnt;
int lin[maxn],ver[maxn],nex[maxn];
inline void add(int x,int y)
{
	ver[++len]=y;
	nex[len]=lin[x];
	lin[x]=len;
}
priority_queue<ll>q;
inline int getfather(int x){return x==f[x]?x:f[x]=getfather(f[x]);}
struct wy
{
	int x,y;
	int z;
	inline bool operator <(wy a)const{return z<a.z;}
}t[maxn];
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
inline void dfs(int x)
{
	sz[x]=1;
	go(x)
	{
		dfs(tn);
		c[tn]=(ll)(a[x]-a[tn])*sz[tn];
		ans+=c[tn];mx[tn]+=c[tn];
		if(mx[tn]>mx[x])
		{
			mx[x]=mx[tn];
			son[x]=tn;
		}
		sz[x]+=sz[tn];
	}
}
inline void dp(int x,int fa)
{
	if(x==fa)q.push(mx[x]);
	if(son[x])dp(son[x],fa);
	go(x)if(tn!=son[x])dp(tn,tn);
}
int main()
{
	//freopen("1.in","r",stdin);
	get(n);get(m);get(k);
	rep(1,n,i)rep(1,m,j)
	{
		int get(x);
		f[id(i,j)]=id(i,j);
		t[++num]=(wy){i,j,x};
	}
	//cout<<id(1,2)<<endl;
	sort(t+1,t+1+num);
	//cout<<t[1].z<<endl;
	rep(1,num,i)
	{
		int x=t[i].x;
		int y=t[i].y;
		int id=id(x,y);
		rep(0,3,k)
		{
			int xx=dx[k]+x;
			int yy=dy[k]+y;
			if(xx<1||yy<1||xx>n||yy>m)continue;
			if(!a[id(xx,yy)])continue;
			int w1=getfather(id(xx,yy));
			if(w1==id)continue;
			f[w1]=id;add(id,w1);
		}
		a[id]=t[i].z;
	}
	rt=id(t[num].x,t[num].y);
	//put(rt);
	//cout<<getfather(1)<<endl;
	dfs(rt);dp(rt,rt);
	while(q.size()&&k)
	{
		ans-=q.top();
		cnt=cnt^ans;
		q.pop();--k;
	}
	putl(cnt);
	return 0;
}