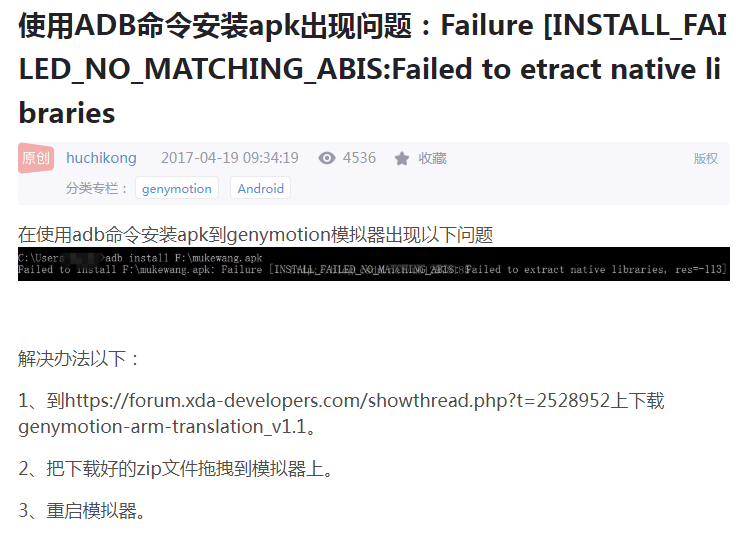
图片摘自CSDN，待验证

adb命令装包failure问题的更多相关文章

  1. ADB命令详解及大全（ 声明：此文是参考大佬博客所做的笔记！）

    adb是什么? adb的全称为Android Debug Bridge,就是起到调试桥的作用.通过adb我们可以在Eclipse中方面通过DDMS来调试Android程序,说白了就是debug工具.a ...

  2. [整理]ADB命令行学习笔记

    global driver# 元素定位driver.find_element_by_id("id") # id定位driver.find_element_by_name(" ...

  3. 玩转ADB命令（ADB命令使用大全）转载

    ADB是什么 Adb的全称为Android Debug Bridge:android调试桥梁,下图为Android官方对adb的介绍:可以看出,Android的初衷是用adb这样的一个工具来协助开发人 ...

  4. 最全的ADB命令行大全（转）

    基本用法 命令语法 adb 命令的基本语法如下: adb [-d|-e|-s ] 如果只有一个设备/模拟器连接时,可以省略掉 [-d|-e|-s ] 这一部分,直接使用 adb . 为命令指定目标设备 ...

  5. 分享一个常用Adb命令

    分享一个常用Adb命令 首先 首先感谢@xuxu的常用adb命令,收益良多,但是已经不能满足于我,所以补充了下. 再者 好久没发帖了,最近论坛老司机们都在讨论/总结,我就用这个干货回报吧. 最后 基于 ...

  6. Android命令之-------ADB命令大全

    1.显示当前运行的全部模拟器:    adb devices2.启动ADB    adb start-server3.停止ADB   adb kill-server4.安装应用程序:      adb ...

  7. adb环境配置+常用adb命令+Logcat命令的用法+手动进行文件比对的方法+批量挪bug

    1. adb环境配置:下载adb环境变量包:打开计算机属性-高级系统设置-环境变量:新建变量adb,值为刚才的环境变量包路径:编辑path值,在最后面加上;%adb%;确定就妥了 2. 常用adb命令 ...

  8. 常用 ADB 命令[ZZ]

    https://blog.csdn.net/yang_zhang_1992/article/details/71404186 1. 显示当前运行的全部模拟器: adb devices 2. 对某一模拟 ...

  9. android调试工具adb命令大全

    转载: 一.adb介绍SDK的Tools文件夹下包含着Android模拟器操作的重要命令adb,adb的全称为(Android Debug Bridge就是调试桥的作用.通过adb我们可以在Eclip ...

随机推荐

  1. Jmeter 常用函数（14）- 详解 __strLen

    如果你想查看更多 Jmeter 常用函数可以在这篇文章找找哦 https://www.cnblogs.com/poloyy/p/13291704.htm 作用 读取给定字符串的长度 语法格式 ${__ ...

  2. SparkSQL DSL 随便写写

    @Testdef functionTest() = { Logger.getLogger("org").setLevel(Level.WARN) val spark = getSp ...

  3. 微信公众号请求code时报redirect_uri 参数错误

    (1) 检查微信公众号中"接口权限"--"网页授权获取用户基本信息"中的网页授权域名.域名不带http(s) (2)如果在拼接跳转到微信授权接口的URL时,使用 ...

  4. WSGI 配置禁止反向DNS查找

    原文链接:https://opendev.org/starlingx/ha/src/commit/045a37c672a92f1412629a176f51183c88882e61/service-mg ...

  5. Mac本软件安装之后打不开的解决办法

    Mac本软件安装之后打不开的解决办法 MacOS系统版本10.15.3 一,安装Axure RP 9 问题:安装之后打不开 提示“Axure RP 9已损坏,无法打开”或“打不开 Axure RP 9 ...

  6. Intelligence Beyond the Edge: Inference on Intermittent Embedded Systems

    郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布! 以下是对本文关键部分的摘抄翻译,详情请参见原文. Abstract 能量收集技术为未来的物联网应用提供了一个很有前景的平台.然而,由于这些 ...

  7. 数组的三种方式总结 多维数组的遍历 Arrays类的常用方法总结

    一.数组的三种声明方式总结 public class WhatEver { public static void main(String[] args) { //第一种 例: String[] tes ...

  8. asyncio异步模块的21个协程编写实例

    启动一个无返回值协程 通过async关键字定义一个协程 import sys import asyncio async def coroutine(): print('运行协程') if sys.ve ...

  9. 喵的Unity游戏开发之路 - 在球体上行走

    很多童鞋没有系统的Unity3D游戏开发基础,也不知道从何开始学.为此我们精选了一套国外优秀的Unity3D游戏开发教程,翻译整理后放送给大家,教您从零开始一步一步掌握Unity3D游戏开发. 本文不 ...

  10. seo快速排名利器之高权重二级域名

    http://www.wocaoseo.com/thread-225-1-1.html        正规的白帽手法优化一个关键词一般都需要两三个月才能把词做上去,但是现在也有一批做网站优化的采取特殊 ...