牛客练习赛71 C.数学考试 (DP,容斥原理)

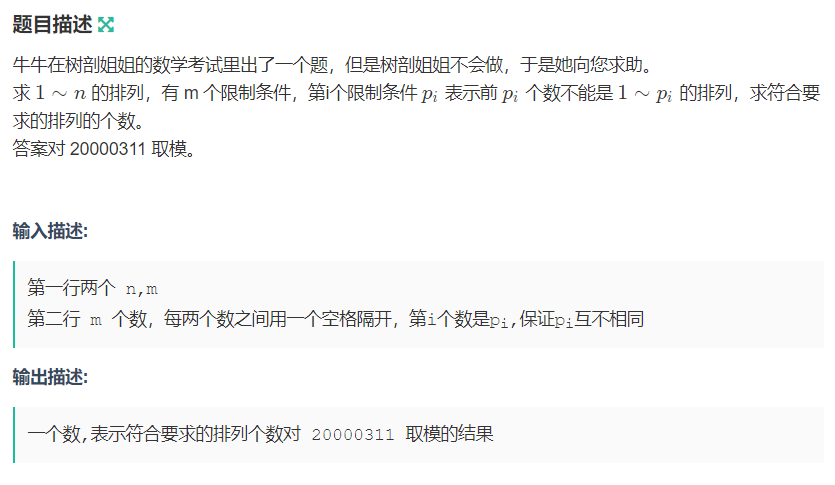
• 题意:RT

• 题解:先对\(p\)排个序,然后设\(dp[i]\)表示前\(i-1\)个\(p[i]\)满足条件但是\(p[i]\)不满足,即在\([1,p[i]]\)中不存在从\(p[1]\)到\(p[i-1]\)[的排列,比如说\(p[1]=1\),\(p[2]=2\),\(p[3]=3\),则\(dp[4]\)中一定不能存在\([1,x,x,x](p[1])\),\([1,2,x,x](p[2])\),\([1,2,3,x]\)这样的序列,因为这些对于\(p[1]\)到\(p[i-1]\)存在不满足的情况,但是像\([4,3,2,1]\)这样的就可以,所以我们按这个思路想,先假设\(dp[i]=A_{p[i]}^{p[i]}\),可以推出公式,\(dp[i]=dp[i]-\sum_{j=1}^{i-1}(dp[j]*(fac[p[i]-p[j]]))\),求出所有的\(dp\)数组之后,我们就可以计算答案了,和求\(dp\)的公式类似,我们用所有的情况\(n!\)减去每个独立的限制条件\(p[i]\)的情况,所以\(ans=n!-\sum_{i=1}^{n}(dp[i]*(fac[n-p[i]]))\).记得取模.

• 代码:

  int n,m;
  ll p[N];
  ll fac[N];
  ll dp[N];
  
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
      cin>>n>>m;
      fac[0]=1;
      for(int i=1;i<=m;++i){
          cin>>p[i];
      }
      for(int i=1;i<=n;++i){
          fac[i]=fac[i-1]*i%mod;
      }
      sort(p+1,p+1+m);
      dp[1]=fac[p[1]];
  
      for(int i=2;i<=m;++i){
          dp[i]=fac[p[i]];
          for(int j=1;j<i;++j){
              dp[i]=(dp[i]-dp[j]*fac[p[i]-p[j]])%mod;
          }
      }
  
      ll ans=fac[n];
  
      for(int i=1;i<=m;++i){
          ans=(ans-dp[i]*fac[n-p[i]])%mod;
      }
      cout<<(ans%mod+mod)%mod<<endl;
      return 0;
  }