Codeforces Round #650 (Div. 3) F1. Flying Sort (Easy Version) (离散化,贪心)

• 题意:有一组数,每次操作可以将某个数移到头部或者尾部,问最少操作多少次使得这组数非递减.

• 题解:先离散化将每个数映射为排序后所对应的位置,然后贪心,求最长连续子序列的长度,那么最少的操作次数一定为\(n-len\).

  感觉不好解释,直接上图,其实就是排序后它们一定是连续的,所以我们就求一个最长的连续的,然后s剩下的数移到头部尾部,贪心的想,这样一定是最优解.

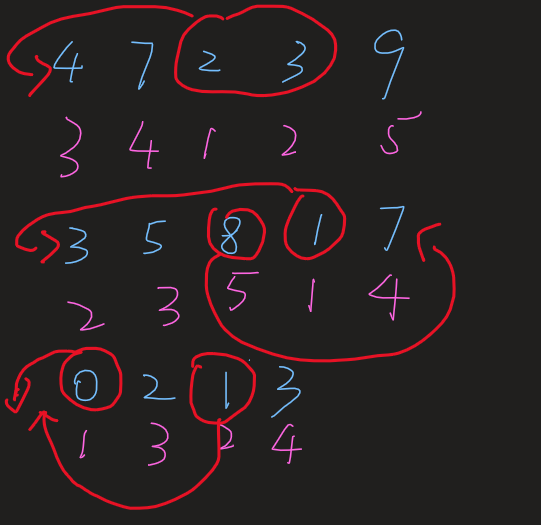
• 代码:

  #include <iostream>
  #include <cstdio>
  #include <cstring>
  #include <cmath>
  #include <algorithm>
  #include <stack>
  #include <queue>
  #include <vector>
  #include <map>
  #include <set>
  #include <unordered_set>
  #include <unordered_map>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  const int N = 1e6 + 10;
  const int mod = 1e9 + 7;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  
  int t;
  int n;
  int a[N];
  int b[N];
  
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);
  	cin>>t;
  	 while(t--){
  	 	cin>>n;
  	 	 for(int i=1;i<=n;++i){
  	 	 	cin>>a[i];
  	 	 	b[i]=a[i];
  	 	 }
          sort(b+1,b+1+n);
          for(int i=1;i<=n;++i){
          	a[i]=lower_bound(b+1,b+1+n,a[i])-b;
          }
          int ans=0;
          int cnt=1;
          while(cnt<=n){
          	int len=0;
          	for(int i=1;i<=n;++i){
          		if(a[i]==cnt){
          			cnt++,len++;
          		}
          	}
          	ans=max(ans,len);
          }
  
          cout<<n-ans<<endl;
       }
      return 0;
  }