C语言实现表达式求值，支持+、-、*、/四则运算，并且支持多级括号，自定义了栈的操作。

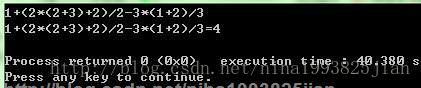
以下是代码的实现使用gcc已经成功运行了，下面是效果图

#include <stdio.h>
#include <stdlib.h>

#define OPT_ADD 43 /* + */
#define OPT_SUB 45 /* - */
#define OPT_MUL 42 /* * */
#define OPT_DIV 47 /* / */
#define L_BRACK 40 /* ( */

typedef struct _stack
{
  int  data; /* 栈内元素 */
  struct _stack *next;
}Stack; /* 定义栈结构! */

/**
* 压栈
* 头插法,将数据压到头结点
**/
int push_stack(Stack **stack, int data)
{
  Stack *p = (Stack*)malloc(sizeof(Stack));
  if (NULL == p)
    exit(-1); /* 申请内存都不行,挂了 */
  p->data = data;
  p->next = *stack;
  *stack = p;
  return 0;
}

/**
* 弹栈
* 头指针就是栈顶
**/
int pop_stack(Stack **stack)
{
  Stack *p = *stack;  /* 缓存头指针 */
  if (NULL == p)
    return -1;        /* 栈已经空了 */
  int data = p->data; /* 缓存栈顶数据 */
  *stack  = p->next;  /* 栈顶移动  */
  free(p);            /* 释放内存  */
  return data;
}

/**
* 获取栈顶元素
**/
int get_top_stack(Stack *stack)
{
  return stack->data; /* 头指针就是栈顶 */
}

/**
* 判断栈空
**/
int stack_is_empty(Stack *stack)
{
  return NULL == stack ? 1 : 0;
}

/**
* 栈内元素个数
**/
int count_stack(Stack *stack)
{
  int cnt = 0;
  while (NULL != stack)
  {
    cnt++;
    stack = stack->next;
  }
  return cnt;
}

/**
* 销毁栈
**/
void destroy_stack(Stack **stack)
{
  Stack *p = *stack, *q;
  while (NULL != p)
  {
    q = p->next;
    free(p);
    p = q;
  }
  *stack = NULL;
}

/**
* 显示所有栈元素
**/
void show_stack(const char *name, Stack *stack)
{
  printf("[%s: ", name);
  while (NULL != stack)
  {
    printf("%d,", stack->data);
    stack = stack->next; /* 从栈顶依次打印 */
  }
  printf("]\n");
}

/**
* 计算a和b在mode符号的运算结果
**/
int cal(int a,int b,int mode)
{
  int re = -1;
  switch(mode)
  {
  case OPT_ADD: re = a + b; break;
  case OPT_SUB: re = a - b; break;
  case OPT_MUL: re = a * b; break;
  case OPT_DIV: re = a / b; break;
  default: break;
  }
  return re;
}

/**
* 符号优先级判断
* 返回： 1(opt1>opt2) -1(opt1<opt2) 0(opt1=opt2)
* 注意符号的ASSIC码：43(+) 45(-) 42(*) 47(/)
**/
int opt_max(int opt1,int opt2)
{
  if(OPT_MUL == opt1 || OPT_DIV == opt1)
  {
    if(OPT_ADD == opt2 || OPT_SUB == opt2)
    {
      return 1;
    }
  }
  else
  {
    if(OPT_MUL == opt2 || OPT_DIV == opt2)
    {
      return -1;
    }
  }
  return 0;
}

/**
* 计算表达式
**/
int calculate(const char *expr)
{
  int num1, num2, opt1, opt2;
  Stack *num = NULL;
  Stack *opt = NULL;
  while ('\0' != *expr)
  {
    if ('(' == *expr)
    { /* 左括号 */
      push_stack(&opt, (int)*expr++); /* 压符号栈 */
    }
    else if (')' == *expr)
    { /* 右括号 */
      expr++; /* 指针加1 */
      while (1)
      {
        if (L_BRACK == get_top_stack(opt))
        {
          pop_stack(&opt);
          break; /* 如果当前栈顶是(则弾栈退出 */
        }
        else
        { /* 否则弾两个数字，一个符号进行运算 */
          num2 = pop_stack(&num);
          num1 = pop_stack(&num);
          opt2 = pop_stack(&opt);
          push_stack(&num, cal(num1, num2, opt2));
        }
      }
    }
    else if ('9' >= *expr && '0' <= *expr)
    { /* 数字 */
      sscanf(expr, "%d", &num1);
      push_stack(&num, num1);
      num2 = 0;     /* 记录num1的长度 */
      while (0 != num1) {num2++; num1 /= 10;}
      expr += num2; /* 指针移动指定长度 */
    }
    else if (*expr == OPT_ADD || *expr == OPT_SUB || *expr == OPT_MUL || *expr == OPT_DIV)
    { /* 加减乘除,这4个符号 */
      opt1 = (int)*expr++;
      while (1)
      {
        if (stack_is_empty(opt) || L_BRACK == get_top_stack(opt))
        {
          push_stack(&opt, opt1);
          break;
        }
        else
        {
          opt2 = get_top_stack(opt);
          if (0 < opt_max(opt1, opt2))
          { /* 当前获取的符号优先级大于栈顶符号 */
            push_stack(&opt, opt1);
            break;
          }
          else
          { /* 栈顶优先级高或者平级 */
            num2 = pop_stack(&num);
            num1 = pop_stack(&num);
            opt2 = pop_stack(&opt);
            push_stack(&num, cal(num1, num2, opt2));
          }
        }
      }
    } else {
      printf("expression error\n");
      num1 = -1; /* 这种是表达式错误 */
      goto MUST_END;
    }
  }

  num1 = count_stack(num);
  num2 = count_stack(opt);
  if (num1 == 3 && num2 == 2) {
    num2 = pop_stack(&num);
    num1 = pop_stack(&num);
    opt2 = pop_stack(&opt); /* 剩余3个数字和2个操作符,需要多计算一次 */
    push_stack(&num, cal(num1, num2, opt2));
  } else if (num1 == 2 && num2 == 1) {
    /* 剩余2个数字和1个操作符,最后只计算1次 */
  } else {
    printf("expression error\n");
    num1 = -1; /* 这种是表达式错误 */
    goto MUST_END;
  }
  num2 = pop_stack(&num);
  num1 = pop_stack(&num);
  opt2 = pop_stack(&opt);
  num1 = cal(num1, num2, opt2);

MUST_END:
  destroy_stack(&num); /* 销毁num栈 */
  destroy_stack(&opt); /* 销毁opt栈 */
  return num1;
}

/**
* 主程序
* 放在最下面,避免重复声明函数
**/
int main(int argc, char *argv[])
{
  if (argc == 2) {
    printf("%s=%d\n", argv[1], calculate(argv[1]));
  } else {
    printf("usage:%s expression\n", argv[0]);
  }
  return 0;
}

至于原理嘛栈的操作我就不多叙述了。主要讲讲算法的事情，首先计算函数开始的时候就创建了数字栈和符号栈。处理的时候把所有字符串里取出来的东西都在栈里用整形保存，这样可以统一数字栈和符号栈是同种结构。当遍历字符串时遇到数字字符就把当前开始的数字取出来压数字栈，当遇到左括号是总是压符号栈不管连续多少个左括号，当遇到右括号时就从数字栈和符号栈中取值计算并从新压栈，直到遇到左括号，期间还要比较运算符的优先级等。当遇到字符串结束时还没有计算完成，此时数字栈和字符栈内都有值。如果数字栈为3个，符号栈为2个那么要计算两次，如果数字栈为2个，符号栈为1个计算一次。最终得出结果。我写这个程序时思路还是清晰的，就是不知道有没有小问题，希望能给大家一些启发。测试出问题也希望大家给我说，大家一起进步嘛。