数据结构与算法：AVL树

AVL树

在计算机科学中，AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它。

平衡因子：某结点的左子树与右子树的高度(深度)差即为该结点的平衡因子

AVL树的特点：

本身首先是一棵二叉搜索树。
带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。

也就是说，AVL树，本质上是带了平衡功能的二叉查找树（二叉排序树，二叉搜索树）

为什么需要平衡树？

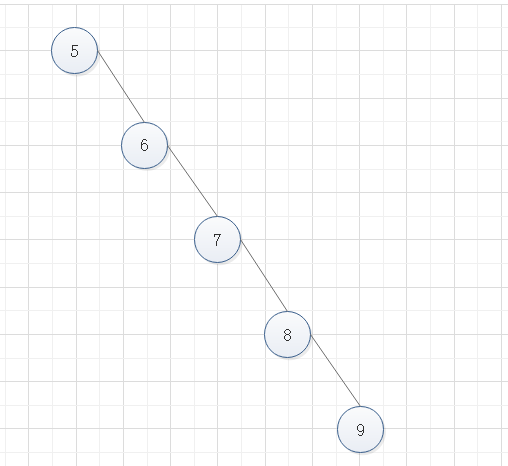
举个极端的例子：当我们将一个数组 [5, 6, 7, 8, 9]转换成二叉排序树时，它的二叉树图会如下图所示。

可以看出这时二叉树趋近于链表，虽然它的插入和删除的效率不会受到影响，但是查找的效率就有所降低了，因为它和链表一样需要从头到尾查找。

AVL树的旋转操作

AVL树的旋转操作有三种：

当右子树的高度高于左子树一层以上时进行的左旋转
当左子树的高度高于右子树一层以上时进行的右旋转
以及特殊情况下进行的双向旋转。

左旋转

当二叉排序树的某一节点的右子树的高度高于左子树一层以上时，为了平衡二叉树排序树，需要对二叉排序树进行左旋转操作。

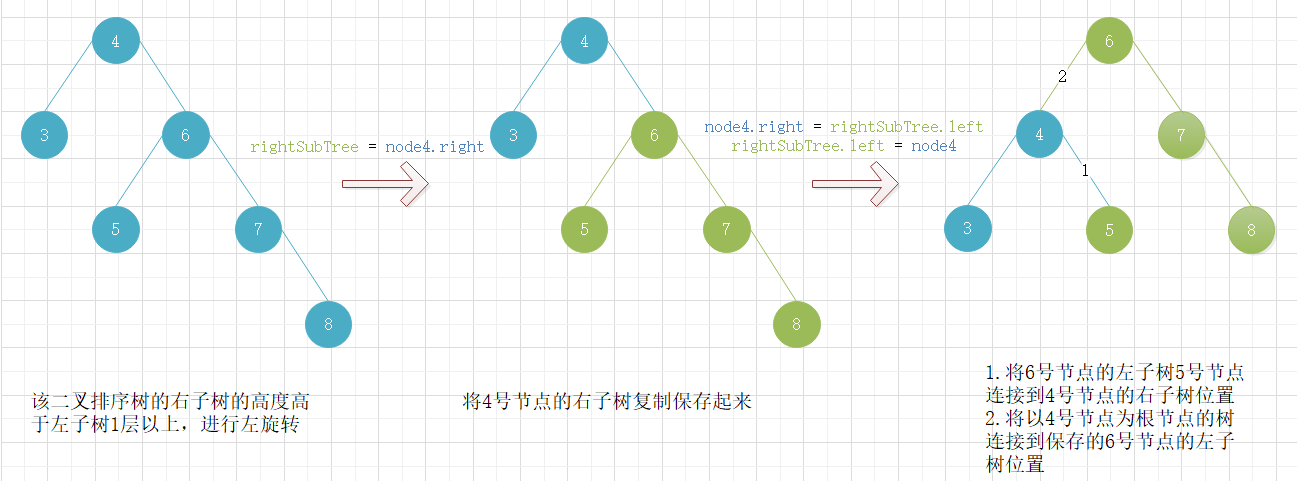
右旋转

当二叉排序树的某一节点的左子树的高度高于右子树一层以上时，为了平衡二叉树排序树，需要对二叉排序树进行右旋转操作。

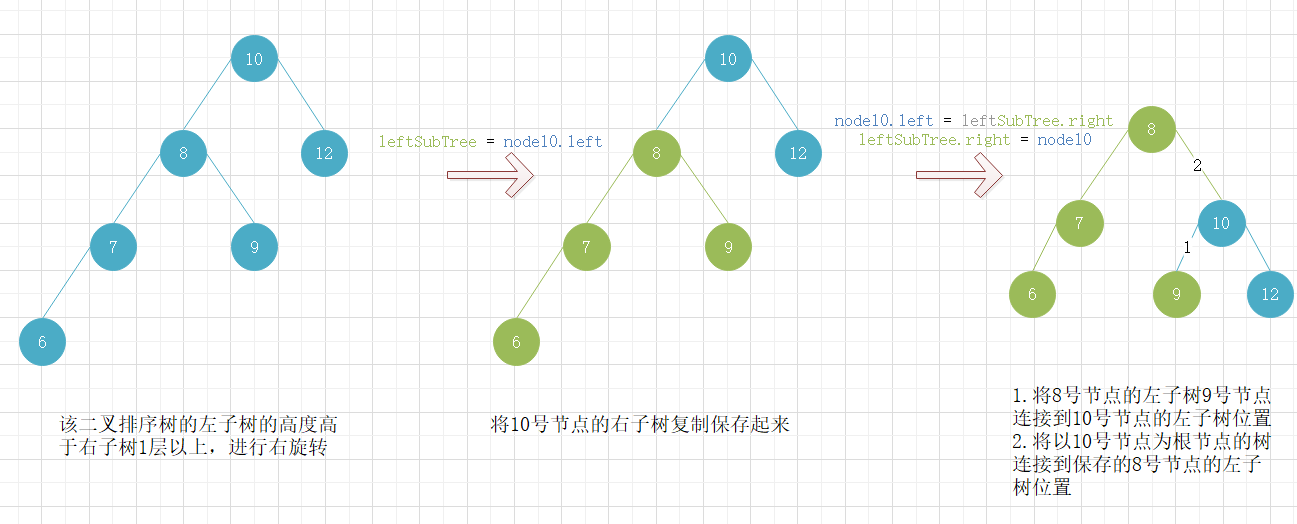
双向旋转

在进行左旋转或右旋转时需要判断一个特殊情况。如下图所示，根节点的左子树高度高于右子树一层以上，即平衡因子大于1，随即对该二叉树排序树进行右旋转操作，可以看出右旋转后根节点右子树的高度高于左子树一层以上，平衡因子还是大于1，二叉排序树的平衡问题还是没解决。

观察该二叉排序树可以发现，根节点的左子节点8号节点的右子树的高度是高于左子树的，但只大于1，所以没有进入到旋转平衡操作，当我们为根节点下的子树进行右旋转时，会将8号节点较高的右子树连接到10号节点上，这时以10号节点为根节点的树高度就高于8号节点的左子树2层了，而随后我们又将该树来连接到8号节点的右子树上，就导致了旋转后平衡因子还是大于1的问题。

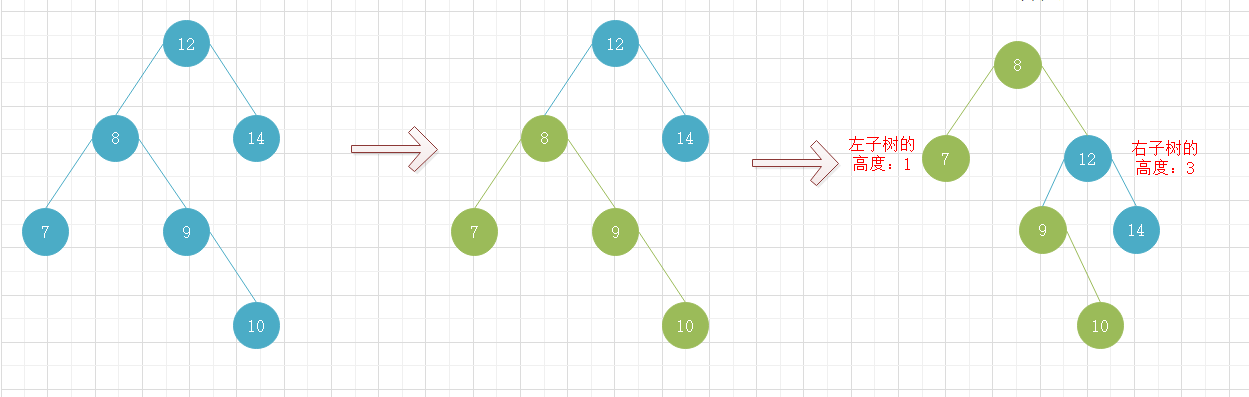
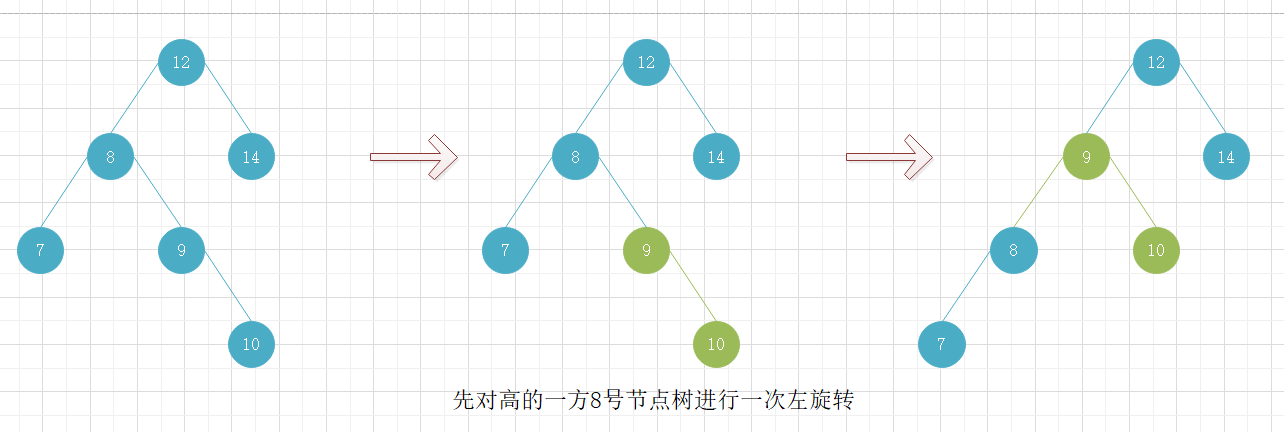
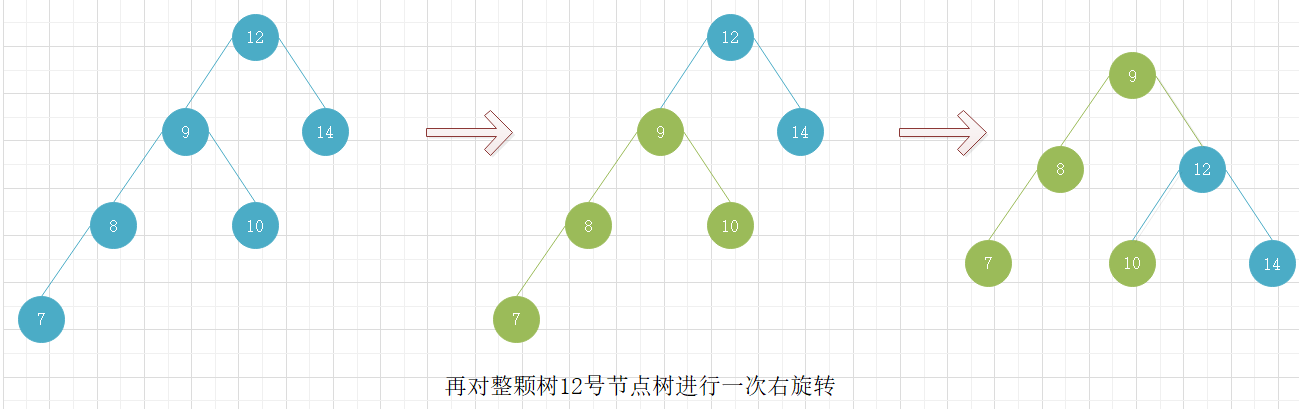
所以在遇到上面这种情况，即左旋转时右子树的左子树高于右子树的右子树或右旋转时左子树的右子树高于左子树的左子树，需先对较高的子树树进行一次右旋转或左旋转，再对整颗树进行左旋转或右旋转。

下图是当右旋转时左子树的右子树高于左子树的左子树的情况。

代码实现

获取树的高度

在进行旋转前，需要先判断以该节点为根节点的树是否需要进行旋转平衡，而判断是否需要旋转得知道该节点的左子树和右子树的高度。

//获取该节点左子树的高度
public int leftHeight(){
    if (this.left == null){
        return 0;
    }
    return this.left.height();
}
 
//获取该节点右子树的高度
public int rightHeight(){
    if (this.right == null){
        return 0;
    }
    return this.right.height();
}
 
//获取以该节点为根节点的树的高度
public int height(){
    /*
    Math.max方法可以取出俩个参数中的最大值，因为是递归叠加，所以需+1，
    如当该节点是叶子节点时，如果不+1的话，会返回0，导致该节点没有被算入高度中
     */
    return Math.max(this.left==null ? 0:this.left.height(), this.right==null ? 0:this.right.height()) + 1;
}

旋转操作

//左旋转
public AVLNode leftRotate(){
    //保存该节点的右子树
    AVLNode rightSubTree = this.right;
    //将该节点的右子树 替换成 保存的右子树rightSubTree的左子树
    this.right = rightSubTree.left;
    //再把以该节点为根节点的树 连接到 rightSubTree的左子树
    rightSubTree.left = this;
    //最后返回左旋转后新的树
    return rightSubTree;
}
 
//右旋转
public AVLNode rightRotate(){
    AVLNode leftSubTree = this.left;
    this.left = leftSubTree.right;
    leftSubTree.right = this;
    return leftSubTree;
}

在进行完上面步骤后，还需要进行关键的一步，把旋转后返回的新树连接到该节点在旋转前的父节点，因为本来以该节点为根节点的树经过旋转后根节点发生了变化，不再是该节点，所以需要用旋转后新树的根节点去替代旋转前该节点位置。

在进行连接父节点操作时，还需注意旋转前该节点是整颗二叉排序树中一颗子树的根节点还是整颗二叉排序树的根节点。

添加操作中的平衡判断：

/**
* 在二叉排序树中添加节点
* @param node 添加的节点
* @param pointer 指针节点，用于遍历节点，初始指向根节点
* @return 返回添加后平衡的新树
*/
public AVLNode add(AVLNode node, AVLNode pointer){
    if (node == null){
        return null;
    }
 
    if (pointer.value > node.value){//指针节点值大于添加节点值时
        //如果指针节点的左节点刚好为空，则将添加节点插入到该左节点
        if (pointer.left == null){
            pointer.left = node;
        }else {
            //如果不是则继续往左节点走
            pointer.left = add(node, pointer.left);
        }
    }else {//指针节点值小于添加节点值时
        //如果指针节点的右节点刚好为空，则将添加节点插入到该右节点
        if (pointer.right == null){
            pointer.right = node;
        }else {
            //如果不是则继续往右节点走
            pointer.right = add(node, pointer.right);
        }
    }
 
    //添加完节点后，判断以该节点为根节点的树是否平衡，如不平衡则需进行旋转
    if (rightHeight(pointer) - leftHeight(pointer) > 1){//判断节点的右子树高度是否比左子树高过1层以上
        //当左旋转时，需判断右子树的左子树高度是否高于右子树的右子树
        if (leftHeight(pointer.right) > rightHeight(pointer.right)){
            //当满足上面条件时，则需双向旋转
            //先对右子树进行右旋转
            AVLNode rightSubTree = rightRotate(pointer.right);
            //将右旋转后新的右子树连接到该节点的右子树位置
            pointer.right = rightSubTree;
            //再对以该节点为根节点的树进行左旋转
            pointer = leftRotate(pointer);
        }else {
            //如果不满足条件，则直接左旋转
            pointer = leftRotate(pointer);
        }
    }else if (leftHeight(pointer) - rightHeight(pointer) > 1) {//判断节点的左子树高度是否比右子树高过1层以上
        //当右旋转时，需判断左子树的右子树高度是否高于左子树的左子树
        if (rightHeight(pointer.left) > leftHeight(pointer.left)) {
            //当满足上面条件时，则需双向旋转
            //先对左子树进行左旋转
            AVLNode leftSubTree = leftRotate(pointer.left);
            //将左旋转后新的左子树连接到该节点的左子树
            pointer.left = leftSubTree;
            //再对以该节点为根节点的树进行右旋转
            pointer = rightRotate(pointer);
        } else {
            //如果不满足条件，则直接右旋转
            pointer = rightRotate(pointer);
        }
    }
    return pointer;
}

然后将原先的二叉排序树更新为添加后经过平衡的新的AVL二叉排序树

//添加节点
public void add(AVLNode node){
    //如果根节点为空则，则将传入节点设置为根节点
    if (root == null){
        root = node;
    }else {
        root = add(node, root);
    }
}

删除操作中的平衡判断：

/**
 * 根据value值删除节点
 * 删除节点可能有的3种状态：
 * 1.该节点是叶子节点
 * 2.该节点只有左子树或只有右子树
 * 3.该节点左子树和右子树都有
 * @param value 要删除节点的value值
 */
public AVLNode delete(int value, AVLNode node){
    AVLNode delRes = null;//储存删除后新的树
    if (value < node.value){//当查找节点值小于当前节点值
        //向左子树递归遍历，并将删除后的新的左子树连接到左节点位置代替原先左子树
        node.left = delete(value, node.left);
        //删除后新的树
        delRes =  node;
    }else if(value > node.value){//当查找节点值大于当前节点值
        //向右子树递归遍历，并将删除后的新的右子树连接到右节点位置代替原先右子树
        node.right = delete(value, node.right);
        //删除后新的树
        delRes =  node;
    }else {//当查找节点值等于当前节点值时，即当前节点就是要删除的节点
        //删除节点时叶子节点的状态
        if (node.left == null && node.right == null) {
            //直接将该节点设为空
            //当该节点为空时，无需进入到后面的平衡判断，直接返回
            return null;
        }
        //删除节点左子树为空，右子树不为空的状态
        else if (node.left == null && node.right != null) {
            //保存删除节点的右子树
            AVLNode rightSubTree = node.right;
            //将删除节点的右子树设为空，使得该节点能够尽早被垃圾回收
            node.right = null;
            //删除节点的右子树，用于连接到删除节点的父节点
            delRes = rightSubTree;
        }
        //删除节点右子树为空，左子树不为空的状态
        else if (node.right == null && node.left != null) {
            AVLNode leftSubTree = node.left;
            node.left = null;
            delRes = leftSubTree;
        }
        //删除节点的左子树和右子树都不为空的状态
        //这里我们使用的是左子树的最大值节点代替的方法
        else {
            //获取左子树的最大值节点并从左子树中删除它
            AVLNode max = max(node.left);
            //将该最大值节点的左子树和右子树设置为该节点的左子树和右子树
            //注：删除最大值节点操作的返回值是删除后该节点的左子树
            max.left = delMax(node.left);
            max.right = node.right;
            //将删除节点的左子树和右子树设为空，使得该节点能够尽早被垃圾回收
            node.left = null;
            node.right = null;
            //执行完删除操作后，以最大值节点为根节点的新的树，用于连接的删除节点的父节点
            delRes = max;
        }
    }
 
    //删除节点后要判断删除后的新的树是否平衡，如不平衡需进行旋转操作
    if (rightHeight(delRes) - leftHeight(delRes) > 1){
        if (leftHeight(delRes.right) > rightHeight(delRes.right)){
            AVLNode rightSubTree = rightRotate(delRes.right);
            node.right = rightSubTree;
            return leftRotate(delRes);
        }else {
            return leftRotate(delRes);
        }
    }else if (leftHeight(delRes) - rightHeight(delRes) > 1) {
        if (rightHeight(delRes.left) > leftHeight(delRes.left)) {
            AVLNode leftSubTree = leftRotate(delRes.left);
            delRes.left = leftSubTree;
            return rightRotate(delRes);
        } else {
            return rightRotate(delRes);
        }
    }
    //返回删除后的新树
    return delRes;
}
 
/**
* 查找传入节点树下value值最大的节点并删除该节点
* @param node
* @return
*/
public AVLNode delMax(AVLNode node){
    if (node.right != null){
        node.right = delMax(node.right);
        return node;
    }else {
        AVLNode leftSubTree = node.left;
        node.left = null;
        return leftSubTree;
    }
}
/**
* 查找传入节点树下value值最大的节点并放回该节点
* 在二叉排序树中最大值的节点就是最右叶子节点
* @param node
* @return
*/
public AVLNode max(AVLNode node){
    AVLNode max = node;
    while (max.right != null){
        max = max.right;
    }
    return max;
}

同样也需要将原先的二叉排序树更新为删除后经过平衡的AVL二叉排序树

//删除节点
public void delete(int value){
    //判断删除节点在二叉排序树中是否存在
    AVLNode node = searchNode(value);
    if (node == null){
        throw new RuntimeException("二叉排序树内无对应节点");
    }
    //将删除后新的二叉排序树更换掉原先二叉排序树
    root = delete(value, root);
}

完整代码

public class AVLTreeDemo {
    public static void main(String[] args) {
        AVLTree avlTree = new AVLTree();
        int[] array = {4,3,6,5,7,8};//左旋转
        //int[] array = {10,12,8,9,7,6};//右旋转
        //int[] array = {10,11,7,6,8,9};//双向旋转
        for (int i : array){
            avlTree.add(new AVLNode(i));
        }
 
        System.out.println("leftHeight: " + avlTree.leftHeight(avlTree.root));
        System.out.println("rightHeight" + avlTree.rightHeight(avlTree.root));
        avlTree.midOrder();
    }
}
 
//AVL二叉排序树
class AVLTree{
    AVLNode root;
 
    public void setRoot(AVLNode root){
        this.root = root;
    }
 
    //左旋转
    public AVLNode leftRotate(AVLNode node){
        //保存该节点的右子树
        AVLNode rightSubTree = node.right;
        //将该节点的右子树 替换成 保存的右子树rightSubTree的左子树
        node.right = rightSubTree.left;
        //再把以该节点为根节点的树 连接到 rightSubTree的左子树
        rightSubTree.left = node;
        //最后返回左旋转后新的树
        return rightSubTree;
    }
 
    //右旋转
    public AVLNode rightRotate(AVLNode node){
        AVLNode leftSubTree = node.left;
        node.left = leftSubTree.right;
        leftSubTree.right = node;
        return leftSubTree;
    }
 
    //获取该节点左子树的高度
    public int leftHeight(AVLNode node){
        if (node.left == null){
            return 0;
        }
        return height(node.left);
    }
 
    //获取该节点右子树的高度
    public int rightHeight(AVLNode node){
        if (node.right == null){
            return 0;
        }
        return height(node.right);
    }
 
    //获取以该节点为根节点的树的高度
    public int height(AVLNode node){
        /*
        Math.max方法可以取出俩个参数中的最大值，因为是递归叠加，所以需+1，
        如当该节点是叶子节点时，如果不+1的话，会返回0，导致该节点没有被算入高度中
         */
        return Math.max(node.left==null ? 0:height(node.left), node.right==null ? 0:height(node.right)) + 1;
    }
 
    //添加节点
    public void add(AVLNode node){
        //如果根节点为空则，则将传入节点设置为根节点
        if (root == null){
            root = node;
        }else {
            root = add(node, root);
        }
    }
 
    /**
     * 在二叉排序树中添加节点
     * @param node 添加的节点
     * @param pointer 指针节点，用于遍历节点，初始指向根节点
     * @return 返回添加后平衡的新树
     */
    public AVLNode add(AVLNode node, AVLNode pointer){
        if (node == null){
            return null;
        }
 
        if (pointer.value > node.value){//指针节点值大于添加节点值时
            //如果指针节点的左节点刚好为空，则将添加节点插入到该左节点
            if (pointer.left == null){
                pointer.left = node;
            }else {
                //如果不是则继续往左节点走
                pointer.left = add(node, pointer.left);
            }
        }else {//指针节点值小于添加节点值时
            //如果指针节点的右节点刚好为空，则将添加节点插入到该右节点
            if (pointer.right == null){
                pointer.right = node;
            }else {
                //如果不是则继续往右节点走
                pointer.right = add(node, pointer.right);
            }
        }
 
        //添加完节点后，判断以该节点为根节点的树是否平衡，如不平衡则需进行旋转
        if (rightHeight(pointer) - leftHeight(pointer) > 1){//判断节点的右子树高度是否比左子树高过1层以上
            //当左旋转时，需判断右子树的左子树高度是否高于右子树的右子树
            if (leftHeight(pointer.right) > rightHeight(pointer.right)){
                //当满足上面条件时，则需双向旋转
                //先对右子树进行右旋转
                AVLNode rightSubTree = rightRotate(pointer.right);
                //将右旋转后新的右子树连接到该节点的右子树位置
                pointer.right = rightSubTree;
                //再对以该节点为根节点的树进行左旋转
                pointer = leftRotate(pointer);
            }else {
                //如果不满足条件，则直接左旋转
                pointer = leftRotate(pointer);
            }
        }else if (leftHeight(pointer) - rightHeight(pointer) > 1) {//判断节点的左子树高度是否比右子树高过1层以上
            //当右旋转时，需判断左子树的右子树高度是否高于左子树的左子树
            if (rightHeight(pointer.left) > leftHeight(pointer.left)) {
                //当满足上面条件时，则需双向旋转
                //先对左子树进行左旋转
                AVLNode leftSubTree = leftRotate(pointer.left);
                //将左旋转后新的左子树连接到该节点的左子树
                pointer.left = leftSubTree;
                //再对以该节点为根节点的树进行右旋转
                pointer = rightRotate(pointer);
            } else {
                //如果不满足条件，则直接右旋转
                pointer = rightRotate(pointer);
            }
        }
        return pointer;
    }
 
    //根据value值查找节点
    public AVLNode searchNode(int value){
        if (root == null){
            return null;
        }
        return searchNode(value, root);
    }
 
    /**
     * 根据value值查找节点
     * @param value 查找的节点
     * @param node 查找的树
     * @return
     */
    public AVLNode searchNode(int value, AVLNode node){
        //如果当前节点的值等于value时，则返回该节点
        if (node.value == value) {
            return node;
        } else if (node.value > value){//当前节点的值大于value时
            //如果该节点的左节点为空，则表示二叉排序树内没有该值的节点，返回空
            if (node.left == null)
                return null;
            //左节点不为空，继续往左子树查找
            return searchNode(value, node.left);
        }else {//当前节点的值小于value时
            //如果该节点的右节点为空，则表示二叉排序树内没有该值的节点，返回空
            if (node.right == null)
                return null;
            //右节点不为空，继续往右子树查找
            return searchNode(value, node.right);
        }
    }
 
    public void delete(int value){
        //判断删除节点在二叉排序树中是否存在
        AVLNode node = searchNode(value);
        if (node == null){
            throw new RuntimeException("二叉排序树内无对应节点");
        }
        //将删除后新的二叉排序树更换掉原先二叉排序树
        root = delete(value, root);
    }
 
    /**
     * 根据value值删除节点
     * 删除节点可能有的3种状态：
     * 1.该节点是叶子节点
     * 2.该节点只有左子树或只有右子树
     * 3.该节点左子树和右子树都有
     * @param value 要删除节点的value值
     */
    public AVLNode delete(int value, AVLNode node){
        AVLNode delRes = null;//储存删除后新的树
        if (value < node.value){//当查找节点值小于当前节点值
            //向左子树递归遍历，并将删除后的新的左子树连接到左节点位置代替原先左子树
            node.left = delete(value, node.left);
            //删除后新的树
            delRes =  node;
        }else if(value > node.value){//当查找节点值大于当前节点值
            //向右子树递归遍历，并将删除后的新的右子树连接到右节点位置代替原先右子树
            node.right = delete(value, node.right);
            //删除后新的树
            delRes =  node;
        }else {//当查找节点值等于当前节点值时，即当前节点就是要删除的节点
            //删除节点时叶子节点的状态
            if (node.left == null && node.right == null) {
                //直接将该节点设为空
                //当该节点为空时，无需进入到后面的平衡判断，直接返回
                return null;
            }
            //删除节点左子树为空，右子树不为空的状态
            else if (node.left == null && node.right != null) {
                //保存删除节点的右子树
                AVLNode rightSubTree = node.right;
                //将删除节点的右子树设为空，使得该节点能够尽早被垃圾回收
                node.right = null;
                //删除节点的右子树，用于连接到删除节点的父节点
                delRes = rightSubTree;
            }
            //删除节点右子树为空，左子树不为空的状态
            else if (node.right == null && node.left != null) {
                AVLNode leftSubTree = node.left;
                node.left = null;
                delRes = leftSubTree;
            }
            //删除节点的左子树和右子树都不为空的状态
            //这里我们使用的是左子树的最大值节点代替的方法
            else {
                //获取左子树的最大值节点并从左子树中删除它
                AVLNode max = max(node.left);
                //将该最大值节点的左子树和右子树设置为该节点的左子树和右子树
                //注：删除最大值节点操作的返回值是删除后该节点的左子树
                max.left = delMax(node.left);
                max.right = node.right;
                //将删除节点的左子树和右子树设为空，使得该节点能够尽早被垃圾回收
                node.left = null;
                node.right = null;
                //执行完删除操作后，以最大值节点为根节点的新的树，用于连接的删除节点的父节点
                delRes = max;
            }
        }
 
        //删除节点后要判断删除后的新的树是否平衡，如不平衡需进行旋转操作
        if (rightHeight(delRes) - leftHeight(delRes) > 1){
            if (leftHeight(delRes.right) > rightHeight(delRes.right)){
                AVLNode rightSubTree = rightRotate(delRes.right);
                node.right = rightSubTree;
                return leftRotate(delRes);
            }else {
                return leftRotate(delRes);
            }
        }else if (leftHeight(delRes) - rightHeight(delRes) > 1) {
            if (rightHeight(delRes.left) > leftHeight(delRes.left)) {
                AVLNode leftSubTree = leftRotate(delRes.left);
                delRes.left = leftSubTree;
                return rightRotate(delRes);
            } else {
                return rightRotate(delRes);
            }
        }
        //返回删除后的新树
        return delRes;
    }
 
    /**
     * 查找传入节点树下value值最大的节点并删除该节点
     * @param node
     * @return
     */
    public AVLNode delMax(AVLNode node){
        if (node.right != null){
            node.right = delMax(node.right);
            return node;
        }else {
            AVLNode leftSubTree = node.left;
            node.left = null;
            return leftSubTree;
        }
    }
    /**
     * 查找传入节点树下value值最大的节点并放回该节点
     * 在二叉排序树中最大值的节点就是最右叶子节点
     * @param node
     * @return
     */
    public AVLNode max(AVLNode node){
        AVLNode max = node;
        while (max.right != null){
            max = max.right;
        }
        return max;
    }
 
    public void midOrder(){
        if (root != null){
            midOrder(root);
        }else {
            System.out.println("二叉顺序树为空，无法遍历");
        }
    }
 
    //中序遍历
    public void midOrder(AVLNode node){
        if (node.left != null){
            midOrder(node.left);
        }
        System.out.println(node);
        if (node.right != null){
            midOrder(node.right);
        }
    }
}
 
//AVL二叉排序树节点
class AVLNode{
    int value;
    AVLNode left;
    AVLNode right;
 
    public AVLNode(int value){
        this.value = value;
    }
 
    @Override
    public String toString() {
        return "BSTNode{" +
                "value=" + value +
                '}';
    }
}