C语言实现数据结构的邻接矩阵----数组生成矩阵、打印、深度优先遍历和广度优先遍历

写在前面

　　图的存储结构有两种：一种是基于二维数组的邻接矩阵表示法。

　　　　　　　　　　　　另一种是基于链表的的邻接表表示法。

　　在邻接矩阵中，可以如下表示顶点和边连接关系：

　　　　

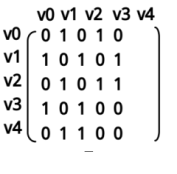
说明：

　　将顶点对应为下标，根据横纵坐标将矩阵中的某一位置值设为1，表示两个顶点向联接。

　　图示表示的是无向图的邻接矩阵，从中我们可以发现它们的分布关于斜对角线对称。

　　我们在下面将要讨论的是下图的两种遍历方法（基于矩阵的）：

　　　　

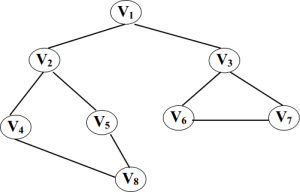
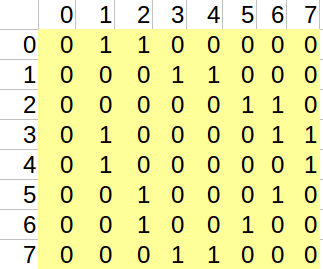
　　我们已经说明了我们要用到的是邻接矩阵表示法，那么我首先要来构造图：

1.深度优先遍历算法

　　分析深度优先遍历

　　　　从图的某个顶点出发，访问图中的所有顶点，且使每个顶点仅被访问一次。这一过程叫做图的遍历。

　　　　深度优先搜索的思想：

　　　　　　①访问顶点v；

　　　　　　②依次从v的未被访问的邻接点出发，对图进行深度优先遍历；直至图中和v有路径相通的顶点都被访问；

　　　　　　③若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。

　　　　比如：

　　　　

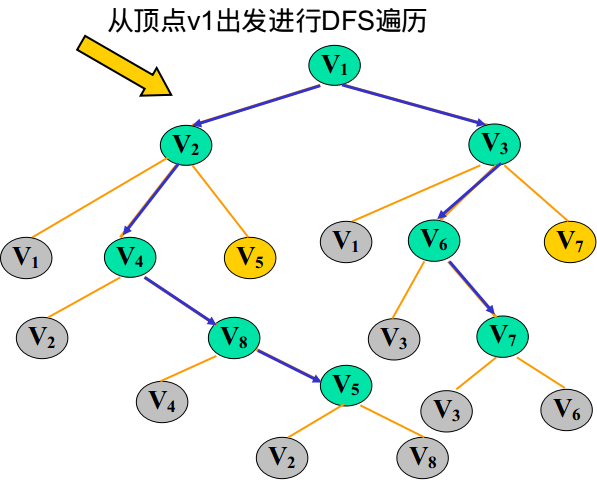
　　　　在这里为了区分已经访问过的节点和没有访问过的节点，我们引入一个一维数组bool visited[MaxVnum]用来表示与下标对应的顶点是否被访问过，

流程：

☐ 首先输出 V1，标记V1的flag=true;

☐ 获得V1的邻接边 [V2 V3],取出V2，标记V2的flag=true;

☐ 获得V2的邻接边[V1 V4 V5],过滤掉已经flag的，取出V4，标记V4的flag=true;

☐ 获得V4的邻接边[V2 V8],过滤掉已经flag的，取出V8，标记V8的flag=true;

☐ 获得V8的邻接边[V4 V5],过滤掉已经flag的，取出V5，标记V5的flag=true;

☐ 此时发现V5的所有邻接边都已经被flag了，所以需要回溯。（左边黑色虚线，回溯到V1，回溯就是下层递归结束往回返）

☐ 

☐ 回溯到V1，在前面取出的是V2，现在取出V3，标记V3的flag=true;

☐ 获得V3的邻接边[V1 V6 V7]，过滤掉已经flag的,取出V6，标记V6的flag=true;

☐ 获得V6的邻接边[V3 V7],过滤掉已经flag的,取出V7，标记V7的flag=true;

☐ 此时发现V7的所有邻接边都已经被flag了，所以需要回溯。（右边黑色虚线，回溯到V1，回溯就是下层递归结束往回返）

　　深度优先搜索的代码

2.广度优先搜索算法

　　分析广度优先遍历　　　　

　　　　所谓广度，就是一层一层的，向下遍历，层层堵截，还是这幅图，我们如果要是广度优先遍历的话，我们的结果是V1 V2 V3 V4 V5 V6 V7 V8。

　　　　　　

　　　　广度优先搜索的思想：

　　　　　 　① 访问顶点vi ；

　　　　　　 ② 访问vi 的所有未被访问的邻接点w1 ,w2 , …wk ；

　　　　　　 ③ 依次从这些邻接点（在步骤②中访问的顶点）出发，访问它们的所有未被访问的邻接点; 依此类推，直到图中所有访问过的顶点的邻接点都被访问；

　　　说明：

　　　　　　为实现③，需要保存在步骤②中访问的顶点，而且访问这些顶点的邻接点的顺序为：先保存的顶点，其邻接点先被访问。 这里我们就想到了用标准模板库中的queue队列来实现这种先进现出的服务。

　　　　　　老规矩我们还是走一边流程：

　　　说明：　

　　　　 ☐将V1加入队列，取出V1，并标记为true(即已经访问)，将其邻接点加进入队列，则 <—[V2 V3]　

　　　　 ☐取出V2，并标记为true(即已经访问)，将其未访问过的邻接点加进入队列，则 <—[V3 V4 V5]

☐取出V3，并标记为true(即已经访问)，将其未访问过的邻接点加进入队列，则 <—[V4 V5 V6 V7]

☐取出V4，并标记为true(即已经访问)，将其未访问过的邻接点加进入队列，则 <—[V5 V6 V7 V8]

☐取出V5，并标记为true(即已经访问)，因为其邻接点已经加入队列，则 <—[V6 V7 V8]

☐取出V6，并标记为true(即已经访问)，将其未访问过的邻接点加进入队列，则 <—[V7 V8]

☐取出V7，并标记为true(即已经访问)，将其未访问过的邻接点加进入队列，则 <—[V8]

☐取出V8，并标记为true(即已经访问)，将其未访问过的邻接点加进入队列，则 <—[]

两种表示法：

邻接矩阵完整代码：

#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
//邻接矩阵
#define OK 1
#define ERROR 0

#define MAXNUM 10

typedef int Status;
typedef char ElemType;
typedef struct
{
    int vnum;    //顶点数
    int anum;    //弧/边数
    ElemType vex[MAXNUM];    //存储顶点
    int arc[MAXNUM][MAXNUM];    //存储边关系
}MGraph;

int Location(MGraph G, ElemType e)
{
    int v;
    for (v = 0; v<G.vnum; v++)
        if (G.vex[v] == e)return v;
    return -1;

}

Status CreateGraph(MGraph &G, int vnum, int anum, ElemType v[], ElemType a[])    //数组生成图
{
    int k;
    G.vnum = vnum;    //获取数组顶点数
    G.anum = anum;    //获取数组边数
    for (k = 0; k<G.vnum; k++)
        G.vex[k] = v[k];
    for (int i = 0; i<G.vnum; i++)
    {
        for (int j = 0; j<G.vnum; j++)
            G.arc[i][j] = 0;
    }
    int t = 0;
    int p, q;
    for (k = 0; k<G.anum; k++)
    {
        ElemType m, n;
        m = a[t++];
        n = a[t++];
        t++;
        p = Location(G, m);
        q = Location(G, n);
        G.arc[p][q] = 1;
        G.arc[q][p] = 1;
    }
    return OK;
}

void Print(MGraph G)
{
    int v;
    printf("顶点序列为:\n");
    for (v = 0; v<G.vnum; v++)
        printf("%3c", G.vex[v]);
    printf("\n");
    printf("边的二维数组关系:\n");
    for (int i = 0; i<G.vnum; i++)
    {
        for (int j = 0; j<G.vnum; j++)
            printf("%3d", G.arc[i][j]);
        printf("\n");
    }
    printf("\n");
}

int FirstAdjVex(MGraph G, int i)
{
    int v;
    if (i<0 || i >= G.vnum)return -1;
    for (v = 0; v<G.vnum; v++)
        if (G.arc[i][v] == 1)return v;
    return -1;
}

int NextAdjVex(MGraph G, int i, int j)
{
    if (i<0 || i >= G.vnum)return -1;
    if (j<0 || j >= G.vnum)return -1;
    for (int v = j + 1; v<G.vnum; v++)
        if (G.arc[i][v] == 1)return v;
    return -1;
}

//DFS遍历
int visited[MAXNUM];
void DFS(MGraph G, int v);
void DFSTraverse(MGraph G)
{
    printf("深度优先遍历为:\n");
    int v;
    for (v = 0; v<G.vnum; v++)
        visited[v] = 0;
    for (v = 0; v<G.vnum; v++)
    {
        if (visited[v] == 0)DFS(G, v);
    }
}
void DFS(MGraph G, int v)
{
    printf("%3c", G.vex[v]);
    visited[v] = 1;
    int w = FirstAdjVex(G, v);
    while (w != -1)
    {
        if (visited[w] == 0)DFS(G, w);
        w = NextAdjVex(G, v, w);
    }
}

//BFS遍历
typedef struct QNode
{
    ElemType data;
    struct QNode *next;
}QNode, *QueuePtr;    //定义队列的指针类型为QueuePtr,定义队列结点内存空间类型为QNode
typedef struct
{
    QueuePtr front;    //front为头指针，指向头结点。Q.front->next指针存在头结点的指针域(即其存着首结点的地址)，是头结点的指针，指向首结点
    QueuePtr rear;
}LinkQueue;    //定义队列结点类型为LinkQueue

Status InitQueue(LinkQueue &Q)
{
    Q.front = (QNode*)malloc(sizeof(QNode));
    if (!Q.front)return ERROR;
    Q.front->next = NULL;
    Q.rear = Q.front;
    return OK;
}

Status EnQueue(LinkQueue &Q, ElemType e)    //入队
{
    QueuePtr p;
    p = (QNode*)malloc(sizeof(QNode));    //生成新结点p
    if (!p)return ERROR;
    p->next = NULL;    //新结点的指针p->next置空
    p->data = e;    //新结点暂存e
    Q.rear->next = p;    //队尾结点的指针Q.rear->next指向新结点p
    Q.rear = p;    //队尾指针Q.rear指向p
    return OK;
}

Status DeQueue(LinkQueue &Q, ElemType &e)    //出队
{
    QueuePtr p;
    if (Q.rear == Q.front)    //确保队列有首结点
        return ERROR;
    p = Q.front->next;    //指针p暂存被删结点(首结点)的地址
    Q.front->next = p->next;    //头结点的指针Q.front->next指向首结点的下一结点
    e = p->data;
    if (Q.front->next == Q.rear)    //判断原队列是否只有首结点
        Q.rear = Q.front;
    free(p);//清空
    return OK;
}

bool EmptyQueue(LinkQueue Q)    //判空
{
    if (Q.front == Q.rear)return true;
    else return false;
}

void BFS(MGraph G)
{
    printf("广度优先遍历为:\n");
    int v;
    LinkQueue Q;
    InitQueue(Q);
    for (v = 0; v<G.vnum; v++)    //初始化
        visited[v] = 0;
    for (v = 0; v<G.vnum; v++)
    {
        if (visited[v] == 1)continue;
        printf("%3c", G.vex[v]);
        visited[v] = 1;
        EnQueue(Q, G.vex[v]);
        while (EmptyQueue == 0)
        {
            int v;
            ElemType e;
            DeQueue(Q, e);
            v = Location(G, e);
            int w = FirstAdjVex(G, v);
            while (w != -1)
            {
                w = NextAdjVex(G, v, w);
                if (visited[w] = 1)continue;
                printf("%3c", G.vex[w]);
                EnQueue(Q, G.vex[w]);
                visited[w] = 1;
            }
        }
    }
}

int main()
{
    MGraph G;
    ElemType v[] = "abcdef";    //顶点数组
    ElemType a[] = "ab,ac,ad,be,ce,df";    //边数组
    CreateGraph(G, 6, 6, v, a);
    Print(G);
    DFSTraverse(G);
    printf("\n");
    BFS(G);
    printf("\n");
    system("pause");
    return 0;
}//

邻接表完整代码：

#include<stdio.h>
#include<malloc.h>

#define OK 1
#define ERROR 0

#define MAXNUM 10

typedef int Status;
typedef char ElemType;
typedef struct ANode
{
    int adjvex;    //邻接点域
    struct ANode *next;    //邻接点指针域
}ANode;    //ANode为单链表的指针类型
typedef struct
{
    ElemType data;
    ANode *firstarc;    //定义单链表的头指针为firstarc
}VNode;    //VNode为顶点数组元素的类型
typedef struct
{
    int vnum,anum;    //顶点数，边数
    VNode vex[MAXNUM];    //顶点集
}ALGraph;    //ALGraph邻接表类型

int Location(ALGraph G, ElemType e)
{
    int v;
    for (v = 0; v<G.vnum; v++)
        if (G.vex[v].data == e)return v;
    return -1;
}

Status CreatGraph(ALGraph &G, int vnum, int anum, ElemType v[], ElemType a[])
{
    int k, t = 0;
    G.vnum = vnum;
    G.anum = anum;
    for (k = 0; k<G.vnum; k++)
    {
        G.vex[k].data = v[k];
        G.vex[k].firstarc = NULL;//易忘记
    }
    for (k = 0; k<G.anum; k++)
    {
        ElemType m, n;
        ANode *p1, *p2, *p3;
        int p, q;
        m = a[t++];
        n = a[t++];
        t++;
        p = Location(G, m);
        q = Location(G, n);
        p1 = (ANode*)malloc(sizeof(ANode));
        if (p1 == NULL)return ERROR;
        p1->adjvex = q;
        p1->next = NULL;
        if (G.vex[p].firstarc == NULL)
            G.vex[p].firstarc = p1;
        else
        {
            p3 = G.vex[p].firstarc;
            while (p3->next)
                p3 = p3->next;
            p3->next = p1;
        }
        p2 = (ANode*)malloc(sizeof(ANode));
        if (!p2)return ERROR;
        p2->adjvex = p;
        p2->next = NULL;
        if (G.vex[q].firstarc == NULL)
            G.vex[q].firstarc = p2;
        else
        {
            p3 = G.vex[p].firstarc;
            while (p3->next)
                p3 = p3->next;
            p3->next = p2;
        }

    }
    return OK;
}

int FirstAdjVex(ALGraph G, int v)
{
    if (v<0 || v >= G.vnum)return -1;
    if (G.vex[v].firstarc != NULL)
        return G.vex[v].firstarc->adjvex;
    return -1;
}

int NextAdjVex(ALGraph G, int v, int w)
{
    ANode *p;
    p = G.vex[v].firstarc;
    if (v<0 || v >= G.vnum)return -1;
    if (w<0 || w >= G.vnum)return -1;
    while (p&&p->adjvex != w)
        p = p->next;
    if (p ！= NULL || p->next ！= NULL)
        return p->next->adjvex;
    return -1;
}

//DFS
int visited[MAXNUM];
void DFS(ALGraph G, int v);
void DFSTraverse(ALGraph G)
{
    printf("深度遍历为:\n");
    int v;
    for (v = 0; v<G.vnum; v++)
        visited[v] = 0;
    for (v = 0; v<G.vnum; v++)
        if (visited[v] == 0)DFS(G, v);
    printf("\n");
}
void DFS(ALGraph G, int v)
{
    int w;
    printf("%3c", G.vex[v].data);
    visited[v] = 1;
    w = FirstAdjVex(G, v);
    while (w != -1)
    {
        if (visited[w] == 0)DFS(G, w);
        w = NextAdjVex(G, v, w);
    }

}

//BFS遍历-链队列
typedef struct QNode
{
    ElemType data;
    struct QNode *next;
}QNode, *QueuePtr;
typedef struct
{
    QueuePtr front;
    QueuePtr rear;
}LinkQueue;

Status InitQueue(LinkQueue &Q)
{
    Q.front = (QNode*)malloc(sizeof(QNode));
    if (!Q.front)return ERROR;
    Q.front->next = NULL;
    Q.rear = Q.front;
    return OK;
}
//入队
Status EnQueue(LinkQueue &Q, ElemType e)
{
    QueuePtr p;
    p = (QNode*)malloc(sizeof(QNode));
    if (!p)return ERROR;
    p->next = NULL;
    p->data = e;
    Q.rear->next = p;
    Q.rear = p;
    return OK;
}

//出队
Status DeQueue(LinkQueue &Q, ElemType &e)
{
    QueuePtr p;
    if (Q.rear == Q.front)
        return ERROR;
    p = Q.front->next;
    Q.front->next = p->next;
    if (Q.front->next == Q.rear)
        Q.rear = Q.front;
    e = p->data;
    free(p);//清空
    return OK;
}

//判空
bool EmptyQueue(LinkQueue Q)
{
    if (Q.front == Q.rear)return true;
    else return false;
}

//BFS
void BFS(ALGraph G)
{
    printf("广度优先遍历为:\n");
    int v;
    LinkQueue Q;
    InitQueue(Q);
    for (v = 0; v<G.vnum; v++)//初始化
        visited[v] = 0;
    for (v = 0; v<G.vnum; v++)
    {
        if (visited[v] == 1)continue;
        printf("%3c", G.vex[v].data);
        visited[v] = 1;
        EnQueue(Q, G.vex[v].data);
        while (EmptyQueue == 0)
        {
            int v;
            ElemType e;
            DeQueue(Q, e);
            v = Location(G, e);
            int w = FirstAdjVex(G, v);
            while (w != -1)
            {
                w = NextAdjVex(G, v, w);
                if (visited[w] = 1)continue;
                printf("%3c", G.vex[w].data);
                EnQueue(Q, G.vex[w].data);
                visited[w] = 1;
            }
        }
    }
}

int main()
{
    ALGraph G;
    ElemType v[] = "abcdef";
    ElemType a[] = "ab,ac,ad,be,ce,df";
    CreatGraph(G, 6, 6, v, a);
    DFSTraverse(G);
    BFS(G);
    getchar();
    return 0;
}