Andrew BP 神经网络详细推导

Lec 4 BP神经网络详细推导

本篇博客主要记录一下Coursera上Andrew机器学习BP神经网络的前向传播算法和反向传播算法的具体过程及其详细推导。方便后面手撸一个BP神经网络。

目录

• Lec 4 BP神经网络详细推导
  • 4.1 网络结构
    • 4.1.1 损失函数
    • 4.1.2 网络结构
  • 4.2 Forward Propagation
  • 4.3 Back Propagation
    • 4.3.1 第三层权重偏导的求法
    • 4.3.2 第二层权重偏导的求法
    • 4.3.3 第一层权重偏导的求法
    • 4.3.4 直观感受
    • 4.3.5 整合
  • 4.4 整合FP、BP
  • Ref

4.1 网络结构

4.1.1 损失函数

我们选用正规化后的交叉熵函数：

\(J(\Theta) = -\frac{1}{m} \sum\limits_{i=1}^{m} \sum\limits_{k=1}^{K} \left[ {y_k}^{(i)} \log{(h_\Theta(x^{(i)}))}_k + \left( 1 - y_k^{(i)} \right) \log \left( 1- {\left( h_\Theta \left( x^{(i)} \right) \right)} \right)_k \right] + \frac{\lambda}{2m} \sum\limits_{l=1}^{L-1} \sum\limits_{i=1}^{s_l} \sum\limits_{j=1}^{s_{l+1}} \left( \Theta_{ji}^{(l)} \right)^2\)

其中各记号意义如下：

记号	意义
\(m\)	训练集样本个数
\(K\)	分类数目，也即输出层单元个数
\(x^{(i)}\)	训练集的第i个样本输入
\(y^{(i)}\)	训练集的第i个样本输出
\(y_k^{(i)}\)	训练集\(y^{(i)}\)的第k个分量值
\(h_\Theta\)	激活函数，这里是sigmoid函数
\(L\)	网络的层数
\(s_l\)	第 l 层单元的个数

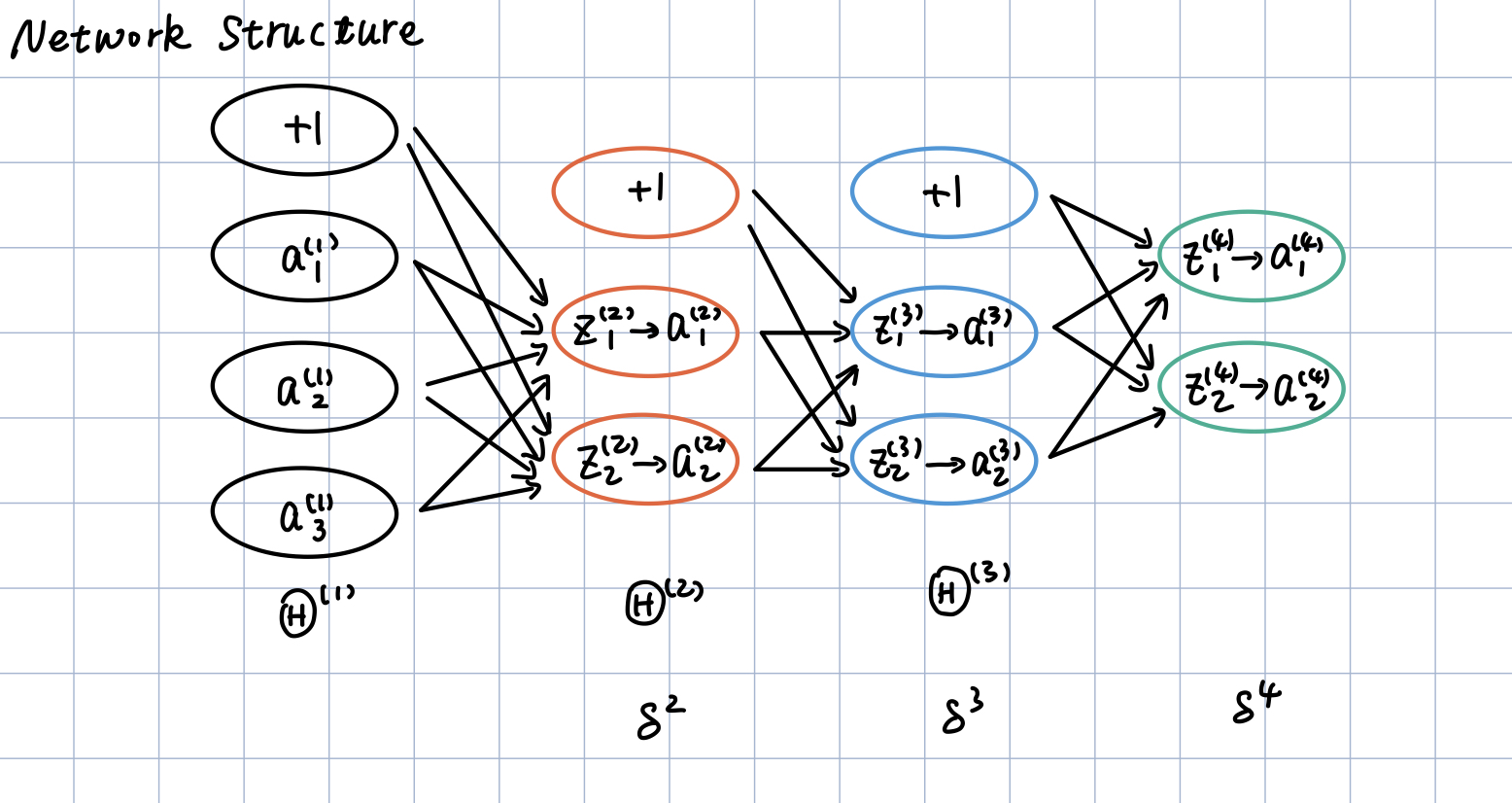
4.1.2 网络结构

同时考虑到推导过程的简洁性和一般性，我们选用如下的网络结构：

即4层神经网络，2个隐含层，输入层4个神经元，输出层2个神经元，两层隐含层每层3个神经元。

4.2 Forward Propagation

从Andrew的网课上我们知道，正向传播算法的大致流程如下图所示：

注意，上图的网络结构不是我们的网络结构。只是懒得写前向传播算法的具体过程从网课上截下来的图。我们的网络结构见上一节。否则后面的推导会比较迷惑

在我们的网络上，大致就对应如下的过程：

第一层的激活值，即我们训练集中的输入：

\[a^{(1)}=\begin{bmatrix}a^{(1)}_0 \\ a^{(1)}_1 \\ a^{(1)}_2\\a^{(1)}_3\end{bmatrix}\tag{1}
\]

第一层的权重，应该为一个2$\times$4的矩阵，如下：

\[\Theta^{(1)}=\begin{bmatrix}\theta^{(1)}_{10} & \theta^{(1)}_{11} & \theta^{(1)}_{12} &\theta^{(1)}_{13} \\
\theta^{(1)}_{20} & \theta^{(1)}_{21} & \theta^{(1)}_{22} & \theta^{(1)}_{23}
\end{bmatrix}\tag{2}
\]

注意，这里的\(\Theta\)矩阵中的元素的角标前一个对应的是下一层的神经元序号，后一个对应的是本层神经元的序号。并且本文中的推导全部遵循这个规定。

对第一层的激活值加权，得到z向量：

\[z^{(2)}=\Theta^{(1)} \times a^{(1)} = \begin{bmatrix}
z^{(2)}_1\\
z^{(2)}_2
\end{bmatrix}\tag{3}
\]

对z向量应用激活函数，其后补充第二层的偏置单元，得到第三层的激活值：

\[g(z^{(2)})=\begin{bmatrix}a^{(2)}_1 \\ a^{(2)}_2\end{bmatrix}\tag{4}\\
\]

\[a^{(2)}=[1; g(z^{(2)})]=\begin{bmatrix}
a^{(2)}_0 \\ a^{(2)}_1 \\ a^{(2)}_2
\end{bmatrix}\tag{5}
\]

其中，这里的激活函数是早期神经网络喜欢使用的sigmoid函数：

\[g(z)=\frac{1}{1+e^{-z}}
\]

其导数具有如下性质：

\[g^{'}(z)=g(z)*(1-g(z))
\]

同理有：

\[\Theta^{(2)}=\begin{bmatrix}\theta^{(2)}_{10} & \theta^{(2)}_{11} & \theta^{(2)}_{12} \\
\theta^{(2)}_{20} & \theta^{(2)}_{21} & \theta^{(2)}_{22}
\end{bmatrix}\tag{6}
\]

\[z^{(3)}=\Theta^{(2)} \times a^{(2)} = \begin{bmatrix}z^{(3)}_1\\z^{(3)}_2\end{bmatrix}\tag{7}
\]

\[a^{(3)}=[1; g(z^{(3)})]=\begin{bmatrix}
a^{(3)}_0 \\ a^{(3)}_1 \\ a^{(3)}_2
\end{bmatrix}\tag{8}
\]

\[\Theta^{(3)}=\begin{bmatrix}\theta^{(3)}_{10} & \theta^{(3)}_{11} & \theta^{(3)}_{12} \\
\theta^{(3)}_{20} & \theta^{(3)}_{21} & \theta^{(3)}_{22}
\end{bmatrix}\tag{9}
\]

快结束了，我们的前向传播算法只剩最后的输出层了：

\[z^{(4)}=\Theta^{(3)} \times a^{(3)} = \begin{bmatrix}z^{(4)}_1\\z^{(4)}_2\end{bmatrix}\tag{10}
\]

注意，已经到输出层了，在这一层不需要添加偏置项：

\[a^{(4)}=h_\Theta(x^{(i)})=g(z^{(4)})=\begin{bmatrix}
a^{(4)}_1\\
a^{(4)}_2
\end{bmatrix}\tag{11}
\]

已经根据我们的训练样本得到了预测值了，接下来就是如何使用梯度下降法更新\(\Theta\)矩阵来使损失函数收敛到一个局部最小值了。这就涉及到了反向传播算法。

4.3 Back Propagation

算法流程：

我们知道反向传播算法是基于梯度下降法的，而梯度下降法的核心在于如何求出损失函数J关于权重矩阵\(\Theta\)的偏导，即梯度。

要理解这一部分的内容，必须要对多元函数的链式求导法则有一个比较好的掌握，具体可以参考3b1b的The Essence of Calculus和Visualizing the chain rule and product rule。

首先，我们可以画出如下的求导链：

在这里，我们先只关注图的上半部分，从求导链中可以看出，如果我们想要减小损失函数的值，有三种办法：

1. 求J关于\(\Theta\)的偏导，使损失函数J沿下降比较快的方向下降，也即调整\(\Theta\)矩阵(weights)
2. 减小上一层的激活值\(a^{(L-1)}\)
3. 减小偏置值（bias)

不知道Andrew的神经网络模型是在严格模仿神经元激活的阈值基本不变还是什么原因，Andrew的每个ML模型都没有调整bias的大小。因此，我们这里也依照课程里的BP神经网络，不调整bias的大小。自然而然地，我们的正规化也不惩罚偏置项。所以，我们就只调整\(\Theta\)矩阵的值以及减小上一层的激活值，而上一层的激活值显然可以层层的向后传播下去。因此，整体来看，我们只用调整权重\(\Theta\)矩阵的值。

因此，接下来的部分我们就看看如何求解损失函数关于\(\Theta\)的偏导。

4.3.1 第三层权重偏导的求法

我们考虑脚标先求解一个损失函数J关于第三层的权重\(\theta_{10}^{(3)}\)的偏导：

先看损失函数：

\(J(\Theta) = -\frac{1}{m} \sum\limits_{i=1}^{m} \sum\limits_{k=1}^{K} \left[ {y_k}^{(i)} \log{(h_\Theta(x^{(i)}))}_k + \left( 1 - y_k^{(i)} \right) \log \left( 1- {\left( h_\Theta \left( x^{(i)} \right) \right)} \right)_k \right] + \frac{\lambda}{2m} \sum\limits_{l=1}^{L-1} \sum\limits_{i=1}^{s_l} \sum\limits_{j=1}^{s_{l+1}} \left( \Theta_{ji}^{(l)} \right)^2\)

简化一下，我们知道正规化这一部分\(\frac{\lambda}{2m} \sum\limits_{l=1}^{L-1} \sum\limits_{i=1}^{s_l} \sum\limits_{j=1}^{s_{l+1}} \left( \Theta_{ji}^{(l)} \right)^2\)的求导比较容易，所以在接下来的求导过程中暂且忽略这一项，放在最后整合的时候再考虑；然后代入第三层的参数，可以得到：

\[\begin{align*}
J(\Theta) &= -\frac{1}{m}\sum_{i=1}^m\sum_{k=1}^K\left[y_k^{(i)}log(a_k^{(4)}) + (1-y_k^{(i)})log(1-a_k^{(4)})\right]\\\\

\frac{\partial J}{\partial a_1^{(4)}} &= -\frac{1}{m}\sum_{i=1}^m\left[y_1^{(i)}\frac{1}{a_1^{(4)}} - (1-y_1^{(i)})\frac{1}{1-a_1^{(4)}}\right]\\\\

\frac{\partial a_1^{(4)}}{\partial z_1^{(4)}} &= \frac{\partial g(z_1^{(4)})}{\partial z_1^{(4)}} \\&= g(z_1^{4})(1-g(z_1^{(4)})) \\
&=a_1^{(4)}(1-a_1^{(4)})\\\\

\frac{\partial z_1^{(4)}}{\partial\theta^{(3)}_{10}} &= a_0^{(3)}
\end{align*}
\]

注意看网络结构图，\(\theta_{10}^{(3)}\)只会影响到\(z_1^{(4)}\)进而影响到\(a_1^{(4)}\)（因此，熟悉多元微分的链式求导法则的朋友应该知道上述向量求导中有一项为0的偏导连乘没有写出来）

根据链式求导图上的求导链，将上述三者相乘：

\[\frac{\partial J}{\partial \theta_{10}^{(3)}} = \frac{1}{m}\sum_{i=1}^m\left[a_1^{(4)} - y_1^{(i)}\right]a_0^{(3)}
\]

同理，我们可以直接写第三层其他所有权重的偏导：

\[\frac{\partial J}{\partial \theta_{11}^{(3)}} = \frac{1}{m}\sum_{i=1}^m\left[a_1^{(4)} - y_1^{(i)}\right]a_1^{(3)}\\\\

\frac{\partial J}{\partial \theta_{12}^{(3)}} = \frac{1}{m}\sum_{i=1}^m\left[a_1^{(4)} - y_1^{(i)}\right]a_2^{(3)}\\\\

\frac{\partial J}{\partial \theta_{20}^{(3)}} = \frac{1}{m}\sum_{i=1}^m\left[a_2^{(4)} - y_2^{(i)}\right]a_0^{(3)}\\\\

\frac{\partial J}{\partial \theta_{21}^{(3)}} = \frac{1}{m}\sum_{i=1}^m\left[a_2^{(4)} - y_2^{(i)}\right]a_1^{(3)}\\\\

\frac{\partial J}{\partial \theta_{22}^{(3)}} = \frac{1}{m}\sum_{i=1}^m\left[a_2^{(4)} - y_2^{(i)}\right]a_2^{(3)}
\]

4.3.2 第二层权重偏导的求法

好像有点规律，接下来我们再求损失函数J关于第二层的权重\(\theta^{(2)}_{10}\)的偏导：

根据网络结构图和求导链可以知道：

\[\begin{align*}

\frac{\partial J}{\partial \theta^{(2)}_{10}}&=\left(\bigg(
\frac{\partial J}{\partial a^{(4)}_1}\cdot\frac{\partial a^{(4)}_1}{\partial z^{(4)}_1}\bigg)\cdot \frac{\partial z^{(4)}_1}{\partial a^{(3)}_1}

+ \bigg(\frac{\partial J}{\partial a^{(4)}_2}\cdot \frac{\partial a^{(4)}_2}{\partial z^{(4)}_2}\bigg)\cdot \frac{\partial z^{(4)}_2}{\partial a^{(3)}_1 }
\right)\cdot \frac{\partial a^{(3)}_1}{\partial z^{(3)}_1} \cdot \frac{\partial z^{(3)}_1}{\partial \theta^{(2)}_{10}}\\

&=\left(
\frac{\partial J}{\partial a^{(4)}_1}\cdot\frac{\partial a^{(4)}_1}{\partial z^{(4)}_1}\cdot \frac{\partial z^{(4)}_1}{\partial a^{(3)}_1}

+ \frac{\partial J}{\partial a^{(4)}_2}\cdot \frac{\partial a^{(4)}_2}{\partial z^{(4)}_2}\cdot \frac{\partial z^{(4)}_2}{\partial a^{(3)}_1 }
\right)\cdot \frac{\partial a^{(3)}_1}{\partial z^{(3)}_1} \cdot \frac{\partial z^{(3)}_1}{\partial \theta^{(2)}_{10}}\\

\end{align*}
\]

仔细看上面的求导链可以发现，实际上在算第二层权重的偏导的时候，有些项（比如\(\frac{\partial J}{\partial a_1^{(4)}}, \frac{\partial a_1^{(4)}}{\partial z_1^{(4)}}\)都已经被计算过了，我们在这里可以直接代入进去。

\[\begin{align*}
\frac{\partial J}{\partial \theta^{(2)}_{10}}&=\left[\frac{1}{m}\sum_{i=1}^m\left[a_1^{(4)} - y_1^{(i)}\right]\cdot \theta_{11}^{(3)}

+ \frac{1}{m}\sum_{i=1}^m\left[a_2^{(4)} - y_2^{(i)}\right] \cdot \theta_{21}^{(3)}
\right] \cdot g^{'}(z_1^{(3)})\cdot a^{(2)}_0\\

&=\frac{1}{m}\sum_{i=1}^m\left[
\left(a_1^{(4)} - y_1^{(i)}\right)\cdot \theta_{11}^{(3)}
+ \left(a_2^{(4)} - y_2^{(i)}\right) \cdot \theta_{21}^{(3)}
\right]\cdot g^{'}(z_1^{(3)})\cdot a^{(2)}_0\\
\end{align*}
\]

类似的，我们可以写出其余几项：

\[\frac{\partial J}{\partial \theta_{11}^{(2)}}=\frac{1}{m}\sum_{i=1}^m\left[
\left(a_1^{(4)} - y_1^{(i)}\right)\cdot \theta_{11}^{(3)}
+ \left(a_2^{(4)} - y_2^{(i)}\right) \cdot \theta_{21}^{(3)}
\right]\cdot g^{'}(z_1^{(3)})\cdot a^{(2)}_1\\
\]

\[\frac{\partial J}{\partial \theta_{12}^{(2)}}=\frac{1}{m}\sum_{i=1}^m\left[
\left(a_1^{(4)} - y_1^{(i)}\right)\cdot \theta_{11}^{(3)}
+ \left(a_2^{(4)} - y_2^{(i)}\right) \cdot \theta_{21}^{(3)}
\right]\cdot g^{'}(z_1^{(3)})\cdot a^{(2)}_2\\
\]

\[\frac{\partial J}{\partial \theta_{20}^{(2)}}=\frac{1}{m}\sum_{i=1}^m\left[
\left(a_1^{(4)} - y_1^{(i)}\right)\cdot \theta_{12}^{(3)}
+ \left(a_2^{(4)} - y_2^{(i)}\right) \cdot \theta_{22}^{(3)}
\right]\cdot g^{'}(z_2^{(3)})\cdot a^{(2)}_0\\
\]

\[\frac{\partial J}{\partial \theta_{21}^{(2)}}=\frac{1}{m}\sum_{i=1}^m\left[
\left(a_1^{(4)} - y_1^{(i)}\right)\cdot \theta_{12}^{(3)}
+ \left(a_2^{(4)} - y_2^{(i)}\right) \cdot \theta_{22}^{(3)}
\right]\cdot g^{'}(z_2^{(3)})\cdot a^{(2)}_1\\
\]

\[\frac{\partial J}{\partial \theta_{20}^{(2)}}=\frac{1}{m}\sum_{i=1}^m\left[
\left(a_1^{(4)} - y_1^{(i)}\right)\cdot \theta_{12}^{(3)}
+ \left(a_2^{(4)} - y_2^{(i)}\right) \cdot \theta_{22}^{(3)}
\right]\cdot g^{'}(z_2^{(3)})\cdot a^{(2)}_2\\
\]

4.3.3 第一层权重偏导的求法

好像规律还不是很明显，那接下来我们求第一层的权重的偏导。

首先，还是可以写出如下的求导链：

\[\begin{align*}

\frac{\partial J}{\partial \theta_{10}^{(1)}} &=
\left[
\left(
\frac{\partial J}{\partial a^{(4)}_1}\cdot\frac{\partial a^{(4)}_1}{\partial z^{(4)}_1}\cdot \frac{\partial z^{(4)}_1}{\partial a^{(3)}_1}
+ \frac{\partial J}{\partial a^{(4)}_2}\cdot \frac{\partial a^{(4)}_2}{\partial z^{(4)}_2}\cdot \frac{\partial z^{(4)}_2}{\partial a^{(3)}_1 }
\right) \cdot \frac{\partial a_1^{(3)}}{\partial z_1^{(3)}} \cdot \frac{\partial z_1^{(3)}}{\partial a_1^{(2)}} \\
+
\left(
\frac{\partial J}{\partial a^{(4)}_1}\cdot\frac{\partial a^{(4)}_1}{\partial z^{(4)}_1}\cdot \frac{\partial z^{(4)}_1}{\partial a^{(3)}_2}
+ \frac{\partial J}{\partial a^{(4)}_2}\cdot \frac{\partial a^{(4)}_2}{\partial z^{(4)}_2}\cdot \frac{\partial z^{(4)}_2}{\partial a^{(3)}_2}
\right)\cdot \frac{\partial a_2^{(3)}}{\partial z_2^{(3)}} \cdot \frac{\partial z_2^{(3)}}{\partial a_1^{(2)}}
\right]\cdot \frac{\partial a_1^{(2)}}{\partial z_1^{(2)}}\cdot \frac{\partial z_1^{(2)}}{\partial \theta_{10}^{(1)}}
\end{align*}
\]

看起来真的是个很复杂的求导公式，但是如果我们自习观察这个式子和第二层的求导链，我们会发现，好像又有很多重复项，比如：

\[\frac{\partial J}{\partial a^{(4)}_1}\cdot\frac{\partial a^{(4)}_1}{\partial z^{(4)}_1}\cdot \frac{\partial z^{(4)}_1}{\partial a^{(3)}_1}

+ \frac{\partial J}{\partial a^{(4)}_2}\cdot \frac{\partial a^{(4)}_2}{\partial z^{(4)}_2}\cdot \frac{\partial z^{(4)}_2}{\partial a^{(3)}_1 }
\]

以及

\[\frac{\partial J}{\partial a^{(4)}_1}\cdot\frac{\partial a^{(4)}_1}{\partial z^{(4)}_1}\cdot \frac{\partial z^{(4)}_1}{\partial a^{(3)}_2}
+ \frac{\partial J}{\partial a^{(4)}_2}\cdot \frac{\partial a^{(4)}_2}{\partial z^{(4)}_2}\cdot \frac{\partial z^{(4)}_2}{\partial a^{(3)}_2}
\]

那又有什么关系呢？不妨再求一下损失函数J关于第一层权重的偏导：

由于第一层的权重矩阵的大小为：\(2\times4\)属实有点多，我们这里只写出\(\frac{\partial J}{\theta_{10}^{(1)}}\)，其余的根据求导链求是类似的：

\[\begin{align*}

\frac{\partial J}{\partial \theta_{10}^{(1)}} &=
\left[
\frac{1}{m}\sum_{i=1}^m\left[
\left(a_1^{(4)} - y_1^{(i)}\right)\cdot \theta_{11}^{(3)}
+ \left(a_2^{(4)} - y_2^{(i)}\right) \cdot \theta_{21}^{(3)}
\right]\cdot g^{'}(z_1^{(3)}) \cdot \theta_{11}^{(2)} \\
+
\frac{1}{m}\sum_{i=1}^m\left[
\left(a_1^{(4)} - y_1^{(i)}\right)\cdot \theta_{12}^{(3)}
+ \left(a_2^{(4)} - y_2^{(i)}\right) \cdot \theta_{22}^{(3)}
\right]\cdot g^{'}(z_2^{(3)})\cdot \theta_{21}^{(2)}
\right]\cdot g^{'}(z_1^{(2)})\cdot a_0^{(1)}\\\\

&=\frac{1}{m}\sum_{i=1}^m
\left[
\left[
\left(a_1^{(4)} - y_1^{(i)}\right)\cdot \theta_{11}^{(3)}
+ \left(a_2^{(4)} - y_2^{(i)}\right) \cdot \theta_{21}^{(3)}
\right]\cdot g^{'}(z_1^{(3)}) \cdot \theta_{11}^{(2)}
\\+
\left[
\left(a_1^{(4)} - y_1^{(i)}\right)\cdot \theta_{12}^{(3)}
+ \left(a_2^{(4)} - y_2^{(i)}\right) \cdot \theta_{22}^{(3)}
\right]\cdot g^{'}(z_2^{(3)})\cdot \theta_{21}^{(2)}
\right]\cdot g^{'}(z_1^{(2)})\cdot a_0^{(1)}

\end{align*}
\]

好像越算越复杂，确实。

不过这个式子有没有一些比较好的性质呢？有！

\[\frac{\partial J}{\partial \theta_{10}^{(1)}} = \frac{1}{m} \sum_{i=1}^m\cdot
\left[
(\Theta^{(2)})^T\times(\Theta^{(3)})T\times(a^{(4)}-y^{(i)}) \quad.* \quad g^{'}(z^{(3)})\quad .* \quad g^{'}(z^{(2)})
\right]_i \cdot a_0^{(1)}
\]

怎么能想到这个式子呢？可以仔细看一看上面的求导结果，就会很想向量化。

4.3.4 直观感受

Neurals fire together if they wire together.

我们不妨把损失函数关于三层的第一个权重的偏导放在一起看看：

\[\begin{align*}

\frac{\partial J}{\partial \theta_{10}^{(3)}} &= \frac{1}{m}\sum_{i=1}^m\left[a_1^{(4)} - y_1^{(i)}\right]a_0^{(3)}\\\\

\frac{\partial J}{\partial \theta^{(2)}_{10}}&=\frac{1}{m}\sum_{i=1}^m\left[
\left(a_1^{(4)} - y_1^{(i)}\right)\cdot \theta_{11}^{(3)}
+ \left(a_2^{(4)} - y_2^{(i)}\right) \cdot \theta_{21}^{(3)}
\right]\cdot g^{'}(z_1^{(3)})\cdot a^{(2)}_0\\\\

\frac{\partial J}{\partial \theta_{10}^{(1)}}&=\frac{1}{m}\sum_{i=1}^m
\left[
\left[
\left(a_1^{(4)} - y_1^{(i)}\right)\cdot \theta_{11}^{(3)}
+ \left(a_2^{(4)} - y_2^{(i)}\right) \cdot \theta_{21}^{(3)}
\right]\cdot g^{'}(z_1^{(3)}) \cdot \theta_{11}^{(2)}
\\+
\left[
\left(a_1^{(4)} - y_1^{(i)}\right)\cdot \theta_{12}^{(3)}
+ \left(a_2^{(4)} - y_2^{(i)}\right) \cdot \theta_{22}^{(3)}
\right]\cdot g^{'}(z_2^{(3)})\cdot \theta_{21}^{(2)}
\right]\cdot g^{'}(z_1^{(2)})\cdot a_0^{(1)}
\end{align*}
\]

好像有些东西在一次又一次的被计算，看不出来规律没问题，我们再看看我们的求导链：

在这里我们只关注图的下半部分，我们会发现：

\[\begin{align*}

\frac{\partial J}{\partial z^{(4)}} &= a^{(4)}-y^{(i)}, we\quad denoted \quad this \quad term \quad by \quad \delta^{(4)}\\\\

\frac{\partial J}{\partial z^{(3)}} &= \delta^{(3)}=(\Theta^{(3)})^T\delta^{(4)} \quad .* \quad g^{'}(z^{(3)})\\\\

\frac{\partial J}{\partial z^{(2)}} &= \delta^{(2)}=(\Theta^{(2)})^T\delta^{(3)} \quad .* \quad g^{'}(z^{(2)})
\end{align*}
\]

分别对应上图下半部分红色线，绿色线，蓝色线划出的内容，也就是：

同时也能理解：

然后，再看

\[\frac{\partial J}{\partial \theta_{10}^{(1)}} = \frac{1}{m} \sum_{i=1}^m\cdot
\left[
(\Theta^{(2)})^T\times(\Theta^{(3)})T\times(a^{(4)}-y^{(i)}) \quad.* \quad g^{'}(z^{(3)})\quad .* \quad g^{'}(z^{(2)})
\right]_i \cdot a_0^{(1)}
\]

会发觉：

\[\frac{\partial J}{\partial \theta_{10}^{(1)}} = \frac{1}{m} \sum_{i=1}^m\cdot \delta^{(2)}_1 \cdot a_0^{(1)}
\]

显然，其余的所有权重的偏导都可以写成这么一个很简洁明了的式子。okay，推导过程虽然很繁杂但结果还是挺漂亮的。

我们再回想一下，\(\delta^{(4)}\)说明了我们\(\Theta\)的调整和我们预测值与实际值之间的距离有关，而反向传播的过程其实正好体现在了\(\delta^{(4)}, \delta^{(3)}, \delta^{(2)}\)的求法上，我们调整\(\Theta\)的值，使得几个\(\delta\)逐渐减小。

4.3.5 整合

别忘了，我们还有正规化项没有考虑。考虑正规化项，整合之后：

\[\begin{equation}

\frac{\partial}{\partial \Theta^{(l)}_{ij}}J(\Theta) =
\begin{cases}
\frac{1}{m}\Delta^{(l)}_{ij}+\lambda\Theta^{(l)}_{ij}& if\quad j \ne 0, \\\\
\frac{1}{m}\Delta^{(l)}_{ij}&if\quad j=0
\end{cases}, \\\\

\text{where } \Delta^{(l)}_{ij}=\sum_{i=1}^ma_j^{(l)}*\delta^{(l+1)}
\end{equation}
\]

4.4 整合FP、BP

刚学完BP神经网络：神经网络就这？

看完BP算法：啥啥啥？这都啥

推完BP算法：什么嘛？整个BP算法就链式求导法则啊

其实仔细想想，神经网络好像也就一个多元函数的优化问题，不过上世纪受限于计算能力，没有兴盛起来。而随着计算能力的发展，我们存储链式求导中的每一条边的值，使得反向传播的过程成为了可能。也就是为什么神经网络在如今流行起来了。

Ref

1 吴恩达机器学习

2 3b1b 深度学习