机器学习-----线性回归浅谈（Linear Regression）

Linear Regreesion  

       在现实生活中普遍存在着变量之间的关系，有确定的和非确定的。确定关系指的是变量之间可以使用函数关系式表示，还有一种是属于非确定的（相关），比如人的身高和体重，一样的身高体重是不一样的。

      线性回归：

           1： 函数模型（Model）：

                 

           假设有训练数据

                

          那么为了方便我们写成矩阵的形式

                

         2： 损失函数（cost）：

                 现在我们需要根据给定的X求解W的值，这里采用最小二乘法。   

     a.最小二乘法：

      何为最小二乘法，其实很简单。我们有很多的给定点，这时候我们需要找出一条线去拟合它，那么我先假设这个线的方程，然后把数据点代入假设的方程得到观测值，求使得实际值与观测值相减的平方和最小的参数。对变量求偏导联立便可求。

因此损失代价函数为：

3： 算法（algorithm）：

             现在我们的目的就是求解出一个使得代价函数最小的W：

            a.矩阵满秩可求解时（求导等于0）：

                        

  b.矩阵不满秩时（梯度下降）：

梯度下降算法是一种求局部最优解的方法，对于F(x)，在a点的梯度是F(x)增长最快的方向，那么它的相反方向则是该点下降最快的方向，具体参考wikipedia。

原理：将函数比作一座山，我们站在某个山坡上，往四周看，从哪个方向向下走一小步，能够下降的最快；

注意：当变量之间大小相差很大时，应该先将他们做处理，使得他们的值在同一个范围，这样比较准确。

1）首先对θ赋值，这个值可以是随机的，也可以让θ是一个全零的向量。

2）改变θ的值，使得J(θ)按梯度下降的方向进行减少。

描述一下梯度减少的过程，对于我们的函数J(θ)求偏导J：

Repeat  until convergence：{

下面是更新的过程，也就是θi会向着梯度最小的方向进行减少。θi表示更新之前的值，-后面的部分表示按梯度方向减少的量，α表示步长，也就是每次按照梯度减少的方向变化多少。

}

假设有数据集D时：

对损失函数求偏导如下：

使用矩阵表示（方便计算）

    从概率层面解释-回归模型的目标函数：

          基本上每个模型都会有一个对应的目标函数，可以通过不同的最优化求解方法（梯度下降，牛顿法等等）对这些对应的目标函数进行求解。线性回归模型，我们知道实际上是通过多个自变量对自变量进行曲线拟合。我们希望找到一条可以较好拟合的曲线，

那我们如何判断一条曲线的拟合程度的好坏。上面讲到，我们采用的是最小二乘法（预测值和真实值得误差的平方和），那为什么要用这个作为目标函数呢？

可以从中心极限定理、高斯分布来分析：

   1.中心极限定理：

设有n个随机变量，X_1,X₂,X3,Xn,他们之间相互独立，并且有相同的数学期望和均值。E(X)=u;D(x)=δ².令Y_n为这n个随机变量之和。

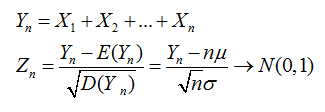
Z_n为X这几个变量的规范和。

       2.高斯分布

假的给定一个输入样本x，我们得到预测值和真实值间的存在的误差e，那么他们的关系如下：

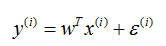
而这里，我们就可以假设e服从标准的高斯分布。

为什么呢？回归模型的最终目标是建立自变量x和y之间的关系，我们希望通过x可以较为准确的表示结果y。而在实际应用场景中，很难甚至不可能把导致y结果的所有变量（特征）都找到，放到回归模型里面。

我们只存放那些认为比较重要的特征。根据中心极限定理，把那些对结果影响比较小的(假设独立分布)之和认为是符合正态分布是合理的。

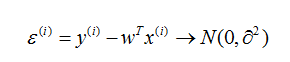
那么x和y的条件概率：

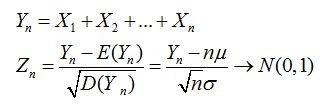
那么知道一条样本的概率，我们就可以通过极大估计求似然函数，优化的目标函数如下：

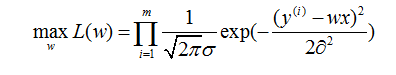
　 通过取对数我们可以发现极大似然估计的目标函数和最小平方误差是一样。

在概率模型中，目标函数的极大和极小与极大似然估计是等价的。

　　　

假设随机变量为Y，和普通变量x存在相关关系，由于Y是随机变量，对于x的各个确定值，Y有它的分布（高斯）。

      假设为:

         

     使用极大似然估计可求解。

     我们知道对于下面公式：

         

      y为随机变量，在c=E(y)时达到最小，这表明以E(y)作为y的近似是最好的。