UVa 1643 Angle and Squares

题意：

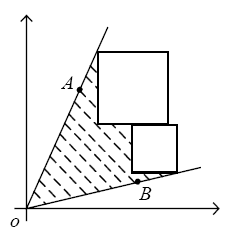
如图，有n个正方形和一个角(均在第一象限中)，使这些正方形与这个角构成封闭的阴影区域，求阴影区域面积的最大值。

分析：

直观上来看，当这n个正方形的对角线在一条直线上时，封闭区域的面积最大。(虽然我不太会证明，=_=||)

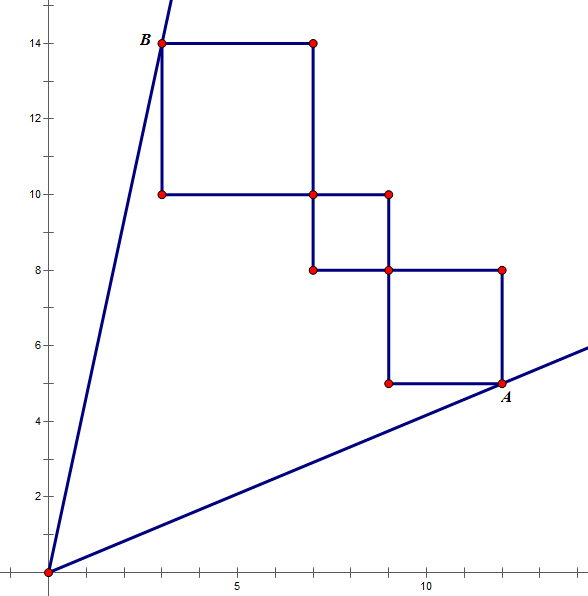
设所有正方形边长之和为L，OA、OB两直线方程分别为：y = k₁x  y = k₂x，设A(x₁, k₁x₁), B(x₂, k₂x₂)，可列出方程：

，解得，相应的就得到AB两点坐标，用叉积算出△OAB的面积再减去这些正方形面积的一半就是答案。

 #include <cstdio>
 #include <algorithm>

 struct Point
 {
     double x, y;
     Point(double x=, double y=):x(x), y(y) {}
 };

 double Cross(const Point& A, const Point& B)
 { return A.x*B.y - A.y*B.x; }

 int main()
 {
     //freopen("in.txt", "r", stdin);
     int n;
     while(scanf("%d", &n) ==  && n)
     {
         Point A, B;
         double L = , subArea = , l;
         scanf("%lf%lf%lf%lf", &A.x, &A.y, &B.x, &B.y);
         for(int i = ; i < n; ++i)
         {
             scanf("%lf", &l);
             L += l;
             subArea += l * l / ;
         }
         double k1 = A.y / A.x, k2 = B.y / B.x;
         if(k1 > k2) std::swap(k1, k2);
         double x1 = (k1+)*L/(k2-k1), y1 = k1 * x1;
         double x2 = (k2+)*L/(k2-k1), y2 = k2 * x2;
         A = Point(x1, y1), B = Point(x2, y2);
         double ans = Cross(A, B) /  - subArea;

         printf("%.3f\n", ans);
     }

     return ;
 }

代码君