Differential Geometry之第三章曲面的局部理论

第三章、曲面的局部理论

1.曲面的概念

1.1.曲面的概念

1.2.切平面与法向

2.曲面的第一基本形式

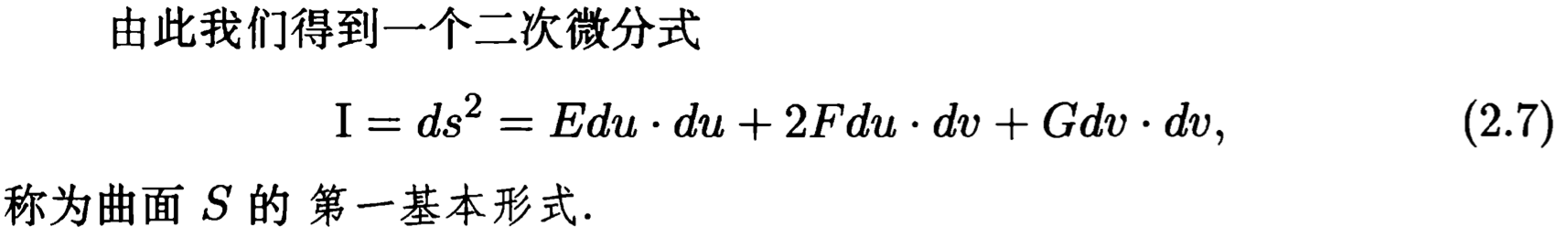
3.曲面的第二基本形式

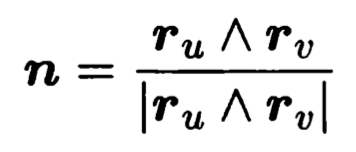
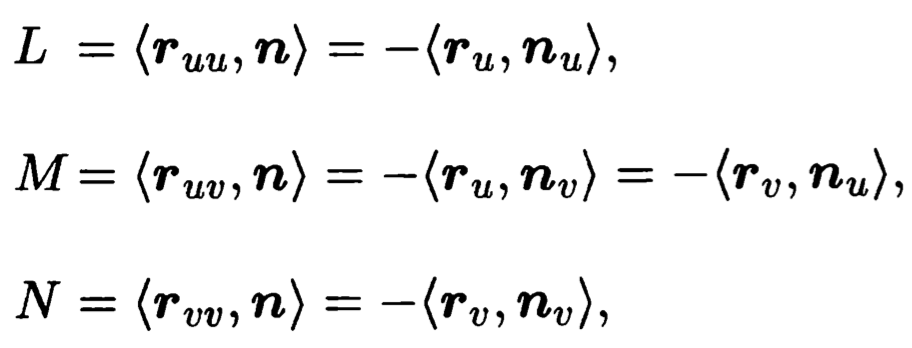
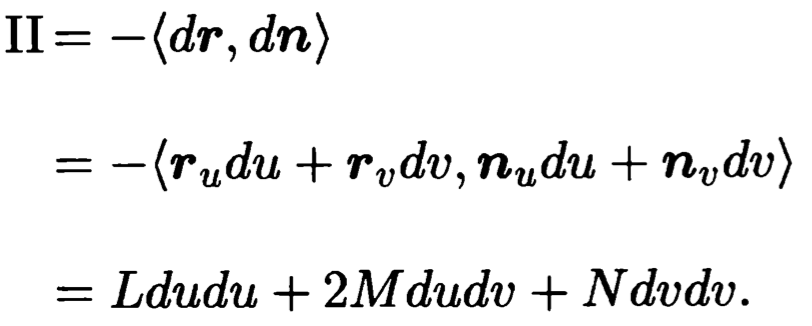
正定矩阵：一个n阶的实对称矩阵M是正定的的条件是当且仅当对于所有的非零实系数向量z，都有zTMz> 0。其中zT表示z的转置。

正定矩阵在合同变换下可化为标准型， 即对角矩阵。

所有特征值大于零的对称矩阵（或厄米矩阵）也是正定矩阵。

判定定理1：对称阵A为正定的充分必要条件是：A的特征值全为正。

判定定理2：对称阵A为正定的充分必要条件是：A的各阶顺序主子式都为正。

判定定理3：任意阵A为正定的充分必要条件是：A合同于单位阵。

正定矩阵的性质：

1.正定矩阵的任一主子矩阵也是正定矩阵。

2.若A为n阶对称正定矩阵，则存在唯一的主对角线元素都是正数的下三角阵L，使得A=L*L′，此分解式称为 正定矩阵的乔列斯基（Cholesky）分解。

3.若A为n阶正定矩阵，则A为n阶可逆矩阵。

4.正定矩阵对角线元素都大于零。证明：取基向量，由定义可知其对角线元素均大于零。

负定矩阵：设A是实对称矩阵。如果对任意的实非零列矩阵X有XTAX<0，就称A为负定矩阵。

它在合同相似变换下，可以变成(-E), 这里 E 是单位矩阵。

1. A是负定矩阵的充要条件是：-A是正定矩阵。

2. A是负定矩阵的充要条件是：A^{-1}是负定矩阵。

3. A是负定矩阵的充要条件是：A的所有奇数阶顺序主子式小于零，所有偶数阶顺序主子式大于零。

4.负定矩阵对角线元素都小于零。证明：取基向量，由定义可知其对角线元素均小于零。

不定矩阵：若A∈Mn（K）是不定矩阵的充要条件是：存在列向量组X，Y，使得XTAX>0，YTAY<0。

若实对称矩阵A的主对角线上元素有正有负，则A一定是不定矩阵。

4.法曲率与Weingarten变换

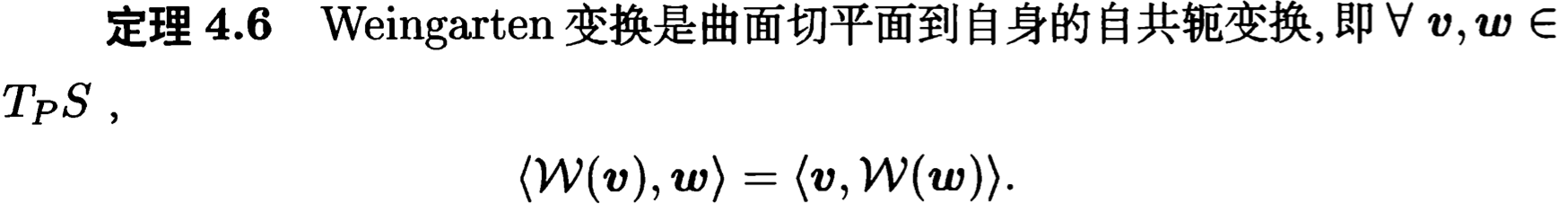
5.主曲率与Gauss曲率

6.曲面的一些例子

6.1.旋转曲面

6.1.1.常Gauss曲率旋转曲面

6.1.2.常平均曲率旋转曲面

6.2.直纹面与可展曲面

6.3.全脐点曲面