OPENGL 坐标轴转换
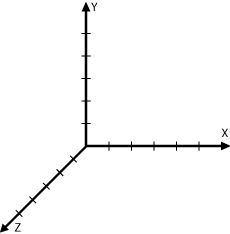
- 坐标轴
- 平移
- 旋转
- 缩放
- 重置坐标轴
- 矩阵操作
- 示例
public abstract void glTranslatef(float x ,float y, float z)
gl.glTranslatef(0,0,-3);
3、旋转
public abstract void glRotatef(float angle,float x,float y,float z)
public abstract void glScalef(float x,float y,float z)
gl.glTranslatef(2,0,0);
gl.glScalef(0.5f,0.5f,0.5f);
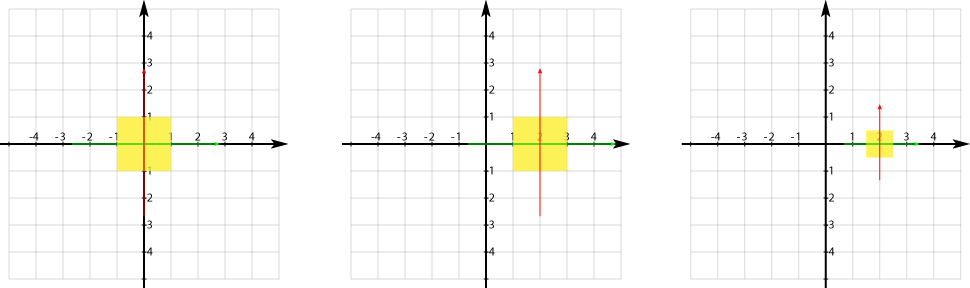
先进行缩放,后平移
gl.glScanlef(0.5f,0.5f,0.5f);
gl.glTranslatef(2,0,0);

public abstract void glLoadIdentity();
public abstract void glPushMatrix();
复制当前操作后的矩阵保存到堆栈中.
glPopMatrix
public abstract void glPopMatrix();
public class GLES20Renderer3 implements GLSurfaceView.Renderer{
private Square square;
private float angle=0;
public GLES20Renderer3(){
square=new Square();
}
@Override
public void onSurfaceCreated(GL10 gl, EGLConfig config) {
gl.glClearColor(0.0f,0.0f,0.0f,0.5f);
gl.glShadeModel(GL10.GL_SMOOTH);
gl.glClearDepthf(1.0f);
gl.glEnable(GL10.GL_DEPTH_TEST);
gl.glDepthFunc(GL10.GL_LEQUAL);
gl.glHint(GL10.GL_PERSPECTIVE_CORRECTION_HINT,GL10.GL_NICEST);
}
@Override
public void onSurfaceChanged(GL10 gl, int width, int height) {
gl.glViewport(0,0,width,height);
gl.glMatrixMode(GL10.GL_PROJECTION);
gl.glLoadIdentity();
GLU.gluPerspective(gl,45.0f,(float)width/(float)height,0.1f,100.0f);
gl.glMatrixMode(GL10.GL_MODELVIEW);
gl.glLoadIdentity();
}
@Override
public void onDrawFrame(GL10 gl) {
gl.glClear(GL10.GL_COLOR_BUFFER_BIT|GL10.GL_DEPTH_BUFFER_BIT);
gl.glLoadIdentity();
gl.glTranslatef(0,0,-10);
//A
gl.glPushMatrix();
gl.glRotatef(angle,0,0,1);
square.draw(gl);
gl.glPopMatrix();
//B
gl.glPushMatrix();
gl.glRotatef(-angle,0,0,1);
gl.glTranslatef(2,0,0);
gl.glScalef(.5f,.5f,.5f);
square.draw(gl);
//C
gl.glPushMatrix();
gl.glRotatef(-angle,0,0,1);
gl.glTranslatef(2,0,0);
gl.glScalef(.5f,.5f,.5f);
square.draw(gl);
gl.glPopMatrix();
gl.glPopMatrix();
angle++;
}
}
public class Square {
private float vertices[]={
-1.0f,1.0f,0.0f,
-1.0f,-1.0f,0.0f,
1.0f,-1.0f,0.0f,
1.0f,1.0f,0.0f,
};
private short[] indices={0,1,2,0,2,3};
private FloatBuffer vertexBuffer;
private ShortBuffer indexBuffer;
public Square(){
ByteBuffer vbb=ByteBuffer.allocateDirect(vertices.length*4);
vbb.order(ByteOrder.nativeOrder());
vertexBuffer=vbb.asFloatBuffer();
vertexBuffer.put(vertices);
vertexBuffer.position(0);
ByteBuffer ibb=ByteBuffer.allocateDirect(indices.length*2);
ibb.order(ByteOrder.nativeOrder());
indexBuffer=ibb.asShortBuffer();
indexBuffer.put(indices);
indexBuffer.position(0);
}
public void draw(GL10 gl){
gl.glFrontFace(GL10.GL_CCW);
gl.glEnable(GL10.GL_CULL_FACE);
gl.glCullFace(GL10.GL_BACK);
gl.glEnableClientState(GL10.GL_VERTEX_ARRAY);
gl.glVertexPointer(3,GL10.GL_FLOAT,0, vertexBuffer);
gl.glDrawElements(GL10.GL_TRIANGLES,indices.length,GL10.GL_UNSIGNED_SHORT,indexBuffer);
gl.glDisableClientState(GL10.GL_VERTEX_ARRAY);
gl.glDisable(GL10.GL_CULL_FACE);
}
}
OPENGL 坐标轴转换的更多相关文章
- cocos2d-x 屏幕坐标系和OPenGL坐标系转换
转自:http://home.cnblogs.com/group/topic/57609.html cocos2d坐标系(OPenGL坐标系):以左下角为原点,x向右,y向上 屏幕坐标系(androi ...
- Codeforces 989 P循环节01构造 ABCD连通块构造 思维对云遮月参考系坐标轴转换
A 直接判存不存在连续的三个包含A,B,C就行 /*Huyyt*/ #include<bits/stdc++.h> #define mem(a,b) memset(a,b,sizeof(a ...
- 3DMAX导出到Unity坐标轴转换问题
这是我在3dmax中创建的1cm*1cm*1cm的立方体,右图为3dmax中的坐标系 当我们把这个立方体导入到unity中发现x轴意外的扭转了90度 为了解决这个问题,你需要对模型做出修正 1.选 ...
- obj2opengl:转换OBJ 3D模型到iPhone OpenGL ES兼容的数组中
原文如下:obj2opengl: convert obj 3D models to arrays compatible with iPhone OpenGL ES obj2opengl在GitHub中 ...
- iOS——Core Animation 知识摘抄(四)
原文地址http://www.cocoachina.com/ios/20150106/10840.html 延迟解压 一旦图片文件被加载就必须要进行解码,解码过程是一个相当复杂的任务,需要消耗非常长的 ...
- OSG模型简单控制
OSG模型简单控制 转自:http://milkcu.sintune.net/blog/archives/1392673560.html 结点基本操作 添加结点 OSG中使用osg::Node和osg ...
- [OSG]如何用Shader得到物体的世界坐标
来自:http://www.cnblogs.com/hesicong/archive/2008/05/27/1208312.html 最近群里面有个朋友问我关于如何得到OpenGL世界坐标的问题,当时 ...
- CoreAnimation6-基于定时器的动画和性能调优
基于定时器的动画 定时帧 动画看起来是用来显示一段连续的运动过程,但实际上当在固定位置上展示像素的时候并不能做到这一点.一般来说这种显示都无法做到连续的移动,能做的仅仅是足够快地展示一系列静态图片,只 ...
- 【转】iOS-Core-Animation-Advanced-Techniques(六)
原文:http://www.cocoachina.com/ios/20150106/10839.html 基于定时器的动画和性能调优 基于定时器的动画 我可以指导你,但是你必须按照我说的做. -- 骇 ...
随机推荐
- 添加-ObjC的含义
http://www.cnblogs.com/yashi88/p/3551947.html 参考文章 当使用某个第三方库时,遇到 出现"selector not recognized&quo ...
- border-radius:50%和100%的区别
border-radius 值类型-百分比 border-radius的值是百分比的话,就相当于盒子的宽度和高度的百分比. 我们知道在一个正方形内做一个面积最大的圆形,这个圆的半径就为正方形边长的一半 ...
- 2018HDU多校二 -F 题 Naive Operations(线段树)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=6315 In a galaxy far, far away, there are two integer ...
- 教你们学习一个最简单又企业最需要的服务-crond
第13章 定时任务的介绍 13.1 定时任务的分类 13.1.1 系统实现定时任务的配置 [root@oldboyedu ~] # cd /etc/cron. cron.d/ cron.daily/ ...
- Nios II的Boot过程分析
目录 1 概述....................................................................... 1 2 几种常见的 ...
- jqurey(尺寸,css操作,效果,遍历)
尺寸: height():设置或返回元素的高度(不包括内边距.边框或外边距). width():设置或返回元素的宽度(不包括内边距.边框或外边距). 例如: $("#box").h ...
- Eclipse Properties编辑
1.使用Eclipse插件编辑,这是本人推荐的方式 UPDATE地址:http://propedit.sourceforge.jp/eclipse/updates 2.使用JDK自带的工具native ...
- Python操作redis和mongoDB
一.操作redis redis是一个key-value存储系统,value的类型包括string(字符串),list(链表),set(集合),zset(有序集合),hash(哈希类型).为了保证效率, ...
- 分享一下HttpWatch pro 10.X 支持win10
今天开始学Servlet,第一次安的是10的普通版,但发现功能太过简单不够学习使用,之后换了9的pro版本,发现单击"Record"按钮启动网络监听,会收到"ERROR_ ...
- 十年Java程序员-带你走进Java虚拟机-类加载机制
类的生命周期 1.加载 将.class文件从磁盘读到内存 2.连接 2.1 验证 验证字节码文件的正确性 2.2 准备 给类的静态变量分配内存,并赋予默认值 2.3 解析 类装载器装入类所引用的其它所 ...
