USACO环绕岛屿Surround the Islands 并查集枚举暴力

题目描述

Farmer John has bought property in the Caribbean and is going to try to raise dairy cows on a big farm composed of islands. Set in his ways, he wants to surround all the islands with fence.

Each island in the farm has the shape of a polygon. He fences the islands one side at a time (between a consecutive pair of vertices) and proceeds clockwise around a given island with his fencing

operations. Since he wants to fence all the islands, he must at some point travel to any other islands using a boat.

He can start fencing at any vertex and, at any vertex he encounters, travel to some vertex on another island, fence all the way around it, and then IMMEDIATELY return back to the same vertex on the original island using the same path he traveled before. Each boat trip has a cost defined by a supplied matrix.

The islands are described by a set of N (3 <= N <= 500) pairs of vertices V1,V2 (1 <= V1 <= N; 1 <= V2 <= N) although you must figure out how to assemble them into islands. The vertices are conveniently numbered 1..N.

The cost of traveling by boat between each pair of vertices is given by a symmetric cost matrix whose elements fall in the range 0..1000.

What is the minimum cost of surrounding the islands with the fence?

约翰在加勒比海买下地产，准备在这里的若干个岛屿上养奶牛．所以，他要给所有岛屿围上篱笆．每个岛屿都是多边形．他沿着岛屿的一条边界朝一个方向走，有时候坐船到另一个岛去．他可以从任意一个多边形顶点开始修篱笆的工作；在任意一个到达的顶点，他可以坐船去另一个岛屿的某个顶点，但修完那个岛的篱笆，他必须马上原路返回这个出发的岛屿顶点．任意两个顶点间都有航线，每条航线都需要一定的费用．请帮约翰计算最少的费用，让他修完所有篱笆．

输入输出格式

输入格式：

* Line 1: A single integer: N

* Lines 2..N+1: Each line describes an island's border with two space-separated integers: V1 and V2

* Lines N+2..2*N+1: Line i-N-1 contains N integers that describe row i of the cost matrix: Row_i

输出格式：

* Line 1: A single integer that specifies the minimum cost of building the fence

输入输出样例

输入样例#1：

12

1 7

7 3

3 6

6 10

10 1

2 12

2 9

8 9

8 12

11 5

5 4

11 4

0 15 9 20 25 8 10 13 17 8 8 7

15 0 12 12 10 10 8 15 15 8 8 9

9 12 0 25 20 18 16 14 13 7 12 12

20 12 25 0 8 13 14 15 15 10 10 10

25 10 20 8 0 16 20 18 17 18 9 11

8 10 18 13 16 0 10 9 11 10 8 12

10 8 16 14 20 10 0 18 20 6 16 15

13 15 14 15 18 9 18 0 5 12 12 13

17 15 13 15 17 11 20 5 0 22 8 10

8 8 7 10 18 10 6 12 22 0 11 12

8 8 12 10 9 8 16 12 8 11 0 9

7 9 12 10 11 12 15 13 10 12 9 0

输出样例#1：

30 

提交地址 ： Luogu2941， Bzoj3397； (然而并没有bzoj权限，桑心）

样例解析 ： 一看样例就不想做系列；并没有好好看样例；
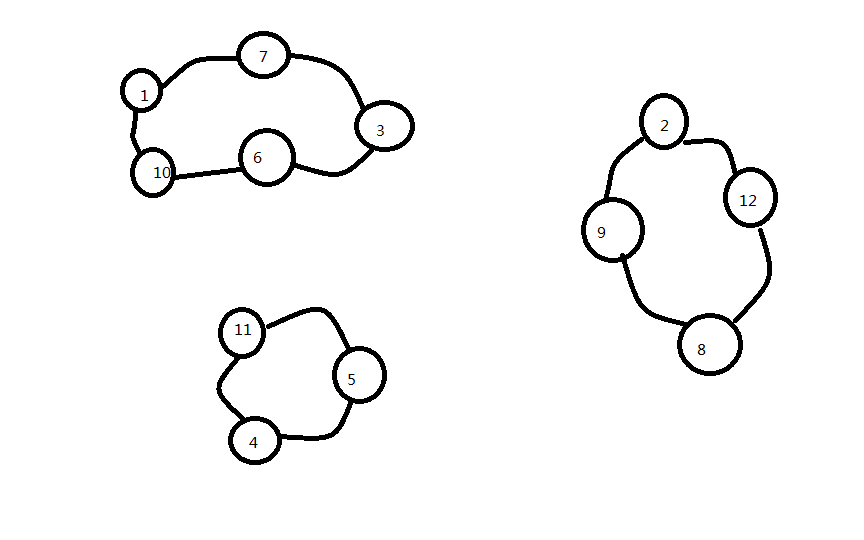
大致看了一下分的岛屿

大概是这个样子的，然后每个点之间都有一些连线表示之间是通路，每条路都有一个权值；

分析 ：
其实仔细想想，既然在每个岛屿中行走不算进总花费，那么可以进行一波缩点，我是用并查集维护，直接求出每个联通块；
这样，我们就把一堆点，抽象成了一堆互不联通的块；
这时再加边权，在每一个联通块内，任何 一个点向外的连线都可看做是这个联通块向外连的线， 这样， 我们把每一个联通块向外的边的权值最小记录下来，当做这个联通块向外的边；
所以，我们只要枚举从哪一个联通块开始出发，把这个联通块与其他联通块的边权和加起来取min再乘2就是答案；

代码奉上：

#include <iostream>

#include <algorithm>

#include <cstdio>

#include <cmath>

#include <cstring>

using namespace std;

#define regi register 

int n;

int fa[];

inline int Find(int x)

{

    return x == fa[x] ? x : fa[x] = Find(fa[x]);

}

int dis[][];

int cnt;

int ans = 0x7f7f7f7f;

int pos[];

int main()

{

    cin >> n;

    for (regi int i =  ; i <= n ; i ++) fa[i] = i;

    memset(dis, 0x7f, sizeof dis);

    for (regi int i =  ; i <= n ; i ++){

        int x, y;

        scanf("%d%d", &x, &y);

        int fx = Find(x), fy = Find(y);

        if (fx != fy) fa[fx] = fy;

    }

    for (regi int i =  ; i <= n ; i ++){

        if (fa[i] == i) pos[++cnt] = i;

    }

    for (regi int i =  ; i <= n ; i ++){

        int fi = Find(i);

        for (regi int j =  ; j <= n ; j ++){

            int fj = Find(j);

            int d;

            scanf("%d", &d);

            dis[fi][fj] = min(dis[fi][fj], d);

        }

    }

    for (regi int i =  ; i <= cnt ; i ++){

        int sum = ;

        for (regi int j =  ; j <= cnt ; j ++){

            if (i == j) continue;

            sum += dis[pos[i]][pos[j]];

        }

        ans = min(ans, sum);

    }

//    printf("dis==%d\n", dis[4][10]);

    cout << ans *  << endl;

    return ;

}

zZhBr

可以转载但请注明出处，谢！