隐马尔科夫模型HMM介绍

马尔科夫链是描述状态转换的随机过程，该过程具备“无记忆”的性质：即当前时刻$t$的状态$s_t$的概率分布只由前一时刻$t-1$的状态$s_{t-1}$决定，与时间序列中$t-1$时刻之前的状态无关。定义马尔科夫链的转移矩阵为$A$，有$$A_{ij}=p\left(s_{t}=j | s_{t-1}=i\right),\text{ }s_{t} | s_{t-1} \sim \operatorname{Discrete}\left(A_{s_{t-1}, :}\right)$$容易看出矩阵$A$的每行之和为1，给定一个起始状态$s_1$(也可通过某个分布产生)，可通过从上述分布中抽样生成序列$\left(s_{1}, s_2, \dots, s_{t}\right)$。

模型定义

隐马尔科夫模型HMM假设观测是从一个隐藏的马尔科夫状态序列生成的，如下图所示：

不失一般性，假设共有$S$个离散状态，即$s \in \{1,2,\dots,S\}$
不失一般性，假设共有$X$种观测，即$x \in \{1,2,\dots,X\}$
定义初始的状态分布为$\vec{\pi}=(\pi_1,\pi_2,\dots,\pi_S)$，即$s_{1} \sim \operatorname{Discrete}(\vec{\pi})$
定义状态$s$的转移矩阵为$\mathcal{A}$，则$\mathcal{A}$为$S$行$S$列的矩阵，即$s_{i} |\left\{s_{i-1}=k^{\prime}\right\} \sim \operatorname{Discrete}\left(\mathcal{A}_{k^{\prime}, :}\right)$
定义观测$x$的生成概率为$\mathcal{B}$，则$\mathcal{B}$为$S$行$X$列的矩阵，即$x_{i} |\left\{s_{i}=k^{\prime}\right\} \sim \operatorname{Discrete}\left(\mathcal{B}_{k^{\prime}, :}\right)$

则HMM的求解可归纳为以下两个问题：

训练：已知观测序列$\vec{o}=(x_1,x_2,\dots,x_T)$，使用最大似然估计计算参数$\vec{\pi},\mathcal{A},\mathcal{B}$，即$$\vec{\pi}_{\mathrm{ML}}, \mathcal{A}_{\mathrm{ML}}, \mathcal{B}_{\mathrm{ML}}=\arg \max _{\vec{\pi},\mathcal{A},\mathcal{B}} p\left(\vec{o} | \vec{\pi},\mathcal{A},\mathcal{B}\right)$$
预测：已知观测序列$\vec{o}$以及参数$\vec{\pi},\mathcal{A},\mathcal{B}$，估计生成观测序列$\vec{o}$的最可能的隐藏状态序列$\vec{s}=(s_{1}, \ldots, s_{T})$，即$$s_{1}, \ldots, s_{T}=\arg \max _{\vec{s}} p\left(\vec{s} | \vec{o}, \vec{\pi},\mathcal{A},\mathcal{B}\right)$$

参数估计

要解决问题1，首先看一下如何估计$p\left(\vec{o} | \vec{\pi},\mathcal{A},\mathcal{B}\right)$，根据概率公式，有$$\begin{aligned} p(\vec{o} | \vec{\pi}, \mathcal{A}, \mathcal{B}) &=\sum_{s_{1}=1}^{S} \cdots \sum_{s_{T}=1}^{S} p\left(\vec{o}, s_{1}, \ldots, s_{T} | \vec{\pi}, \mathcal{A},\mathcal{B}\right) \\ &=\sum_{s_{1}=1}^{S} \cdots \sum_{s_{T}=1}^{S} \pi_{s_1}\mathcal{B}_{s_1,x_1}\prod_{i=2}^{T}\mathcal{A}_{s_{i-1},s_i}\mathcal{B}_{s_i,x_i} \end{aligned}$$如果按上述公式直接进行计算，复杂度为$\mathcal{O}(TS^T)$，效率太低，考虑使用动态规划的思想，将算法复杂度降为$\mathcal{O}(TS^2)$，可以使用两种方式：

1. Forward Algorithm

定义$\alpha_{t}(j)=p\left(x_{1}, x_{2} \ldots x_{t}, s_{t}=j | \vec{\pi}, \mathcal{A},\mathcal{B}\right),\text{ }t\in\{1,2,\cdots,T\},\text{ }j\in\{1,2,\cdots,S\}$，则算法可以写为：
- Initialization: $\alpha_{1}(j)=\pi_j\mathcal{B}_{j,x_1}; \quad 1 \leq j \leq S$
- Recursion: $\alpha_{t}(j)=\sum_{i=1}^{S} \alpha_{t-1}(i) \mathcal{A}_{i j} \mathcal{B}_{j,x_t} ; \quad 1 \leq j \leq S, 1<t \leq T$
- Termination: $p\left(\vec{o} | \vec{\pi},\mathcal{A},\mathcal{B}\right)=\sum_{i=1}^{S} \alpha_{T}(i)$

2. Backward Algorithm

定义$\beta_{t}(i)=p\left(x_{t+1}, x_{t+2} \ldots x_{T} | s_{t}=i, \vec{\pi}, \mathcal{A},\mathcal{B}\right),\text{ }t\in\{1,2,\cdots,T\},\text{ }i\in\{1,2,\cdots,S\}$，则算法可以写为：
- Initialization: $\beta_{T}(i)=1; \quad 1 \leq i \leq S$
- Recursion: $\beta_{t}(i)=\sum_{j=1}^{S} \mathcal{A}_{i j} \mathcal{B}_{j,x_{t+1}} \beta_{t+1}(j) ; \quad 1 \leq i \leq S, 1 \leq t < T$
- Termination: $p\left(\vec{o} | \vec{\pi},\mathcal{A},\mathcal{B}\right)=\sum_{j=1}^{S} \pi_{j} \mathcal{B}_{j,x_1} \beta_{1}(j)$

使用EM算法求解$\vec{\pi}_{\mathrm{ML}}, \mathcal{A}_{\mathrm{ML}}, \mathcal{B}_{\mathrm{ML}}$，关于EM算法的具体介绍可参考文章EM算法和高斯混合模型GMM介绍。具体到该问题，又被称为Forward-Backward Algorithm(i.e., Baum-Welch Algorithm)：

假设参数的当前估计值$\mathcal{\Lambda}^*=[\vec{\pi}^*,\mathcal{A}^*,\mathcal{B}^*]$，则有
- E-step: 定义$q(\vec{s})=p(\vec{s} | \vec{o}, \mathcal{\Lambda}^*)$，则$\mathcal{L}(\mathcal{\Lambda})=\mathbb{E}_{q}[\ln p(\vec{o}, \vec{s} | \mathcal{\Lambda})]$。容易看出$$\ln p(\vec{o}, \vec{s} | \mathcal{\Lambda})= \underbrace{\ln \pi_{s_1}}_{\text{ initial state }} +\sum_{t=2}^{T} \underbrace{\ln \mathcal{A}_{s_{t-1}, s_t}}_{\text { Markov chain }} + \sum_{t=1}^{T} \underbrace{\ln \mathcal{B}_{s_t, x_t}}_{\text { observations }}$$因此$\mathcal{L}$的形式可写为$$\mathcal{L}(\mathcal{\Lambda})=\sum_{k=1}^{S} \gamma_{1}(k) \ln \pi_{k}+\sum_{t=2}^{T} \sum_{j=1}^{S} \sum_{k=1}^{S} \xi_{t}(j, k) \ln \mathcal{A}_{j, k}+\sum_{t=1}^{T} \sum_{k=1}^{S} \gamma_{t}(k) \ln \mathcal{B}_{k, x_{t}}$$其中$\gamma_t(k)=p(s_t=k | \vec{o}, \mathcal{\Lambda}^*),\text{ }\xi_t(j,k)=p(s_{t-1}=j,s_t=k | \vec{o}, \mathcal{\Lambda}^*); \quad 1 \leq t \leq T$，由贝叶斯公式可知$$\begin{cases} \gamma_t(k)=\frac{p(\vec{o}, s_t=k | \mathcal{\Lambda}^*)}{p(\vec{o} | \mathcal{\Lambda}^*)}=\frac{\alpha_t(k)\beta_t(k)}{\sum_{m=1}^S\alpha_t(m)\beta_t(m)} \\ \xi_t(j,k)=\frac{p(\vec{o}, s_{t-1}=j, s_t=k | \mathcal{\Lambda}^*)}{p(\vec{o} | \mathcal{\Lambda}^*)}=\frac{\alpha_{t-1}(j)\mathcal{A}_{jk}^*\mathcal{B}_{k,x_t}^*\beta_t(k)}{\sum_{m=1}^S\alpha_t(m)\beta_t(m)} \end{cases}$$注意此时的$\alpha_t(.)$以及$\beta_t(.)$是从参数的当前估计值$\mathcal{\Lambda}^*$计算出来的
- M-step: 更新参数的估计值$\mathcal{\Lambda}^*=\arg\max_{\mathcal{\Lambda}}\mathcal{L}(\mathcal{\Lambda})$，有$$\pi_{k}^*=\frac{\gamma_{1}(k)}{\sum_{j=1}^S \gamma_{1}(j)}, \quad \mathcal{A}_{jk}^*=\frac{\sum_{t=2}^{T} \xi_{t}(j, k)}{\sum_{t=2}^{T} \sum_{l=1}^{S} \xi_{t}(j, l)}, \quad \mathcal{B}_{kv}^*=\frac{\sum_{t=1}^{T} \gamma_{t}(k) I\left(x_{t}=v\right)}{\sum_{t=1}^{T} \gamma_{t}(k)}$$在实际应用中使用的不仅仅是1个序列，假设有$N$个序列，每个序列的长度为$T_n,\text{ }n\in\{1,2,\cdots,N\}$，则每个序列可以计算出自己的$\gamma_t,\xi_t$，记为$\gamma_t^{(n)},\xi_t^{(n)}$，更新公式变为$$\pi_{k}^*=\frac{\sum_{n=1}^{N} \gamma_{1}^{(n)}(k)}{\sum_{n=1}^{N} \sum_{j=1}^S \gamma_{1}^{(n)}(j)}, \quad \mathcal{A}_{jk}^*=\frac{\sum_{n=1}^{N} \sum_{t=2}^{T_{n}} \xi_{t}^{(n)}(j, k)}{\sum_{n=1}^{N} \sum_{t=2}^{T_{n}} \sum_{l=1}^{S} \xi_{t}^{(n)}(j, l)}, \quad \mathcal{B}_{kv}^*=\frac{\sum_{n=1}^{N} \sum_{t=1}^{T_{n}} \gamma_{t}^{(n)}(k) I\left(x_{t}^{(n)}=v\right)}{\sum_{n=1}^{N} \sum_{t=1}^{T_{n}} \gamma_{t}^{(n)}(k)}$$

迭代上述步骤直到收敛为止

隐藏状态序列估计

为了解决问题2，仍使用动态规划的思想(Viterbi Algorithm)，定义$v_{t}(j)=\max _{s_{1}, \ldots, s_{t-1}} p\left(s_{1}, \ldots s_{t-1}, x_{1}, x_{2}, \ldots x_{t}, s_{t}=j | \mathcal{\Lambda}\right)$，此外还要定义$b_t(j)$用来存储$v_{t}(j)$对应的$s_{t-1}$，则算法可以写为

Initialization: $$v_1(j)=\pi_j\mathcal{B}_{j,x_1},\text{ }b_1(j)=0; \quad 1 \leq j \leq S$$
Recursion: $$\begin{aligned} v_{t}(j) &=\max _{i\in\{1,2,\cdots,S\}} v_{t-1}(i) \mathcal{A}_{i j} \mathcal{B}_{j,x_t} ; \quad 1 \leq j \leq S, 1<t \leq T \\ b_{t}(j) &= \underset{i\in\{1,2,\cdots,S\}}{\arg \max } v_{t-1}(i) \mathcal{A}_{i j} \mathcal{B}_{j,x_t} ; \quad 1 \leq j \leq S, 1<t \leq T \end{aligned}$$
Termination: $$\begin{aligned} & \text { The best score: } P^*=\max _{\vec{s}} p\left(\vec{s},\vec{o} | \mathcal{\Lambda} \right)=\max _{i\in\{1,2,\cdots,S\}} v_{T}(i) \\ & \text { The start of backtrace: } s_{T}^*=\underset{i\in\{1,2,\cdots,S\}}{\operatorname{argmax}} v_{T}(i) \end{aligned}$$
Backtrace: $$s_{t}^*=b_{t+1}(s_{t+1}^*); \quad 1 \leq t<T$$则$s_1^*,s_2^*,\ldots,s_T^*$即为$\arg\max _{\vec{s}} p\left(\vec{s},\vec{o} | \mathcal{\Lambda} \right)$，容易看出$\arg\max _{\vec{s}} p\left(\vec{s},\vec{o} | \mathcal{\Lambda} \right)=\arg\max _{\vec{s}} p\left(\vec{s} | \vec{o}, \mathcal{\Lambda} \right)$

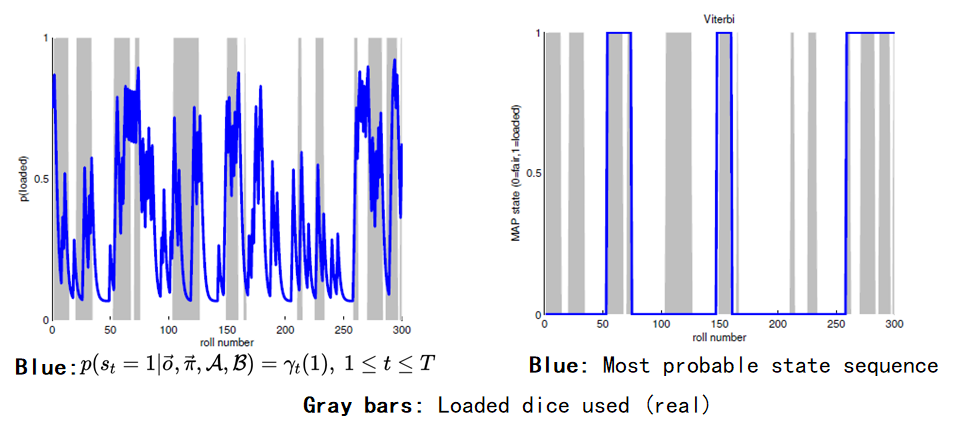
下面介绍一个使用HMM的简单例子：假设有两个骰子，一个未经处理（fair, 记为0），一个经过处理（loaded, 记为1）。每次投掷时使用前一次投掷的骰子，或者使用另一个骰子，观测序列是多次投掷所得到的骰子点数序列。假设真实的参数如下图所示，目标是通过观测序列估计真实的参数，进而估计出每次投掷使用的是哪个骰子。

最终的结果如下图所示，右图表示使用Viterbi算法得到的最可能的隐藏状态序列（即每次投掷使用了哪种骰子），注意左图进行简单地四舍五入后的结果不等于右图，因为左图并没有考虑状态之间的关联。