UESTC-1975弗吉桑(回文串,manacher算法)

弗吉桑

Time Limit: 3000 MS     Memory Limit: 64 MB

Submit Status

弗吉桑是一座横跨清水河大草原的活火山，位于子科技大学主楼东北方约 80km 处，主峰海拔 3776m ， 2002 年 8 月经电子科大校土局重新测量后，为 3775.63m 。

闻名全球的弗吉桑是清水河最重要的象征之一，被视为圣山。弗吉桑与大草原、牧犬羊并列为清水河的校园象征……

对不起扯远了。

校土局希望测量弗吉桑的宽度，于是每隔一定距离测量了经过清水河大草原的多个截面中各处的海拔高度。

由于弗吉桑高度对称，所以我们认为截面中最长的连续对称海拔高度子串即为弗吉桑的宽度。注：题目没说弗吉桑就一定长着个山的形状。

由于服务器沉迷运行 Minecraft 无法自拔，导致学校算力不足。校土局希望借用三万女工的力量测量出弗吉桑的宽度。作为万千女工中的一员，你当然希望早点下班回家陪陪丈夫孩子。

你想到了一个绝妙的主意……

说人话：求最长回文串长度

Input

多组测试数据，输入第一行一个小于 100 的正整数 TT 表示测试组数。

对于每组数据，第一行一个正整数 nn ( 1≤n≤1051≤n≤105 ) ，表示某个截面上测量的海拔总个数。

接下来一行包含 nn 个非负整数 hihi ( 0≤hi≤1090≤hi≤109 ) 表示海拔高度。

Output

每组测试数据一行，输出弗吉桑的宽度。

Sample input and output

Sample Input	Sample Output
2 5 1 2 3 2 1 5 1 2 3 2 3	5 3

Hint

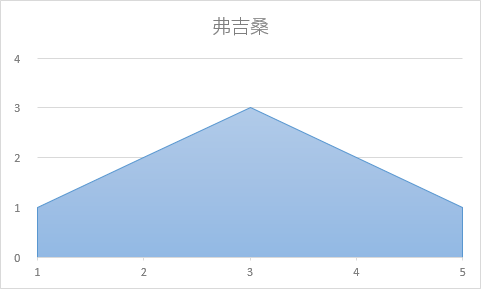
样例第一组数据：

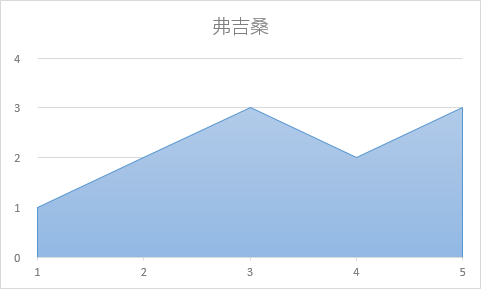
样例第二组数据：

Source

2018 UESTC ACM Training for Search Algorithm and String    

ac代码为：

#include<bits/stdc++.h>
using namespace std;
const int maxn=3e5;
int s[maxn],str[maxn];
int p[maxn],len2,len1;
void init(int n)
{
    len1=n;
    str[0]=-1;
    for(int i=1;i<=2*len1;i+=2)
    {
        str[i]=-2;
        str[i+1]=s[i/2];
    }
    str[2*len1+1]=-2;
    str[2*len1+2]=-3;
    //str[2*len1+3]=-4;
    len2=2*len1+1;
}
int manacher()
{
     int mx=0,ans=0,po=0;
     for(int i=1;i<=len2;i++)
     {
         if(mx>i)
         p[i]=min(mx-i,p[2*po-i]);
         else
         p[i]=1;
         while(str[i-p[i]]==str[i+p[i]]) p[i]++;
         if(p[i]+i>mx)
         {
             mx=p[i]+i;
             po=i;
         }
         ans=max(ans,p[i]);
     }
     return ans-1;
}
int main()
{
    int T,n,num;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        for(int i=0;i<n;i++) scanf("%d",&num),s[i]=num;
        init(n);
        printf("%d\n",manacher());
    }
    return 0;
}