统计学习方法与Python实现（三）——朴素贝叶斯法

　　iwehdio的博客园：https://www.cnblogs.com/iwehdio/

1、定义

　　朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。

　　对于给定的训练数据集，首先基于特征条件独立假设学习输入输出的联合概率分布。然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出y，从而进行决策分类。

　　朴素贝叶斯法学习到的是生成数据的机制，属于生成模型。

　　设Ω为试验E的样本空间，A为E的事件，B1~Bn为Ω的一个划分，则有全概率公式：

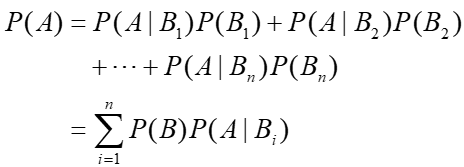
2、学习与分类

　　对于训练数据集：。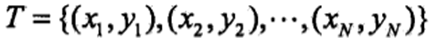

　　我们的目的是从训练集中学习到联合概率分布P(X, Y)，为此先学习后验概率分布和条件概率分布。

　　后验概率分布，即类标签Y的概率分布，条件概率分布即在类标签Y确定的情况下输入特征向量x的分布。

　　从中学习后验概率分布：

　　从中学习条件概率分布：

　　条件概率分布的参数是指数级数量的，对其进行参数估计是不可能的。因此，对条件概率分布做独立性假设，认为输入特征向量x的各个分量是独立的，这也是“朴素”的含义。这样做简化了模型，但是也牺牲了分类的准确率。

　　条件独立性假设：

　　朴素贝叶斯法进行分类时，对于输入特征向量x，通过学习到的模型计算后验概率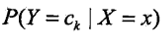。主要是之前学习的后验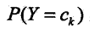概率和条件概率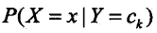，带入全概率公式，可得输入x的条件下，输出y取各个值的概率，并且将概率最大的y作为分类结果。

　　朴素贝叶斯法分类的基本公式为：

　　朴素贝叶斯分类器为：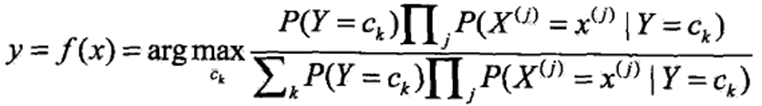

　　分母为定值，则进一步简化可得：

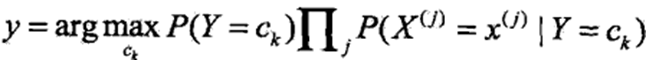
3、分类方法的含义

　　一般的分类方法都有损失函数的概念，优化的目标也是最小化损失函数。朴素贝叶斯法直接要求将实例分到后验概率最大的类中有何含义？实际上，这也等价于期望风险即损失函数最小化。

　　如果对模型f(X)取0-1损失函数L(Y,f(X))，即分类正确损失L取0，分类错误L取1。则期望风险函数为：

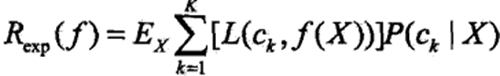
　　因为每个输入特征向量x是独立的，因此只需对每个X=x的实例进行极小化。

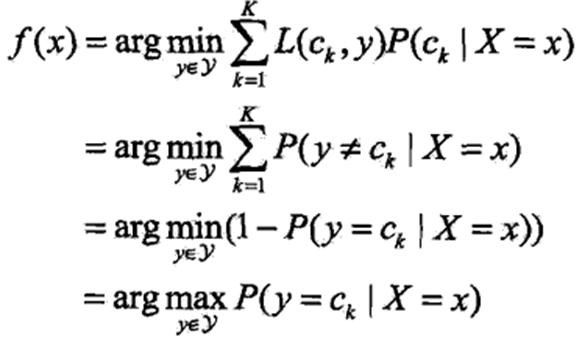
　　即推导得到了后验概率最大化准则。

4、参数学习

　　参数学习即确定每个先验概率和条件概率，一般用极大似然估计法。

　　先验概率P(Y = ck)的极大似然估计是：

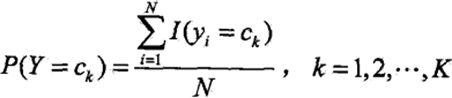　　条件概率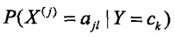（即Y取ck时X的第j个特征取第l个值的概率）的极大似然估计是：

　　其中，函数I(.)表示当括号内的条件满足取1，不满足取0。

　　朴素贝叶斯算法为：

　　a、对于给定的训练数据集，计算先验概率和条件概率。

，

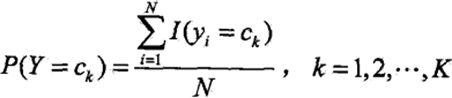　　b、对于给定的实例x，计算

　　c、确定实例x的类

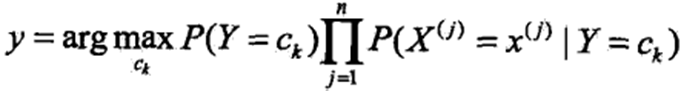
5、贝叶斯估计

　　极大似然估计可能会使所要估计的概率为0的情况，这时会导致计算条件概率时分母为0，使分类出现偏差。可以用贝叶斯估计来解决此问题，即在随机变量各个取值的聘书上加一个正数λ。λ取0时为极大似然估计，λ取1时为拉普拉斯平滑。贝叶斯估计下的条件概率为：

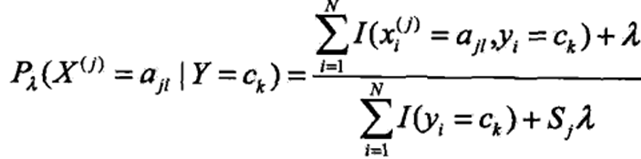
　　贝叶斯估计下的先验概率为：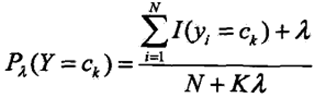

6、Python实现

　　数据集选择mnist手写数字集，数据集中为0~255的整数，先读入数据并对其进行0-1二值化。并初始化数组记录条件概率和先验概率。

from tensorflow.keras.datasets import mnist

import numpy as np

(train_data, train_label), (test_data, test_label) = \

    mnist.load_data(r'E:\code\statistical_learning_method\Data_set\mnist.npz')

# 训练集和测试集大小

train_length = 60000

test_length = 10000

size = 28 * 28      # 输入特征向量长度

data_kind = 10      # 分为几类

choice = 2          # 每个向量有几种取值

lam = 1             # 贝叶斯估计中的lamda

# 预处理数据

train_data = train_data[:train_length].reshape(train_length, size)

# 数据二值化

np.place(train_data, train_data > 0, 1)

train_label = np.array(train_label, dtype='int8')

train_label = train_label[:train_length].reshape(train_length, )

test_data = test_data[:test_length].reshape(test_length, size)

np.place(test_data, test_data > 0, 1)   # 数据二值化

test_label = np.array(test_label, dtype='int8')

test_label = test_label[:test_length].reshape(test_length, )

# 初始化数组记录条件概率和先验概率

P_con = np.zeros([data_kind, size, choice])

P_pre = np.zeros(data_kind)

　　然后在训练集上进行学习，计算先验概率和条件概率。

# 计算先验概率

def compute_P_pre(label, P_init, lamda=1):

    pre = P_init

    for la in label:

        pre[int(la)] += 1

    pre += lamda

    return pre / (label.shape[0] + pre.shape[0] * lamda)

# 计算条件概率

def compute_P_con(data, label, P_init, lamda=1):

    con = P_init

    summ = np.zeros(P_init.shape[0])

    for index, value in enumerate(data):

        for jndex, dalue in enumerate(value):

            con[int(label[index]), jndex, int(dalue)] += 1

        summ[int(label[index])] += 1

    con += lamda

    summ += lamda * 2

    for index, value in enumerate(con):

        con[index] /= summ[index]

    return con

　　最后，在测试集上进行测试。

# 进行测试

def Bayes_divide(pre, con, test, label):

    acc = 0

    ans = np.full(test.shape[0], -1)

    P_div = np.ones([test.shape[0], pre.shape[0]])

    for index, value in enumerate(test):

        for times in range(pre.shape[0]):

            for jndex, dalue in enumerate(value):

                P_div[index, times] *= con[times, jndex, int(dalue)]

            P_div[index, times] *= pre[times]

    for index, temp in enumerate(P_div):

        ans[index] = temp.argmax()

        if ans[index] == label[index]:

            acc += 1

    return acc / label.shape[0], ans

P_pre = compute_P_pre(train_label, P_pre, lamda=lam)

P_con = compute_P_con(train_data, train_label, P_con, lamda=lam)

acc, ans = Bayes_divide(P_pre, P_con, test_data, test_label)

print('acc', acc)

　　lam=1时的测试结果为acc=0.8413。

　　更改lam的值，lam=0时，acc=0.8410；lam=2时，acc=0.8411；lam=5时，acc=0.8407；lam=10时，acc=0.8399。总的而言影响不大。

7、生成模型

　　因为朴素贝叶斯方法是生成模型，所以可以通过训练好的模型生成出模型学习到的特征，也就是生成模型认为最像某个数字的图像。最简单的思想就是，因为我们假设输入特征向量x的各个维度的值是独立的，所以可以输入一个初始向量，然后比较每个维度上取0或1时，模型输出的概率大小，然后将各个维度的值置为更大的概率所对应的值。代码实现如下：

from skimage import io

import matplotlib.pyplot as plt

# 测试输入数据被识别为goal的概率

def test(data0, goal, pre, con):

    P_gene = 1

    for index, value in enumerate(data0):

        P_gene *= con[goal, index, int(value)]

    P_gene *= pre[goal]

    return P_gene

# 初始化输入为全0向量

gene = np.zeros([data_kind, size])

for goals, sim in enumerate(gene):

    temp = sim

    # 遍历向量

    for index in range(sim.shape[0]):

        ans1 = test(temp, goals, P_pre, P_con)

        temp[index] = 1

        ans2 = test(temp, goals, P_pre, P_con)

        if ans1 > ans2:

            temp[index] = 0

# 画出生成的图像

for i in range(gene[:10].shape[0]):

    draw = gene[i][:, np.newaxis]

    draw = draw.reshape([28, 28])

    plt.subplot(1, 10, i+1)

    plt.axis('off')

    io.imshow(draw)

plt.tight_layout()

　　最后的输出结果为：

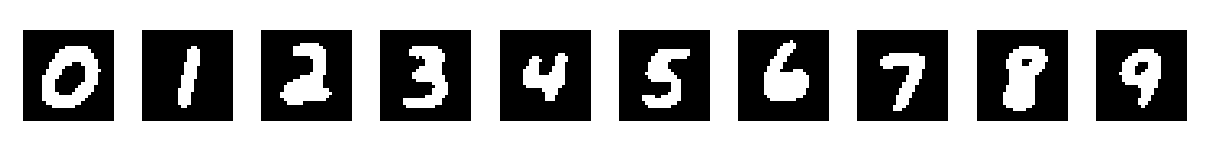
参考：李航《统计学习方法（第二版）》