[考试反思]1030csp-s模拟测试94：未知

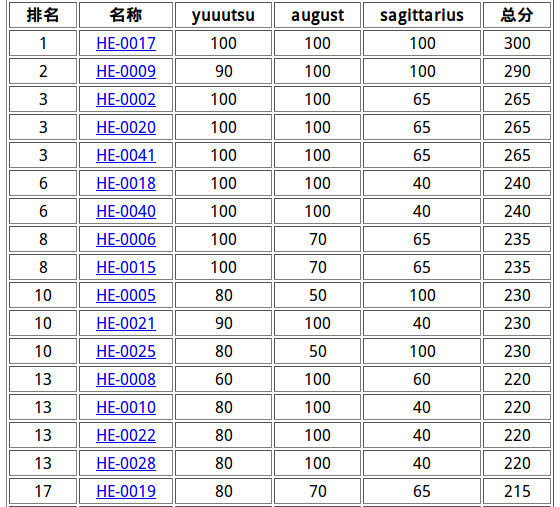
排名也未知。第1或第5。

分数也未知，300或260。

人生真是大起大落。。。

啊啊啊啊啊我好感动啊竟然重测了一次～～～～～

评测机怎么测怎么RE，本机怎么测怎么AC（任意编译指令，任意评测平台）

结果原来是系统栈空间开小了导致递归爆栈了啊。

重测就是把栈空间开到内存限制的大小然后我的代码就没锅了。

然后去隔壁用评测机调了一个小时也找不到RE的原因。。。

也许是对考场上全程无摸鱼一直在思考的奖励吧。。。

然而B哥又被防AK了也是稍惨。

人生第一次AK非B组题，还是有一点激动。。。

出题人部分分给的很好，难得有提示意义。

好事就是让我这个傻子也想出来了，坏事就是所有人的分数都很高%%%。

所以想在总分上凭这一场来翻身还是妄想。

继续加油，没有懈怠的机会。

毕竟又不是谁都像skyh一样两场不考都对排名没影响。。。

upd：人生真是大起大落我又260了没AK我感觉我在farting。。。为什么要这么调戏我的感情啊。。。

T1：凉宫春日的忧郁

写高精就好了，留300位精度绝对炸不了。

其实double就够了。求log精度更高。（好像并没有300位+比较位数的精度高）

 //remember to submit
 #include<cstdio>
 int max(int a,int b){return a>b?a:b;}
 struct Int{
     long long a[];int ws;
     #define mod 1000000000000
     friend void operator*=(Int &x,int p){
         int W=max(x.ws-,);
         for(int i=x.ws;i>=W;--i)x.a[i]*=p;
         for(int i=W;i<=x.ws;++i)x.a[i+]+=x.a[i]/mod,x.a[i]%=mod;
         if(x.a[x.ws+])x.ws++;
     }
     friend bool operator<=(Int x,Int y){
         if(x.ws!=y.ws)return x.ws<y.ws;
         for(int i=x.ws;~i;--i)if(x.a[i]!=y.a[i])return x.a[i]<y.a[i];
         return true;
     }
     void reset(){
         for(int i=ws;~i;--i)a[i]=;
         ws=;a[]=;
     }
 }fc,pw;
 int main(){
     freopen("yuuutsu.in","r",stdin);
     freopen("yuuutsu.out","w",stdout);
     int t,x,y;scanf("%d",&t);
     while(t--){
         scanf("%d%d",&x,&y);
         fc.reset();pw.reset();
         while(y--)fc*=y+,pw*=x;
         puts(pw<=fc?"Yes":"No");
     }
 }

T2：漫无止境的八月

差分。之后操作就是在相距k的位置上一加一减。

其它位互不影响。所以把数组下标直接对k取模即可。

差分的特殊之处在于如果你对序列末尾操作的话会在位置n+1进行加减，而这个位置是几其实是没有关系的。

所以同余于n+1的位置是否为0不会对答案产生影响。特判。

修改的话差分数组只改变了两个位置，判断是否有新的0出现或消失即可。

 //remember to submit
 #include<cstdio>
 int n,k,q,cnt,p;long long x[];
 int read(){
     register int p=,nt=;register char ch=getchar();
     while(ch<''||ch>'')nt=ch=='-',ch=getchar();
     while(ch<=''&&ch>='')p=(p<<)+(p<<)+ch-,ch=getchar();
     return nt?-p:p;
 }
 int main(){
     freopen("august.in","r",stdin);
     freopen("august.out","w",stdout);
     n=read();k=read();q=read();
     for(int i=;i<=n;++i)x[i]=read();
     for(int i=n;i;--i)x[i]=x[i]-x[i-];
     for(int i=k;i<=n;++i)x[i%k]+=x[i];
     for(int i=;i<k;++i)if(x[i])cnt++;
     p=(n+)%k;
     if(x[p])cnt--;
     puts(cnt?"No":"Yes");
     for(int i=,a,b,p1,p2;i<=q;++i){
         a=read(),b=read();
         p1=a%k;p2=(a+)%k;
         if(p1!=p&&x[p1])cnt--;
         if(p2!=p&&x[p2])cnt--;
         x[p1]+=b;x[p2]-=b;
         if(p1!=p&&x[p1])cnt++;
         if(p2!=p&&x[p2])cnt++;
         puts(cnt?"No":"Yes");
     }
 }

T3：射手座之日

我复杂度是错的，极端情况下是$O(\frac{n^2}{k})$，其中k是一个基于数据的常数

具体范围我也不知道，我只知道$4 \leq k  \leq n$

但是可以优化到稳定的$O(nlogn)$，常数会很大，和B哥一样。

看特殊性质部分分，a序列就是dfs序。

那么问题就是对于每一个子区间[l,r]找到最大的p满足$dfn[p]<=l$且$r<=dfr[p]$

其中$dfn/dfr$表示p子树的dfs序区间。

而“最大这个限制不好处理，我们把权值做一遍树上差分，这样的话问题就转化成了：对于每一个子区间[l,r]找到所有的p满足$dfn[p]<=l$且$r<=dfr[p]$

枚举p，它的控制区间内的所有子区间都满足条件，那么答案就是

$\sum\limits_{i=1}^{n} \frac{y[i] \times (dfr[i]-dfn[i]+1) \times (dfr[i]-dfn[i]+2)}{2}$

其中$y$就是$x$数组在树上差分之后的数组，即$y[i]=x[i]-x[f_i]$

而没有了特殊性质之后怎么做？

外层还是枚举p的话，内层的式子就不一样了，是满足上面条件的子区间数。

其实不考虑有包含关系的子区间，那么答案就是$y[i] \times \sum \frac{(r-l+1)\times(r-l+2)}{2}$

问题在于求出所有极长子区间。（极长是指不被包含的区间，如[l,r]存在时[l,r-1]不可能存在，而[1,4][7,9]可以共存）

把问题带到树上，考虑一个叶子节点，它的合法区间就是一个点。

其实对于每一个点它最开始的合法区间都是自己那一个点，后面还要合并上子树内的所有点。

考虑怎么合并。

因为a是一个排列，所以这些区间当然不会有交集，那么我们可以用一个类似与归并排序的过程来合并区间。

合并的过程中如果遇到$[L,p]+[p+1,R]$这样的两个区间，那么就把它合并成一个。

在回溯的同时统计$vector$里面的所有极长区间累加答案即可。

当然这个复杂度不对，虽然也不是很好卡（出题人想不到有这种打法）

然而正解的一种是不再用$vector$归并，而是直接用树上线段树启发式合并来维护极长区间。

时间复杂度是$O(nlogn)$的。

因为LNC说我数据结构必挂所以考场上还真的没有打数据结构2333

 //remember to submit
 #include<cstdio>
 #include<vector>
 #include<algorithm>
 using namespace std;
 vector<int>L[],R[],reL,reR;
 int ec,fir[],l[],to[],x[],y[],dfn[],dfr[];
 int a[],tim,n,pos[];long long ans;
 void link(int a,int b){l[++ec]=fir[a];fir[a]=ec;to[ec]=b;}
 void dfs(int p,int fa){
     y[p]=x[p]-x[fa]; dfn[p]=++tim;
     for(int i=fir[p];i;i=l[i])if(to[i]!=fa)dfs(to[i],p);
     dfr[p]=tim;
 }
 void pushin(int l,int r){
     if(reL.empty()||reR[reR.size()-]!=l-)return reL.push_back(l),reR.push_back(r),(void);
     reR[reR.size()-]=r;
 }
 void DFS(int p,int fa){
     L[p].push_back(pos[dfn[p]]);R[p].push_back(pos[dfn[p]]);
     for(int i=fir[p];i;i=l[i])if(to[i]!=fa){
         DFS(to[i],p);
         int p1=,p2=,e1=L[p].size(),e2=L[to[i]].size();
         while(p1<e1&&p2<e2)if(L[p][p1]<L[to[i]][p2])pushin(L[p][p1],R[p][p1]),p1++;
             else pushin(L[to[i]][p2],R[to[i]][p2]),p2++;
         while(p1<e1)pushin(L[p][p1],R[p][p1]),p1++;
         while(p2<e2)pushin(L[to[i]][p2],R[to[i]][p2]),p2++;
         swap(reL,L[p]);swap(reR,R[p]);
         reL.clear();reR.clear();L[to[i]].clear();R[to[i]].clear();
     }int sz=L[p].size();
     for(int i=;i<sz;++i)ans+=(R[p][i]-L[p][i]+1ll)*(R[p][i]-L[p][i]+2ll)/*y[p];
 }
 int main(){
     freopen("sagittarius.in","r",stdin);
     freopen("sagittarius.out","w",stdout);
     scanf("%d",&n);
     for(int i=,f;i<=n;++i)scanf("%d",&f),link(f,i);
     for(int i=;i<=n;++i)scanf("%d",&a[i]);
     for(int i=;i<=n;++i)scanf("%d",&x[i]);
     dfs(,);
     for(int i=;i<=n;++i)a[i]=dfn[a[i]],pos[a[i]]=i;
     DFS(,);
     printf("%lld\n",ans);
 }