前端与算法 leetcode 48. 旋转图像

目录

• 前端与算法 leetcode 48. 旋转图像
  • 题目描述
  • 概要
  • 提示
  • 解析
    • 解法一:转置加翻转
    • 解法二:在单次循环中旋转 4 个矩形
  • 算法
  • 传入测试用例的运行结果
  • 执行结果
  • GitHub仓库

前端与算法 leetcode 48. 旋转图像

---

题目描述

给定一个 n × n 的二维矩阵表示一个图像。

将图像顺时针旋转 90 度。

说明：

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例 1:

给定 matrix =
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],

原地旋转输入矩阵，使其变为:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

示例 2:

给定 matrix =
[
  [ 5, 1, 9,11],
  [ 2, 4, 8,10],
  [13, 3, 6, 7],
  [15,14,12,16]
], 

原地旋转输入矩阵，使其变为:
[
  [15,13, 2, 5],
  [14, 3, 4, 1],
  [12, 6, 8, 9],
  [16, 7,10,11]
]

48. 旋转图像

概要

这道题只要不是做太多的操作,往往都能达到O1的复杂度

提示

转置,逆序

解析

解法一:转置加翻转

最直接的想法是顺时针旋转90度，可以根据转置矩阵的性质，先得到转置矩阵，再进行列交换，即可实现这个简单的方法已经能达到最优的时间复杂度O(N^2)。

解法二:在单次循环中旋转 4 个矩形

解法一使用了两次矩阵操作，但是有只使用一次操作的方法完成旋转。仔细思考每个元素在旋转中如何移动



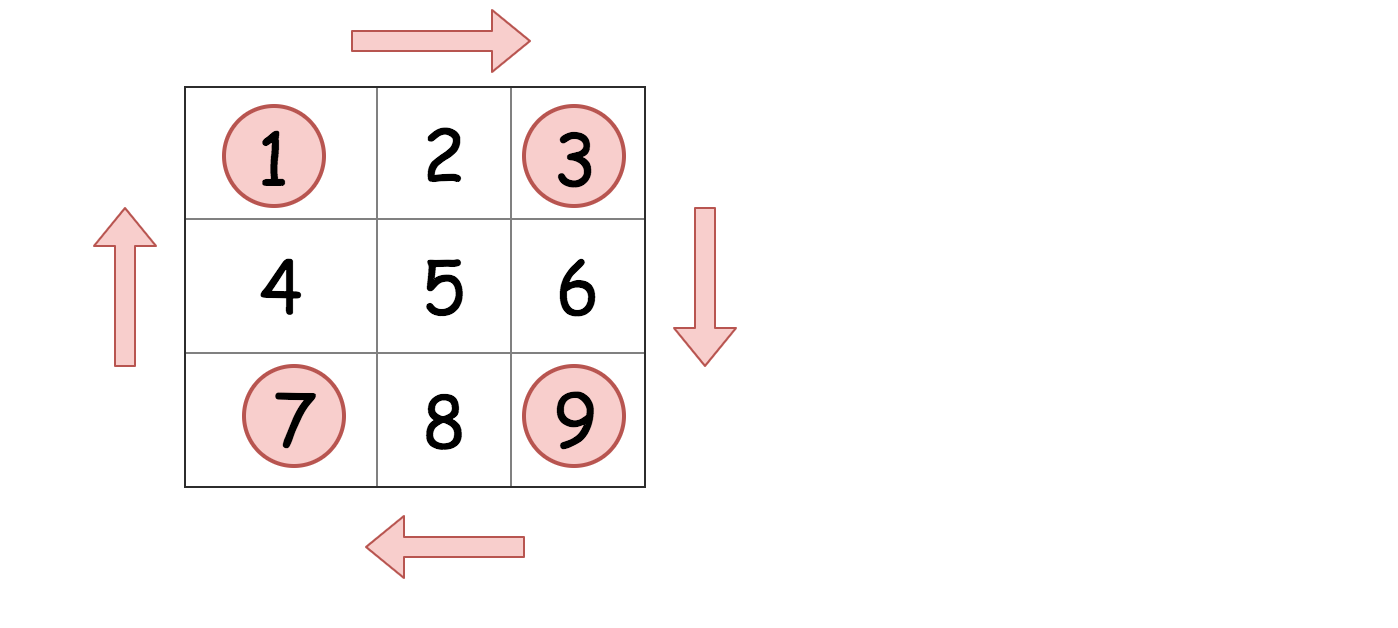
这提供给我们了一个思路，将给定的矩阵分成四个矩形并且将原问题划归为旋转这些矩形的问题。



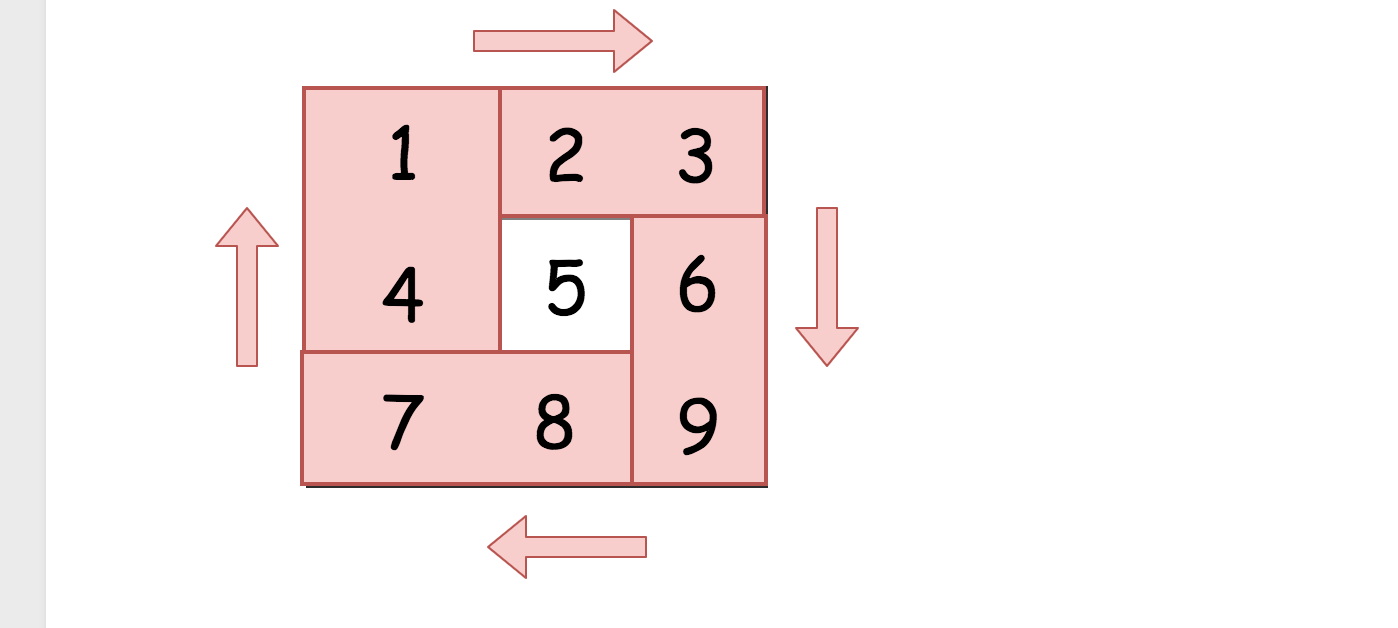
现在的解法很直接 - 可以在第一个矩形中移动元素并且在 长度为 4 个元素的临时列表中移动它们。

算法

/**
 * @param {number[][]} matrix
 * @return {void} Do not return anything, modify matrix in-place instead.
 */
var rotate = function (matrix) {
  // 使用数组暂存
  // const len = matrix.length - 1;
  // let changeRow = [];
  // for (var i = 0; i <= len; i++) {
  //     for (var j = 0; j <= len; j++) {
  //         changeRow[j] = changeRow[j] || [];
  //         changeRow[j][len - i] = matrix[i][j];
  //     }
  // }
  // matrix.length = 0;
  // matrix.push(...changeRow); // 重写
  // 在单次循环中旋转 4 个矩形
  let len = matrix.length - 1;
  for (let row = 0;row < len / 2;row++) {
    for (let col = row;col < len - row;col++) {
      let tmp = matrix[row][col];
      matrix[row][col] = matrix[len - col][row];
      matrix[len - col][row] = matrix[len - row][len - col];
      matrix[len - row][len - col] = matrix[col][len - row];
      matrix[col][len - row] = tmp;
    }
  }
  // 转置加翻转
  // let len = matrix.length;
  // // 转置矩阵
  // for (let i = 0;i < len;i++) {
  //     for (let j = i;j < len;j++) {
  //         [matrix[j][i], matrix[i][j]] = [matrix[i][j], matrix[j][i]];
  //     }
  // }
  // // 翻转行
  // for (let i = 0;i < len;i++) {
  //     for (let j = 0;j < len / 2;j++) {
  //         [matrix[i][j], matrix[i][len - j - 1]] = [matrix[i][len - j - 1], matrix[i][j]];
  //     }
  // }
};

传入测试用例的运行结果

input:[[1, 2, 3], [4, 5, 6], [7, 8, 9]]
output:[ [ 7, 4, 1 ], [ 8, 5, 2 ], [ 9, 6, 3 ] ]

执行结果

执行用时 :60 ms, 在所有 javascript 提交中击败了90.96%的用户
内存消耗 :33.4 MB, 在所有 javascript 提交中击败了95.92%的用户

GitHub仓库

48. 旋转图像