SIGAI机器学习第十九集 随机森林

讲授集成学习的概念，Bootstrap抽样，Bagging算法，随机森林的原理，训练算法，包外误差，计算变量的重要性，实际应用

大纲：

集成学习简介

Boostrap抽样

Bagging算法

随机森林的基本原理

训练算法

包外误差

计算变量的重要性

实验环节

实际应用

随机森林是一种集成学习的算法，构建在bootstrap采样基础之上的，bagging算法基于boostrap采样，与之对应的是boosting算法。随机森林是多颗决策树的集成，由于采用了bootstrip采样，在训练时有一部分样本是没有被选中的，这些样本称为包外样本，训练完一个决策树之后可以测试这个样本集的误差，称为包外误差。

集成学习简介：

集成学习（ensemble learning）是机器学习中的一种哲学思想，它通过多个模型的组合形成一个精度更高的模型，参与组合的模型称为弱学习器（weaker learner），组合之后的模型称为强学习器，精读不是很高的弱学习器集成起来之后能够显著提高算法精度。

在预测时使用这些弱学习器模型联合进行预测，如Bagging是弱学习器联合起来进行投票，Boosting算法是用弱学习器的加权和来表示的。

训练时需要用训练样本依次训练出这些弱学习器，每个弱学习器用不同的样本集训练，如将训练集D分为D1、D2、...，分别用于训练弱学习器1、弱学习器2、...。

Bagging算法和Boosting算法是集成学习的两个典型的实现，他们是两个抽象的框架，如果把他们具体实现出来的话，有两种典型的算法，分别是随机森林（它的弱学习器是决策树）和AdaBoost算法（每个弱学习器带有权重值，有时候为了计算效率也用决策树作为弱学习器）。

Boostrap抽样：

抽样在统计学中的精髓就是从样本来推断整体的情况，选取一些随机的样本出来，它们来代表整体的一些信息，，通过研究这些样本来知道整体是一个什么结构。

所谓抽样是指从一个样本数据集中随机选取一些样本，形成新的数据集。
有放回抽样，一个样本被抽中之后会放回去，在下次抽样时还有机会被抽中。
无放回抽样，一个样本被抽中之后就从抽样集中去除，下次不会再参与抽样，因此一个样本最多只会被抽中一次。

Bootstrap是有放回抽样，从n个样本中有放回的抽取出n个样本。

一个样本每次都不被抽中的概率为(1-1/n)ⁿ

当样本数很大的时候，这个概率近似等于1/e，lim_n->+∞(1-1/n)ⁿ = 1/e

所以当样本数n足够大时，在整个抽样中所有样本大约有36.8%没有被抽中。这部分样本称为包外（Out Of Bag，简称OOB）。

Bagging算法：

有了Boostrap有放回的抽样之后，可以以它为基础，可以构造出Bagging算法这种抽象的集成学习框架。

Bagging算法，一次训练T个弱学习器，对于分类问题称为弱分类器（因为我们处理的大部分是分类问题），它怎么做的呢？

循环依次训练这T个模型，怎么训练呢？首先对样本集进行Boostrap抽象抽一些样本出来D1、D2、...，用Di训练第i个弱学习器模型hi(x)，训练完之后就输出一个这些模型的组合，对于分类问题对它进行投票就可以了。

随机森林的基本原理：

Bagging算法只是一个抽象的框架，并没有指明我们的弱学习器是什么类型的，用线性分类器也好，用决策树也好，比如像用贝叶斯、SVM等都是可以的。

如果弱学习器是采用决策树的Bagging算法，那这种算法就称为随机森林。

随机森林由Breiman等人提出，它由多棵决策树组成，分类与回归树CART的发明人也是Breiman。

对于分类问题，一个测试样本会送到每一棵决策树中进行预测，然后投票，得票最多的类为最终分类结果。
对于回归问题随机森林的预测输出是所有决策树输出的均值，同K近邻算法类似。

使用多棵决策树联合进行预测可以降低模型的方差（方差反应机器学习算法输出值的波动程度），假设每一个决策树的输出值是一个随机变量，对于回归问题，则最终随即森林的输出值是它们的均值（加起来除以n，除不除都无所谓 ）。概率论数理统计中有一个重要结论，n个随机变量xi之间独立同分布，那么他们之和的方差等于它们各自的方差平方除以n，即你加进来的变量xi越多，它们最终的方差会越小，一个人可能会犯错误，但是多个人一起来决策取均值的话，那一个xi犯错误在里边占的影响就非常小了，一个变量xi犯正错误，一个人犯负错误，最终可以抵消掉，也就是弱学习器决策树越多，我们的随机森林方差越小。

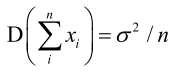
训练算法：

训练时依次训练每一棵决策树，每棵树的训练样本都是从原始训练集中进行随机抽样得到（有放回抽样随机抽出一部分样本和无放回抽样随机抽出向量的一些特征分量）。

在训练决策树的每个节点时所用的特征也是随机抽样得到的，即从特征向量中随机抽出部分特征参与训练。

随机森林对训练样本和特征向量的分量都进行了随机采样。

样本的随机抽样可以用均匀分布的随机数构造，如用random(1,n)实现。
对特征分量的采样是无放回抽样，可以用随机洗牌算法实现。

随机森林训练的时候需要确定的参数：一个是决策树的数量，二是选用多少个特征做分裂。

决策树的数量怎么确定？一遍训练一遍测它的精度，如果增加随机森林的决策树的数量它的精度还在上升的话就可以继续加树，直到加到某个临界点再加决策树数量的时候，精度值没有什么改善的时候就可以停下来了。

使用的特征的数量，选用多少个特征的问题，一般按照某个比例选择一部分特征出来就可以了。

包外误差：

训练每一棵决策树时约有部分样本未参与训练。可以在训练时利用这些没有被选中的样本做测试，统计它们的预测误差，这称为包外误差。
包外误差这种方式类似于交叉验证CV，但和交叉验证不同的是，它的训练集中会出现重复样本（因为是有放回抽样），而交叉验证的训练集中无重复样本。

从多次训练来看，二者都是把样本集切分成多份，轮流用其中的一部分样本进行训练，用剩下的样本进行测试，不同的是交叉验证把样本均匀的切分成份，在训练集中同一个样本不会出现多次；后者在每次bootstrap抽样时同一个样本可能会被选中多次。

实际上经验表明，包外误差可以用作交叉验证的结果，可以用来近似替代交叉验证，作为交叉验证的精度值。

包外误差怎么定义呢？

对于分类问题，包外误差定义为被错分的包外样本数与总包外样本数的比值。
对于回归问题，所有包外样本的回归误差和除以包外样本数，就是均方误差。

计算变量的重要性：
随机森林可以计算变量的每一个分量的重要性，重要性怎么计算呢？采用随即置换法。

置换法思想：如果某个特征很重要，那么改变样本的该特征值，该样本的预测结果就容易出现错误，如果一个特征对分类不重要，随便改变它对分类结果没多大影响。

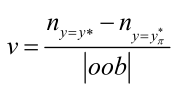
|oob|是包外样本数目，分子第一项是置换变量分量前正确分类的个数，分子第二项是置换变量分量（如x1和x10的值交换）后正确分类的个数。

v这个值越大，说明改变了这个特征分量的值以后对分类结果的影响越大，那该分量就越重要。

上面定义的是单棵决策树的变量重要性，计算出每棵树的变量重要性之后，对该值取平均就得到随机森林的变量重要性。
实验环节：

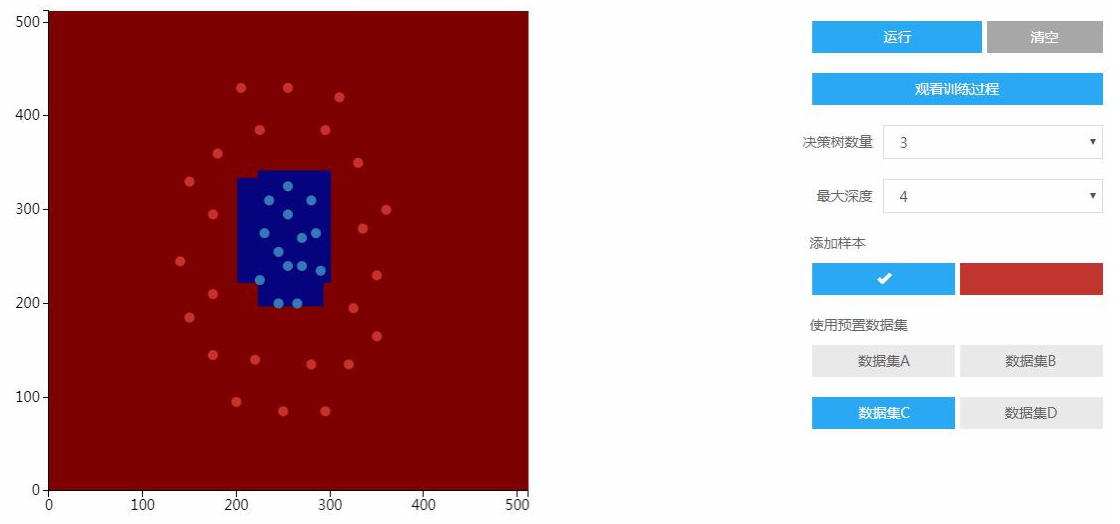
原理性实验的实验目的是知道算法的原理。选好样本，设置好随机森林参数决策树数量和最大深度之后，开始训练出一个模型出来，用该模型进行分类。多棵决策树集成以后和决策树一样，分类边界还是一些折线，还是一个分段的线性函数，分段的线性函数不是线性函数。

训练某棵决策树的时候随机抽取一部分样本来训练一棵决策树出来：

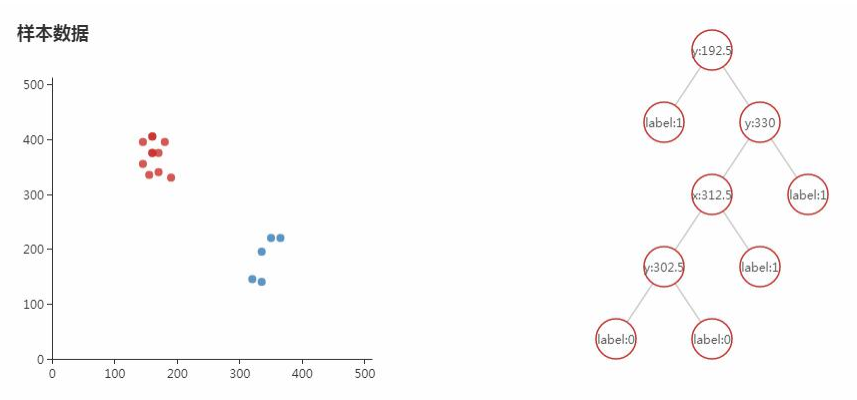
因为我们选择的决策树的数量为3，所以它会进行3次Bootstrap抽样，然后训练3个决策树t1、t2、t3，打印出来可以看到每个形态都是不一样的：

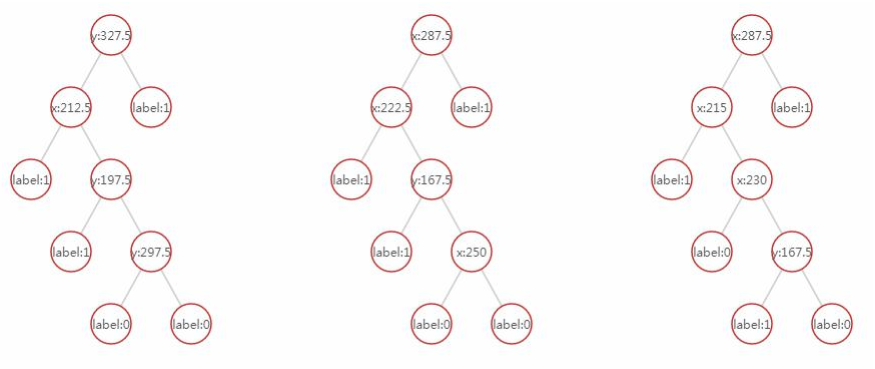
实际应用：

随机森林虽然看上去很简单，它就是巧妙地把多棵决策树集成起来，通过一个随机抽样技术，但是它得到的性能是相当明显的，因此它被广泛地应用到很多领域里面，主要是一些数据预测的问题，根据一组特征向量的值来做分类或回归，下面看一下它的几个典型的应用：

[1] Jisoo Ham, Yangchi Chen, Melba M Crawford, Joydeep Ghosh. Investigation of the random forest framework for classification of hyperspectral data. IEEE Transactions on Geoscience and Remote Sensing.2005.
[2] M Pal. Random forest classifier for remote sensing classification.International Journal of Remote Sensing.2005.

上面两个是在图像识别方面的应用。

[3] Dong Chen, Shaoqing Ren, Yichen Wei, Xudong Cao, Jian Sun. Joint Cascade Face Detection and Alignment. european conference on computer vision. 2014.人脸检测JDA，定位人脸几个关键点，用到了随机森林的思想。

现在还有不少互联网公司，他们的业务使用随机森林实现的，做各种数据的分类和预测，其实核心还是特征工程，只有把特征值构造好了，剩下的就是一个标准的交给随机森林来处理就OK了。

本集总结：

集成学习的概念和思想

Boosting随机抽样的思想

基于Boosting随机抽样的第一种抽象的集成学习框架Bagging算法

Bagging算法的弱学习器选择决策树的话就得到了随机森林RF

随机森林训练算法，对训练样本随机和对特征分量随机（用于节点分裂）

OOB包外误差

实验环节、实际应用

随机森林的两个核心：用Boostrap对样本进行抽样依次训练每个决策树，以及训练每个决策树的过程中对每个特征分量进行抽样，我们寻找最佳分裂的时候只考虑这部分特征就OK了。