spark 机器学习 随机森林 原理(一)

1.什么是随机森林
顾名思义，是用随机的方式建立一个森林，森林里面有很多的决策树组成，随机森林的每一棵决 策树之间是没有关联的。在得到森林之后，当有一个新的输入样本进入的时候，就让森林中的每一棵决策树分别进行一下判断，看看这个样本应该属于哪一类（对于分类算法），然后看看哪一 类被选择最多，就预测这个样本为那一类。
我们可以这样比喻随机森林算法：每一棵决策树就是一个精通于某一个窄领域的专家（因为我们 从M个特征中选择m个让每一棵决策树进行行学习），这样在随机森林中就有了了很多个精通不不同领 域的专家，对一个新的问题（新的输入数据），可以用不不同的角度去看待它，最终由各个专家， 投票得到结果

2.Bootstraping（随机且有放回地抽取）
Leo Breiman于1994年提出的Bagging（又称Bootstrap aggregation，引导聚集）是最基本的集成技术之一。Bagging基于统计学中的bootstraping（自助法），该方法使得评估许多复杂模型的统计数据更可行。
2.1bootstrap方法的流程如下：假设有尺寸为N的样本X。我们可以从该样本中有放回地随机均匀抽取N个样本，以创建一个新样本。换句话说，我们从尺寸为N的原样本中随机选择一个元素，并重复此过程N次。选中所有元素的可能性是一样的，因此每个元素被抽中的概率均为1/N。
2.2假设我们从一个袋子中抽球，每次抽一个。在每一步中，将选中的球放回袋子，这样下一次抽取是等概率的，即，从同样数量的N个球中抽取。注意，因为我们把球放回了，新样本中可能有重复的球。让我们把这个新样本称为X1。
重复这一过程M次，我们创建M个bootstrap样本X1，……，XM。最后，我们有了足够数量的样本，可以计算原始分布的多种统计数据。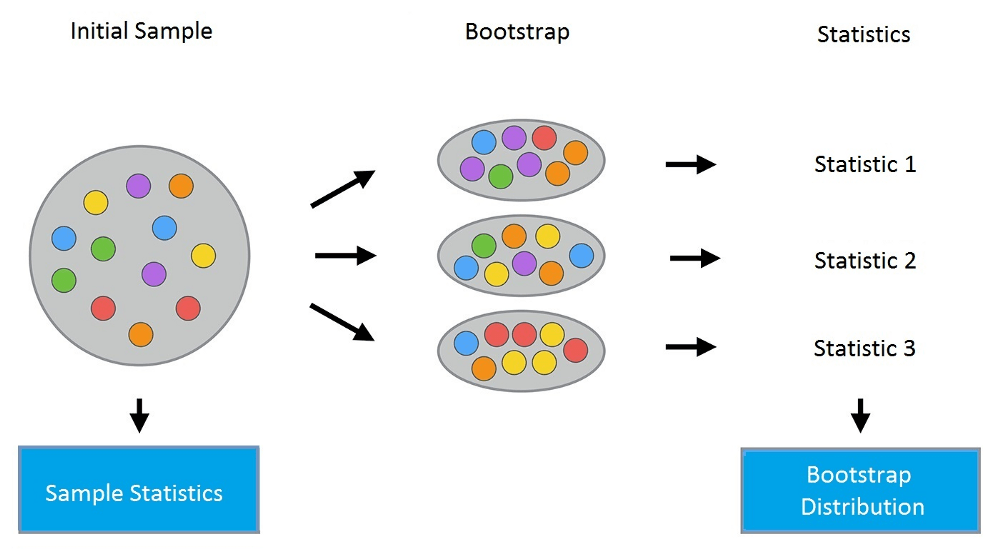

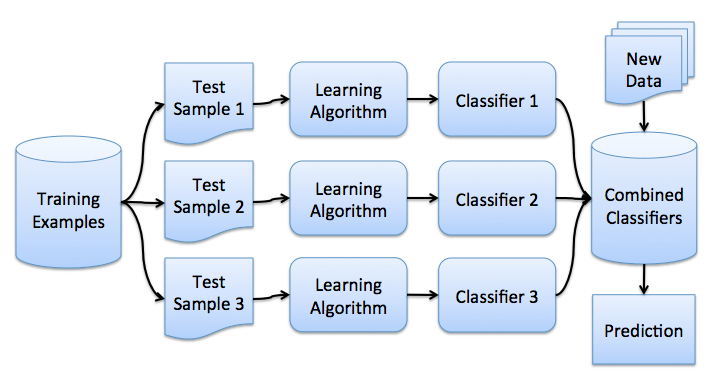
3. Bagging

理解了bootstrap概念之后，我们来介绍bagging。
假设我们有一个训练集X。我们使用bootstrap生成样本X1, …, XM。现在，我们在每个bootstrap样本上分别训练分类器ai(x)。最终分类器将对所有这些单独的分类器的输出取均值。在分类情形下，该技术对应投票（voting）：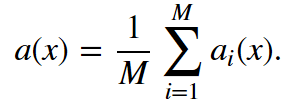

4.袋外误差(OOBE)
我们知道，在构建每棵树时，我们对训练集使用了不同的bootstrap sample（随机且有放回地抽取）。所以对于每棵树而言（假设对于第k棵树），大约有1/3的训练实例没有参与第k棵树的生成，它们称为第k棵树的oob样本。
而这样的采样特点就允许我们进行oob估计，它的计算方式如下：
1对每个样本，计算它作为oob样本的树对它的分类情况（约1/3的树）；
2然后以简单多数投票作为该样本的分类结果；
3最后用误分个数占样本总数的比率作为随机森林的oob误分率。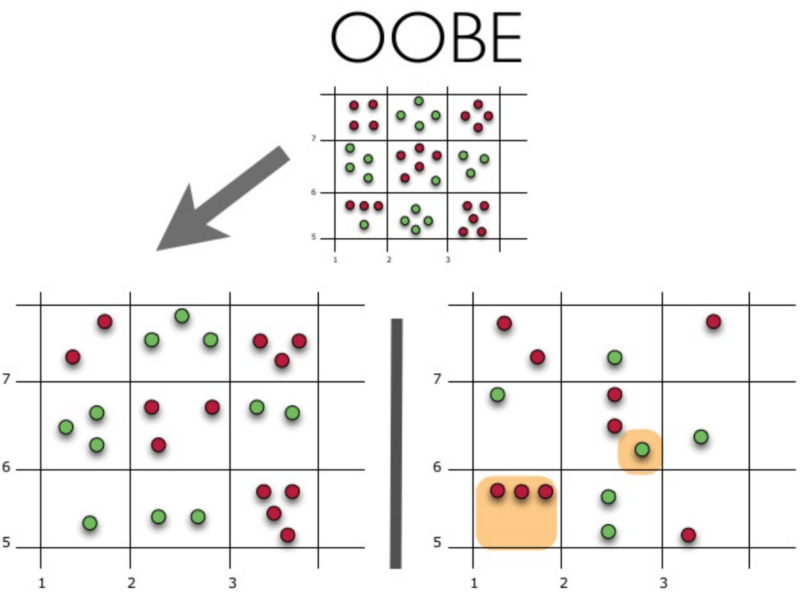

示意图上方为原始数据集。我们将其分为训练集（左）和测试集（右）。在测试集上，我们绘制一副网格，完美地实施了分类。现在，我们应用同一副网格于测试集，以估计分类的正确率。我们可以看到，分类器在4个未曾在训练中使用的数据点上给出了错误的答案。而测试集中共有15个数据点，这15个数据点未在训练中使用。因此，我们的分类器的精确度为11/15 * 100% = 73.33%.

总结一下，每个基础算法在约63%的原始样本上训练。该算法可以在剩下的约37%的样本上验证。袋外估计不过是基础算法在训练过程中留置出来的约37%的输入上的平均估计。

5.随机森林流程
5.1设样本数等于n，特征维度数等于d。
5.2选择集成中单个模型的数目M。
5.3对于每个模型m，选择特征数dm < d。所有模型使用相同的dm值。
5.4对每个模型m，通过在整个d特征集合上随机选择dm个特征创建一个训练集。
5.5训练每个模型。
5.6通过组合M中的所有模型的结果，应用所得集成模型于新输入。