OI数学汇总

前言

　　数学在\(\text{OI}\)中十分重要。其中大多都是数论。

　　什么是数论？

\[研究整数的理论 ——zzq
\]

　　本文包含所有侧边目录中呈现的内容。绝对丰富！！！

　　下面直奔主题。

整除、同余、裴蜀定理、辗转相除法、扩展欧几里得

群

　　\((G,\cdot)\)表示\(G\)对定义在集合\(G\)上的运算\(\cdot\)构成群，它需要满足：

　　（1）封闭性：若\(a,b \in G\)，则存在唯一确定的\(c \in G\)，使得\(a\cdot b=c\)。

　　（2）结合律：对于\(a,b,c \in G : (a\cdot b)\cdot c = a\cdot (b\cdot c)\)

　　（3）存在单位元：存在\(e \in G\)，使得\(\forall a \in G : a\cdot e=e\cdot a\)，\(e\)被称作单位元。

　　（4）存在逆元：\(\forall a \in G, \exist b \in G : a\cdot b=b\cdot a=e\)，\(b\)又写作\(a^{-1}\)。

逆元

欧拉函数

欧拉定理及拓展形式

威尔逊定理

同余方程（组）、中国剩余定理（CRT、EXCRT）

阶和原根

BSGS、exBSGS

剩余问题

　　解决形如\(x^k \equiv a \pmod p\)的问题。暴力找似乎代价太高了。我们先从简单的入手。

二次剩余

　　若\(x^2 \equiv a \pmod p\)有解，则称\(a\)是\(p\)的二次剩余。否则称其为非二次剩余。

　　定义\(\text{Legendre}\)符号：

\[\left( \frac{a}{p} \right)=\begin{cases}
1 & a是p的二次剩余 \\
-1 & a不是p的二次剩余 \\
0 & p \mid a
\end{cases}
\]

　　（长相奇怪，其实只是记号）

　　先讨论\(p\)是奇素数的情况。此时有：

\[\left( \frac{a}{p} \right) \equiv a^\frac{p-1}{2} \pmod p
\]

　　\(Proof\)：

\[当p \mid a时命题显然成立
\]

\[当p \nmid a时，如果a是p的二次剩余，则有x^2\equiv a \pmod p
\]

\[\therefore (x^2)^{\frac{p-1}{2}} \equiv a^{\frac{p-1}{2}} \pmod p
\]

\[\therefore x^{p-1} \equiv a^{\frac{p-1}{2}} \pmod p
\]

\[由费马小定理易知左边同余1，所以右边同余1
\]

\[如果a不是p的二次剩余，则不存在x使得x^2 \equiv a \pmod p成立
\]

\[\because p是奇质数
\]

\[\therefore 一定能找到x \neq y，使得xy \equiv a \pmod p
\]

\[而共有\varphi(p)=p-1个数，其可以两两配对使得上式成立（由逆元的唯一性得到）
\]

\[\therefore (p-1)! \equiv a^{\frac{p-1}{2}} \pmod p
\]

\[又由威尔逊定理得:(p-1)! \equiv -1 \pmod p
\]

\[\therefore a^{\frac{p-1}{2}} \equiv -1 \pmod p
\]

　　我们证明了所有的二次剩余得到的结果都是\(1\)，所有的非二次剩余得到的结果都是\(0\)，而又不存在第三者，所以命题能成立。

　　然后有\(p\)是奇质数下，二次剩余和非二次剩余的数量一样多。这个很显然，让\(1\)到\(p-1\)的平方在模\(p\)意义下构成集合，而我们有：

\[x^2 \equiv (p-x)^2 \pmod p
\]

　　这个东西展开下就证完了，所以我们只要考虑\(1\)到\(\frac{p-1}{2}\)之间的平方即可。

　　若有\(x^2 \equiv y^2 \pmod p\)，\(x \neq y\)，则\(x^2-y^2 \equiv 0 \pmod p \Rightarrow p \mid (x-y)(x+y)\)，由于\(p\)是质数，所以有\(p \mid x-y\)或\(p \mid x+y\)而得到\(x \equiv y\)或\(-y\)，第一种情况不存在，第二种情况发现两数一定不在同一个部分（即在\(\frac{p-1}{2}\)两边），不合假设。所以得到\(1\)到\(\frac{p-1}{2}\)之间，两两的平方不同，而这样得到的二次剩余只有\(\frac{p-1}{2}\)个，非二次剩余也只有\(\frac{p-1}{2}\)个。所以得证。

Cipolla

　　该算法是用来解决二次剩余问题的，思想基于构造。注意下文解决的是\(x^2 \equiv n \pmod p\)，右边的是\(n\)而不是\(a\)了。

　　如果\(n\)是二次非剩余，显然无解；

　　如果\(n\)是二次剩余，我们随机一个\(a\)，使得\(\left( \frac{a^2-n}{2} \right) = -1\)。由非二次剩余和二次剩余数量一样多，所以有\(\frac{1}{2}\)的概率取到，而期望下\(2\)次即能得到。证明不重要，放在后面。定义\(\omega = \sqrt{a^2-n}\)，事实上\(\omega\)在整数域中没有数存在，所以类似于定义虚数单位\(i\)一样，存数也先存成\(a+b\omega\)这种形式，之后会消掉这个东西。

　　我们要\(x^2 \equiv a \pmod p\)，先要知道这几个引理。

　　引理1：\((x+\omega)^p \equiv x^p + \omega^p \pmod p\)。

　　\(Proof\)：

\[由二项式定理得：(x+\omega)^p = \sum_{i=0}^p {p \choose i} x^i\omega^{p-i} \equiv x^p+\omega^p \pmod p
\]

\[中间若干项项由于组合数系数被模掉了，这样就\text{Q.E.D}了
\]

　　引理2：\(\omega^p \equiv -\omega\)。

　　\(Proof\)：

\[注意\omega可能不存在于整数域中，所以我们不能直接运用费马小定理
\]

\[\omega^p = \omega^{p-1}\omega = (\omega^2)^\frac{p-1}{2}\omega = (a^2-n)^\frac{p-1}{2}\omega \equiv -\omega \pmod p
\]

\[这些我们运用的是上面的定义推导出来的
\]

　　结论：\(x=(a+\omega)^\frac{p+1}{2}\)

　　\(Proof\)：

\[(a+\omega)^{p+1} = (a+\omega)^p(a+\omega) = (a^p+\omega^p)(a+\omega)=(a-\omega)(a+\omega)=a^2-\omega^2=a^2-(a^2-n)=n \equiv x^2 \pmod p
\]

\[\Rightarrow (a+\omega)^{p+1} \equiv x^2 \pmod p
\]

\[\Rightarrow x \equiv (a+\omega)^\frac{p+1}{2} \pmod p
\]

\[\text{Q.E.D}
\]

　　那这个式子咋求？直接上复数。根据拉格朗日定理，最后虚部一定为\(0\)。不会拉格朗日定理？其实我也不会那我们反证下吧。

　　\(Proof\)：

\[假设存在x=A+B\omega，B \neq 0，使得x^2 = (A+B\omega)^2 \equiv n \pmod p
\]

\[那么一定有A^2 + 2AB\omega + B^2\omega^2 = A^2 + 2AB\omega + B^2(a^2-n) \equiv n \pmod p
\]

\[\Rightarrow A^2+B^2(a^2-n)-n \equiv -2AB\omega \pmod p
\]

\[\because式子左边的虚部为0，表明式子的右边虚部也为0
\]

\[\therefore必须有:-2AB \equiv 0 \pmod p
\]

\[\because B \not\equiv 0
\]

\[\therefore A \equiv 0
\]

\[\therefore B^2\omega^2 \equiv n \pmod p
\]

\[\therefore \omega^2 \equiv nB^{-2} \pmod p
\]

\[n是二次剩余，B^2是二次剩余，所以B^{-2}也应为二次剩余
\]

\[根据\text{Legendre}符号可以推出二次剩余与二次剩余的积为二次剩余，而\omega^2却不是二次剩余
\]

\[矛盾，所以B=0
\]

　　还有一种情况就是\(p=2\)，此时它是质数但不是奇质数，所以特判掉即可。

　　如果\(x\)有解，其实存在两组解，另一组解为\(p-x\)。

int T, N, P;

namespace Cipo {
#define rd() (1ll * rand() * RAND_MAX + rand()) // 随机数可能范围不够
	int n, P; // x^2=n (%p)
	int a, t; // t = w^2 = a^2-n
	struct comp { // 自定义复数类
		int x, y;
		comp operator * (const comp &rhs) const { // (x1,y1)(x2,y2)=(x1x2+y1y2t,x1y2+x2y1)，这是复数乘，注意取模
			return (comp){(1ll*x*rhs.x + 1ll*y*rhs.y%P*t)%P, (1ll*x*rhs.y+1ll*y*rhs.x)%P};
		}
	};
	comp qpow(comp a, int b) { // 复数类快速乘
		comp res = (comp){1, 0};
		for (comp k = a; b; k = k*k, b >>= 1)
			if (b & 1) res = res*k;
		return res;
	}
	int qpow(int a, int b) { // 普通快速乘
		int res = 1;
		for (register int k = a; b; k = (ll)k*k%P, b >>= 1)
			if (b & 1) res = (ll)res*k%P;
		return res;
	}
	int sqrt(int n, int P) { // 开根号
		Cipo::n = n, Cipo::P = P;
		if (qpow(n, (P-1)>>1) == P-1) return -1; // n不是二次剩余
		while (a = rd() % P, qpow(t = (1ll*a*a-n+P)%P, (P-1)>>1) == 1); // 判断a^2-n得到的是不是二次剩余，如果是重新随机a
		return qpow((comp){a, 1}, (P+1)>>1).x; // 返回结果
	}
}

int main() {
	srand(time(0));
	T = read();
	while (T--) {
		N = read(), P = read(); N %= P;
		if (!N) { printf("0\n"); continue; } // 如果n=0表明x=0(%p)
		if (P == 2) { printf("1\n"); continue; } // p=2特判
		int ans = Cipo::sqrt(N, P); // 开根
		if (ans == -1) printf("Hola!\n"); // 无解
		else printf("%d %d\n", min(ans, P-ans), max(ans, P-ans)); // 否则有两解
	}
    return 0;
}

　　该算法的复杂度：\(\text{O}(\log p)\)。

　　附期望是\(2\)的证明：

\[\sum_{i=1}^{\infty}\frac{1}{2^i}\times i （这个由期望的定义来：概率×次数）\\
=\sum_{i=0}^{\infty}\frac{1}{2^i} + \frac{1}{2}\sum_{i=0}^{\infty}\frac{1}{2^i}+\dotsb - (1+\frac{1}{2}+\frac{1}{4}+\dotsb) \\
=2+1+\frac{1}{2}+\dotsb-2 \\
=2\times 2-2=2
\]

K次剩余

　　定义同上，只不过把\(2\)换成了\(k\)，但无法套用上面的解法求解。这里仍然假定\(p\)是奇质数。

　　发现构造走不通了！没关系，我们学习了原根！

　　众所周知原根遍历了所有与\(p\)互质的数，所以我们用原根替换它们。

　　比如说\(x^k \equiv a \pmod p\)，设\(g\)为原根，\(a=g^s\)，\(x=g^m\)，则原式变成了\((g^m)^k \equiv g^s \pmod p\)，也就是\(g^{km} \equiv g^s \pmod p\)，\(s\)可以通过\(\text{BSGS}\)解得；\(m\)未知。然后由阶的性质得到\(km \equiv s \pmod{\varphi(p)}\)，也就是\(km \equiv s \pmod{p-1}\)，解\(m\)即可。

　　想要所有解？刚刚的同余方程的解在模\(p-1\)的意义下的所有取值即为所有解。事实上题目一般要求找出任意解，正常解同余方程即可。如果上面的任意一步都出了问题（比如说\(s\)无解，或者同余方程没有解），那就没有解了。

// 码量惊人，博主写了140+行。这里只放最核心部分
// 这里用K次剩余解决二次剩余问题
int solve(int k, int a, int P) { // x^k=a (%p)
	int s = BSGS(g, a, P); // 找出s使得g^s=a
	int d = gcd(k, P-1);
	if (s == -1 || s % d) return -1; // BSGS无解或同余方程无解，说明该问题无解
	return qpow(g, 1ll*(s/d)*inv(k/d, (P-1)/d)%P, P); // 解同余方程km=s(%phi(p))
}

int main() {
	init(); // 初始化质数表

	T = read();
	while (T--) {
		N = read(), P = read(); N %= P;
		if (!N) { printf("0\n"); continue; }
		if (P == 2) { printf("1\n"); continue; }
		getG(P); // 得到模P的原根
		int ans = solve(2, N, P); // 解决K次剩余就写成solve(K, N, P)
		if (ans == -1) printf("Hola!\n");
		else printf("%d %d\n", min(ans, P-ans), max(ans, P-ans));
	}

	return 0;
}

Miller Rabin

　　如果我们想要快速判断一个数是不是质数，你可能会想到\(\text{O}(\sqrt n)\)复杂度的算法，但这个算法太劣了；或者想到运用费马小定理，因为当\(p\)为质数时有\(a^{p-1} \equiv 1 \pmod p\)，所以猜测逆命题也成立。我们通过随机\(a\)判断式子是否成立来判断\(p\)是不是质数。如果不准确，一次中了不代表一定是质数，那么我们多测几次，可以将其为合数的概率降到很低。但有一类特殊的合数能让式子恒成立，无论你怎么选择\(a\)，该同余式子一直成立，这类合数叫做\(\text{Carmichael}\)数，例如\(561\)。

　　那怎么办呢？先介绍一下二次探测原理。

　　若\(p\)是质数，且有\(a^2 \equiv 1 \pmod p\)，那么\(a \equiv \pm 1 \pmod p\)。前文有类似的证明，也就是移项化成整除式，这里就不证了。

　　我们通过这个方法来验证。

　　把\(p-1\)分解成\(2^k \times t\)。然后随机一个\(a\)然后让其自乘成\(a^2\)，结合二次探测原理来判断，如果在某一时刻自乘出\(1\)，则前一次必须是\(1\)或\(p-1\)，否则违背了原理，这个一定是合数。测试\(t\)轮后就得到了\(a^{p-1}=a^{2^k \times t}\)。如果最后得到的数不是\(1\)，那么就违背了费马小定理，\(p\)是合数。

　　据说测试\(n\)次的正确率为\(1-\left( \frac{1}{4} \right)^n\)。

int test[10] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29}; // 据说用这几个数在OI的ll范围内出错率为0%

int MR(ll P) {
    if (P == 1) return 0; // 毒瘤的1:他不是质数，但会卡后面
    ll t = P-1; int k = 0;
    while (!(t & 1)) k++, t >>= 1; // 分解出2
    rep(i, 0, 9) {
        if (P == test[i]) return 1; // test中的数都是质数。如果这个数出现过那它一定是质数
		else if (test[i] > P) return 0; // 测试的数比模数大，说明测试失败了
        ll a = pow(test[i], t, P), nxt = a; // 初始化a=test[i]^t%P
        rep(j, 1, k) {
            nxt = Mult(a, a, P); // 计算nxt=a^2%P。由于模数可能很大，这里的Mult用的是gui速乘
            if (nxt == 1 && a != P-1 && a != 1) return 0; // 如果违背了二次探测定理，测试失败
            a = nxt;
        }
        if (a != 1) return 0; // 违背了费马小定理，测试失败
    }
    return 1; // 通过了所有的测试
}

　　忽略快（gui）速乘的复杂度，该复杂度为\(\text{O}(\log P)\)。

Pollard Rho

　　\(\text{Pollard-Rho}\)是一个用来快速分解质因数的算法，它巧妙的运用了“生日悖论”这一现象将\(N\)分解，配合着\(\text{Miller-Rabin}\)可以将复杂度降为\(\text{O}(N^{\frac{1}{4}})\)。

　　描述这个算法，我们先从“生日悖论”说起。

　　班级里有\(50\)名学生，保证生日是随机的，不存在暗箱操作。假定一年为\(365\)天，问出现两个人生日相同的概率是多少？你可能脱口而出：\(\frac{50}{365}\)。

　　但事实上概率非常之高以至于几乎肯定有两个人的生日在同一天，这个概率\(P=1-\frac{365 \choose 50}{365^{50}} \approx 97.142\%\)。为啥直觉跟计算出来的差异如此之大？原因在于要保证两两生日都不等的概率占样本空间的比重非常之小。换个问题：如果你走进一个\(50\)人的班级里，你与班级里同学生日相等的概率又是多少呢？这时就是\(\frac{50}{365}\)了。

　　然后有一个结论：假设一年有\(N\)天，出现两个人生日在同一天的期望人数是\(\text{O}(\sqrt N)\)。这个证明博主不会，直接跳过。

　　进入到\(\text{Pollard-Rho}\)前，还要介绍一个算法中的一个随机函数。

　　设随机函数\(f(x)\)，在模\(P\)的意义下，满足\(f(x)=x^2+c\)，\(c\)为随机参数，那么构成了\([0,P)\rightarrow[0, P)\)下的映射，且有\(f(x)=f(x+P)\)。借助初始参数\(x_0\)构造随机数列\(\{ x_i\}\)，满足：\(\forall i>0 : x_i=f(x_{i-1})\)。显然其在模\(N\)意义下必定会走向一个循环，因为定义域和值域大小有限。这个函数生成的数列还是很随机的，然后根据根据生日悖论有期望环大小为\(\text{O}(\sqrt P)\)，原因是如果出现了之前出现过的数字，显然就会走入循环，根据上面的结论，出现两个相同数字的期望次数就为\(\text{O}(\sqrt P)\)。把\(x\)的一步一步映射画出来图，发现长得十分像\(\rho\)，算法由此得名。

　　对于将要被分解的数\(N\)，我们选取两个数字\(s\)和\(t\)，如果有\((\mid s-t \mid, N) \neq 1,N\)，很显然我们找到了一个因子，可以递归分解两部分了。但是毕竟数字太多，如何合理地随机\(s\)和\(t\)呢？就运用随机函数。

　　如果我们随机选取一些数字两两判断发现时间复杂度和空间复杂度又会弹回去。所以我们采用“\(\text{Floyd}\)判圈法”：有两个人在起点\(x_0\)处，在环上一个人一次走一步，另一个一次走两步。当他们再次相遇的时候表明一个人至少走完了一圈。这时一个人的数字记为\(s\)，另一个记为\(t\)，再继续如上判断。运用此方法能更好判环。

　　期望下我们需要\(\text{O}(N^{\frac{1}{4}})\)找出来一个因子。假设\(P\)可被分解，有\(P=a_1a_2,a_1 \leq a_2\)，在模\(P\)意义下，生成出来的序列出现环的期望为\(\text{O}(\sqrt N)\)。对于环上的任意两个数\(x'\)和\(x''\)，\((\mid x'-x'' \mid, P)=a_1\)，当且仅当：\(x' \equiv x'' \pmod {a_1}\)成立。而生成的数列\(\{x_i\}\)在模\(N\)下是随机的，在模\(a_1\)下也是随机的，再次运用结论得到出现\(x'\equiv x''\)的期望为\(\text{O}(\sqrt{a_1})\)，又因为有\(a_1 \leq \sqrt P\)，所以得到期望为\(\text{O}(N^{\frac{1}{4}})\)。

　　但是还有种情况：\(x'=x''\)，会导致\((\mid x' - x'' \mid, P)=P\)。这表明两个人相遇，选取的是环上的同一个数。遇到这种情况表明我们随机数选取的不好，要更换随机参数\(c\)重新操作。至此最原始的\(\text{Pollard-Rho}\)就出来了。

　　分析复杂度时我们只关心最大的数分解的复杂度，分解后的数字继续分解对总复杂度的贡献不大。但要不断求\(\gcd\)，总复杂度为\(\text{O}(N^{\frac{1}{4}}\log N)\)。有\(\log\)的复杂度不好看，考虑削掉。

　　为了减少\(\gcd\)的次数，我们将若干次得到的\(\mid s-t \mid\)的结果乘起来。\((a,b)=d\)时，\((ac \bmod b,b)\geq d\)一定成立。记乘积模\(N\)的值为\(prod\)，如果\((prod,N)=1\)，显然每一次\(\mid s-t \mid\)都与\(N\)互质；如果\(=N\)，表明其中必定有因子或\(0\)；否则就是\(N\)的因子。此时我们退回来一步一步判断，找出因子或者是发现相遇了。调整适当的次数连乘，均摊下来复杂度就变成了\(\text{O}(N^{\frac{1}{4}})\)。

// 下列程序段实现求N的最大质因子
inline ll f(ll x, ll c, ll p) { return inc(Mult(x, x, p), c, p); } // 随机函数

ll Floyd(ll N) {
	ll c = rand()&15, s = 1, t = f(s, c, N); // 随机c，s=1表示x0=1，t表示从起点跳一步
	for (;;) {
		ll _s = s, _t = t, prod = 1;
		for (int i = 1; i <= 128; i++)
			prod = Mult(prod, abs(_s - _t), N), _s = f(_s, c, N), _t = f(f(_t, c, N), c, N); // 连续处理128步
		ll d = gcd(prod, N); // d=(prod, N)
		if (d == 1) { s = _s, t = _t; continue; } // 如果d=1，表示没找到因子，再来一组
		for (int i = 1; i <= 128; i++) {
			if ((d = gcd(abs(s - t), N)) != 1) return d; // !=1返回
			s = f(s, c, N), t = f(f(t, c, N), c, N); // 否则继续
		}
	}
}

ll PR(ll N) { // Pollard-Rho主过程
	if (MR(N)) return N; // 如果N是质数，直接返回
	ll ans;
	while ((ans = Floyd(N)) == N); // 找到的是同一个点，重新来
	return max(PR(ans), PR(N / ans)); // 递归，返回最大值
}

int main() {
	srand(time(0));
	scanf("%d", &T);
	while (T--) {
		scanf("%lld", &N);
		ll ans = PR(N); // 找最大的质因子
		if (ans == N) printf("Prime\n"); else printf("%lld\n", ans);
	}
	return 0;
}

Möbius反演相关

　　博主曾经写过一篇，可能不够完整，在这里就放个链接了：Mobius反演学习

　　（准备填天坑）

前置知识

　　前文谈了很多关于数论的知识，这里加上一些严谨的定义。

　　数论函数：定义域为\(\Z\)，值域\(\subseteq \Complex\)的函数。多数情况下值域也为\(\Z\)。

　　积性函数：设\(f\)为数论函数，\(\forall a,b:(a,b)=1\)，有\(f(ab)=f(a)f(b)\)恒成立，则称\(f\)为积性函数。特殊的，\(\forall a,b\)，有\(f(ab)=f(a)f(b)\)，则称\(f\)为完全积性函数，注意此时没有互质的要求。

　　质因数分解：将任意正整数化成若干个质数的幂的乘积，也就是将\(n\)化成这样的形式：\(n=p_1^{\alpha_1}p_2^{\alpha_a}\dotsb p_s^{\alpha_s}\)。

　　根据以上三条，由于\(f(n)=f(p_1^{\alpha_1})f(p_2^{\alpha_2})\dotsb f(p_s^{\alpha_s})\)，我们可以用线性筛在\(\text{O}(n)\)的时间内求解前\(n\)个积性函数的值。

　　提到这里，我们引入几个常用的数论函数。

　　单位函数：\(\epsilon (n)=[n=1]=\begin{cases}1&n=1\\ 0&n\neq 1\end{cases}\)。\([\text{state}]\)表示\(\text{state}\)为真时结果为\(1\)，否则为\(0\)。是完全积性函数。

　　除数函数：\(\sigma_k(n)=\sum\limits_{d \mid n}d^k\)。\(k=0\)表示求其约数个数此时简写成\(d(n)\)；\(k=1\)表示求约数和，此时简写成\(\sigma(n)\)。不难证明，除数函数也是积性函数。

　　欧拉函数：就是前文讲的\(\varphi(n)\)，也是积性函数。欧拉函数有一个重要的性质：\(n=\sum\limits_{d \mid n}\varphi(d)\)。

　　\(Proof\)：

\[\sum_{d \mid n}\varphi(d) = \sum_{d \mid n}\varphi(\frac{n}{d})
\]

\[相当于把累加的顺序调换
\]

\[我们从新的角度理解右面的式子：\varphi(\frac{n}{d})表示与n的\gcd 为d的数的个数
\]

\[显然所有1到n都会对应到不同的d中，这个式子的总和就是n
\]

\[\sum_{d \mid n}\varphi(\frac{n}{d})=\sum_{d \mid n} \sum_{d \mid i}[(n,i)==d]=\sum_{i=1}^n\sum_{d \mid i,d \mid n}[(n,i)==d]=n
\]

\[中间一步调换了求和顺序，这个在之后的证明很常用
\]

\[由于两个数的\gcd 唯一，所以后面的式子直接等于n，\text{Q.E.D}
\]

　　幂函数：\(\text{Id}_k(n)=n^k\)。这里是数论中的幂函数。\(k=1\)时可以省略。

　　理论基础貌似差不多了。

Dirichlet卷积

　　设\(f\)，\(g\)是数论函数，对于数论函数\(h\)如果\(\forall n\)，\(h(n)=\sum\limits_{d \mid n}f(d)g\left(\dfrac{n}{d}\right)\)或者\(h(n)=\sum\limits_{i\times j=n}f(i)g(j)\)（两式意义一样），称\(h\)为\(f\)和\(g\)的\(\text{Dirichlet}\)卷积，简记\(h=f*g\)。

　　\(\text{Dirichlet}\)卷积有以下性质。

　　交换律和结合律：\(f*g=g*f\)，\(f*(g*h)=(f*g)*h\)。这些直接拿定义证明即可。

　　\(f*\epsilon=f\)，即任何数论函数与单位函数的卷积为本身。

　　以及有非常重要的应用：\(\sigma_k(n)=\text{Id}_k * 1\)和\(Id=\varphi * 1\)。前面的是定义得来的，后面的是刚刚讲的证明，这些都是卷积形式。

Möbius反演

　　提到\(\text{Möbius}\)反演之前，需要了解\(\bold{Möbius}\)函数。

　　\(\bold{Möbius}\)函数：\(\mu(n)=\begin{cases} (-1)^s &n=p_1p_2\dotsb p_s,s可以为0，此时为1\\0 &\exist p_i: p_i^2 \mid n \end{cases}\)。这里\(p_i\)都是质数。\(\mu\)是积性函数，同样也可以用线性筛求解。

　　\(\mu\)有什么用？一个很重要的性质：\(\mu * 1 = \epsilon\)。

　　\(Proof\)：

\[(\mu * 1)(n) = \sum_{d \mid n}\mu(d)
\]

\[当n=1时，(\mu *1)(1)=\mu(1)=1=\epsilon(1)
\]

\[当n>1时，仍然从别的角度来理解
\]

\[只有当d=p_1p_2\dotsb p_s时\mu(d) \neq 0，反之若存在相同质因子，\mu(d)=0
\]

\[假设n含有s个质因子，每个因子只能选0个或1个，且相互独立
\]

\[\therefore \sum_{d \mid n}\mu(d)=\sum_{i=0}^s(-1)^i{s \choose i}=(1-1)^s=0
\]

\[而\epsilon(n)=0，即证\mu*1=\epsilon
\]

　　然后定义\(\text{Möbius}\)变换：如果\(g=f*1\)，则称\(g\)为\(f\)的\(\text{Möbius}\)变换，而\(f\)为\(g\)的\(\text{Möbius}\)逆变换。往往我们想运用逆变换，此时称作\(\text{Möbius}\)反演。此时有：

\[f=g*\mu
\]

　　\(Proof\)：

\[很简单却很重要，直接用\text{Dirichlet}卷积证
\]

\[\because g=f*1
\]

\[\therefore g*\mu=f*1*\mu=f*(1*\mu)=f*\epsilon=f
\]

\[\text{Q.E.D}
\]

　　该定理称为\(\bold{Möbius}\)反演定理。

数论函数筛法

泰勒公式

　　给一个函数\(f(x)\)和其在\(x_0\)处的取值，用下面的式子无限逼近\(f(x)\)：

\[f(x)=f(x_0)+\frac{f'(x_0)}{1!}(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+\dotsb
\]

　　相当于通过数学的手段不断拟合。怎么拟合？

　　下文的定义可能不那么严谨，不影响后文应用。

　　拉格朗日中值定理：

\[给定区间[a,b]，至少有一点\varepsilon (a<\varepsilon<b)，使得f(b)-f(a)=f'(\varepsilon)(b-a)成立
\]

　　这个定理很显然，随便证。（原命题好像更严谨，这里不会影响下文）

　　于是又有了有限增量定理：

\[\lim_{\Delta x\rightarrow 0}(f(x_0+\Delta x)-f(x_0))=f'(x_0+\theta \Delta x)\Delta x,0 < \theta < 1
\]

　　所以我们有：

\[f(x)-f(x_0)=f'(x_0)(x-x_0)+a \Rightarrow f(x) = f(x_0)+f'(x_0)(x-x_0)+a
\]

　　但是当\(\Delta x\)很大时往往\(a\)的影响会变大，我们需要更进一步。

　　考虑构造一个多项式：

\[P(x)=A_0+A_1(x-x_0)+A_2(x-x_0)^2+A_3(x-x_0)^3+\dotsb
\]

　　我们不断向函数\(f(x)\)拟合，也就是让：

\[P(x_0)=f(x_0)
\]

\[P'(x_0)=f'(x_0)
\]

\[P''(x_0)=f''(x_0)
\]

\[\dotsb
\]

\[P^{(n)}(x_0)=f^{(n)}(x_0)
\]

　　所以有：

\[P(x_0)=A(x_0)
\]

\[P'(x_0)=1!A'(x_0)
\]

\[P''(x_0)=2!A''(x_0)
\]

\[\dotsb
\]

\[P^{(n)}(x_0)=n!A^{(n)}(x_0)
\]

　　得到表达式：

\[P(x)=f(x_0)+\frac{f'(x_0)}{1!}(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+\dotsb+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n
\]

　　然后还有个误差分析关于\(f(x)-P(x)\)。感觉有点超其实我不会所以就不管了。最后得到的误差很小小于我们定的阶数\(n\)，所以在\(n\)趋于\(+\infin\)下，命题成立。

　　运用这个公式的例子：

\[e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\dotsb
\]

\[\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dotsb
\]

\[\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\dotsb
\]

多项式

　　多项式\(A(x)=a_0+a_1x+a_2x^2+\dotsb\)在平常十分常见，其应用十分广泛，如多项式乘法、生成函数等等。多项式与多项式之间可以运算。多项式的度数即为最高项的次数，记作\(\text{deg}_A\)。对于\(A(x)=\sum_{i=0}^n a_ix^i,a_n\neq 0\)有时直接称\(A(x)\)为\(n\)次多项式

　　有两个多项式\(A,B\)，定义多项式加法：\(A(x)+B(x)=\sum_{i=0}^{\max(\deg_A,\deg_B)}(A_i+B_i)x^i\)；

　　定义多项式乘法：\(A(x)B(x)=\sum_{i=0}^{\deg_A} \sum_{j=0}^{\deg_B} A_iB_jx^{i+j}=\sum_{i=0}^{\deg_A+\deg_B} \sum_{j+k=i}A_jB_kx^{j+k}\)。后面的变形在之后应用上会比较方便。

　　观察发现多项式加法的复杂度为\(\text{O}(n)\)，乘法为\(\text{O}(n^2)\)。乘法的复杂度过高了，有没有办法让复杂度降下来呢？

　　我们平常所采用的多项式表示方法为系数表示法。此外，还有点值表示法，由于有一个定理：\(n\)个点唯一确定最高次数为\(n-1\)的多项式。我们就用\(n+1\)个点表示一个\(n\)次多项式。也就是说对于一个n次多项式\(A(x)\)，找一组数\(\{x_0, x_1,\dotsb, x_n\}\)，用\(n+1\)个点\((x_0,A(x_0))\)、\((x_1,A(x_1))\dotsb(x_n,A(x_n))\)。采用这个方式有什么好处呢？对于多项式加法\(A(x)+B(x)\)，假定次数都为\(n\)，那么得到的\(n+1\)个点即为\((x_i,A(x_i)+B(x_i)),i\in [0,n]\)；同理对于多项式乘法\(A(x)B(x)\)，得到的\(n+1\)个点即为\((x_i,A(x_i)B(x_i))\)。这样操作一次的复杂度为\(\text{O}(n)\)了，优点就在此。

　　但是我们还面临着问题：就是系数表示和点值表示之间如何转换？系数向点值的转化很简单，用一下秦九韶公式（自行翻阅数学必修三），这需要\(\text{O}(n^2)\)的复杂度；而点值向系数需要用到拉格朗日插值，同样也需要\(\text{O}(n^2)\)。可是这样的复杂度并不优秀，如果我们采用转换表示方法的角度来加快运算，虽然运算的复杂度降低，但是转换的复杂度仍然很高，即使我们采用后文的快速变换改进公式也不够优秀，这样似乎变得不可行，其实之后我们会使用一组特殊的点使得转换的速度加快。对于一般的点而言只能运用拉格朗日插值还原成系数表示，下面先介绍这个方法。

拉格朗日插值

　　给你\(n\)个点\((x_i,y_i)\)（保证\(x\)互不相同），这样能确定一个多项式\(f(x)\)。给你\(x\)，求出\(f(x)\)。该算法解决这样的问题。

　　用中学的知识考虑：对于\(1\)个点，确定一条水平的线；对于\(2\)个点，可以解出一条直线。对于\(3\)个点，可以解出一条抛物线。但是随着点数的增多，我们需要求解一个\(n+1\)元一次方程，而解方程要用到高斯消元（后文会提到），这个的复杂度是\(\text{O}(n^3)\)，不够优秀。下面我们有巧妙的方法来构造使得复杂度为\(\text{O}(n^2)\)，加上多项式快速变换可以在\(\text{O}(n \log^2 n)\)的时间内还原出多项式，但这个的基础就是要用到拉格朗日插值。

　　构造函数\(l_i(x)=\prod_{j \neq i}\frac{x-x_j}{x_i-x_j}\)。这样有什么好处呢？当\(x=x_j,j=1,2 \dotsb,j \neq i\)时，\(l_i(x)=0\)；反之如果\(x=x_i\)，\(l_i(x)=1\)。

　　构造多项式\(f(x)=\sum_{i=1}^n y_i l_i(x)\)，则这个多项式就是我们要求的多项式。往往只要求其中一个点时的值，就把\(x\)代入求解，毕竟直接还原多项式复杂度比较高。

　　这为什么是对的？由于构造的函数一定经过这\(n\)个点，而且保证过\(n\)个点一定确定小于\(n\)次的多项式，而这个就是我们要的多项式。

　　最终式子：

\[f(x)=\sum_{i=1}^n y_i \prod_{j \neq i}\frac{x-x_j}{x_i-x_j}
\]

　　求解这个式子的复杂度为\(\text{O}(n^2)\)。

	for (int i = 1; i <= n; i++) {
		int mul = y[i], div = 1; // mul表示y[i]和式子分母的乘积
		for (int j = 1; j <= n; j++)
			if (i != j) mul = 1ll*mul*dec(k, x[j])%P, div = 1ll*div*dec(x[i], x[j])%P; // 分母分子分别乘上对应的数
		ans = (ans + 1ll*mul*qpow(div, P-2)) % P; // 算到ans中
	}

　　优化在后面会见到。

快速傅里叶变换(FFT)

　　快速在哪呢？转换的过程只需要\(\text{O}(n \log n)\)，也就是说多项式乘法的复杂度就会降至\(\text{O}(n \log n)\)。\(\text{FFT}\)分为\(\text{DFT}\)和\(\text{IDFT}\)，分别称作离散傅里叶变换和逆离散傅里叶变换，这些变换是时域与频域之间的转换，不过我们并不关心。学习该算法前我们需要学习复数的相关知识。

复数

　　复数是为了完善数学体系而新增加的一类数，用\(\Complex\)表示这类数的集合。具体来说，引入了\(i=\sqrt{-1}\)，于是所有复数都可以写成\(z=a+bi\)这种形式，其中\(a,b\in \R\)，\(a\)被称作实部，\(b\)被称作虚部。特殊的，当\(b=0\)时这类数称为实数；当\(a=0\)时这类数称为纯虚数。

　　复数可以对应成向量。

　　首先复数有一些基本定义和运算：

　　对于复数\(z=a+bi\)，

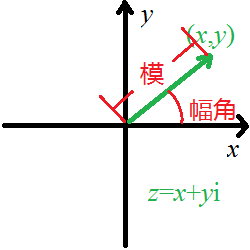
　　定义复数的模\(\mid z \mid=\sqrt{a^2+b^2}\)。这个运用勾股定理即可得出。

　　定义复数的幅角：\(z\)在平面上对应的点与原点的连线上，如果\(x\)的正半轴逆时针旋转\(\theta\)角度与连线重合，则模角为\(\theta\)。注意是逆时针方向，不能从顺时针方向。

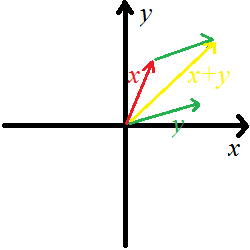
　　定义两个复数\(x=a_x+b_xi\)，\(y=a_y+b_yi\)，复数的加法\(x+y=(a_x+a_y)+(b_x+b_y)i\)；减法同理。几何意义就是向量的加减，遵循平行四边形法则。

　　定义复数的乘法：\(xy=(a_xa_y-b_xb_y)+(a_xb_y+a_yb_x)i\)。推导运用上文对\(i\)的定义即可（\(i^2=-1\)）。除法类似，对下文不重要便略去。复数乘法在几何上的意义非常有趣且很特别：对于乘出来的复数，其模为两个乘数的模相乘，其幅角等于两个乘数的幅角相加。

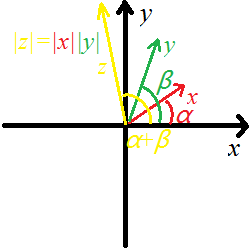
　　证明可以运用三角变换。同时我们得到了\(\mid z \mid = \mid x \mid \mid y \mid\)。

　　定义共轭复数\(\overline z\)表示与\(z\)实部相等，虚部相反，即\(\overline z=a-bi\)。有一个推导公式\(\overline{ab}=\overline a \cdot \overline b\)，据说这个公式能够优化掉\(\text{FFT}\)的\(\frac{1}{2}\)的常数，博主不会。几何意义是两个复数乘法前后在平面上关于\(x\)轴对称。

　　欧拉公式：\(e^{i\theta}=\cos \theta + i\sin \theta\)。证明要用到泰勒公式，直接展开即可。这个代数写法能很大程度代替几何上的描述。比如复数乘法就可以转化成指数上角的相加了。这个公式很重要，后文将会用到。

　　由以上的知识我们可以进入\(\text{FFT}\)的学习了。

正文：DFT、IDFT和优化

DFT

　　\(\text{DFT}\)实现的是将系数表达转变成点值表达，对于一个次数小于\(2^n\)的多项式，我们选择特殊的\(2^n\)个点使得转换的速度加快。

　　首先定义单位根\(\omega_n=e^{\frac{2\pi i}{n}}\)，其中\(n\)是\(2\)的幂。后文中默认\(n\)都为\(2\)的幂次，包括实现。相当于将\(1\)沿逆时针方向旋转\(\frac{2\pi}{n}\)的弧度。假设\(n=8\)，如下图。

　　其模为\(1\)，幅角为\(45^\circ\)。对于其的任意次幂如下。

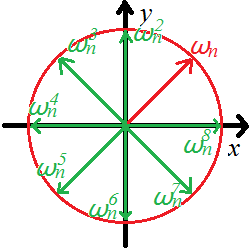
　　实际上这个是\(x^n=1\)的所有解。

　　发现\(\omega_n\)到\(\omega_n^n\)八个复数正好平分了半径为\(1\)的单位圆，且有\(\omega_n^k=\omega_n^{k \bmod n}\)。特别的，\(\omega_n^{kn}=\omega_n^0=1\)。

　　对于一个多项式\(A(x)\)，我们希望快速求出\(A(\omega_n^0)\)、\(A(\omega_n^1)\)、\(A(\omega_n^2)\dotsb A(\omega_n^{n-1})\)的值，这些共能组成\(n\)个点。

　　接着介绍几个有用的定理。这些可以直接运用定义证明。

　　定理\(1\)：\(\omega_{dn}^{dk}=\omega_n^k\)。（消去引理）

　　\(Proof\)：

\[\omega_{dn}^{dk}=e^{\frac{2dk\pi i}{dn}}=e^{\frac{2k\pi i}{n}}=\omega_n^k
\]

　　定理\(2\)：\((\omega_{n}^k)^2=(\omega_n^{k+n/2})^2\)。（折半引理）

　　\(Proof\)：

\[(\omega_n^k)^2=\omega_n^{2k}=\omega_n^{2k}\omega_n^n=\omega_n^{2k+n}=(\omega_n^{k+n/2})^2
\]

　　这个引理非常重要。

　　定理\(3\)：\(\sum_{i=0}^{n-1}\omega_n^i=0\)。（求和引理）

　　\(Proof\)：

\[由于n>1，一定有\omega_n-1\neq 0，直接用等比数列公式：\sum_{i=0}^{n-1}\omega_n^i=\frac{\omega_n^n-1}{\omega_n-1}=\frac{1-1}{\omega_n-1}=0
\]

　　这个在\(\text{IDFT}\)中会用到。

　　有了上面的东西，我们就可以考虑对多项式进行变形而运用分治求解。

　　对于一个多项式\(A(x)=\sum_{i=0}^{n-1}a_ix^i\)，按照\(i\)的奇偶分成两组得到：

\[A(x)=\sum_{i=0}^{n/2-1}a_{2i}x^{2i}+\sum_{i=0}^{n/2-1}a_{2i+1}x^{2i+1}=\sum_{i=0}^{n/2-1}a_{2i}(x^2)^i+x\sum_{i=0}^{n/2-1}a_{2i+1}(x^2)^i
\]

　　然后假设：

\[A^{[0]}(x)=\sum_{i=0}^{n/2-1}a_{2i}x^i
\]

\[A^{[1]}(x)=\sum_{i=0}^{n/2-1}a_{2i+1}x^i
\]

　　所以我们有：

\[A(x)=A^{[0]}(x^2)+xA^{[1]}(x^2)
\]

　　这样我们可以运用以上引理了。

　　\(A(x)\)在\(\omega_n^k\)和\(\omega_n^{k+n/2}\)处的取值：

\[A(\omega_n^k)=A^{[0]}((\omega_n^k)^2)+\omega_n^kA^{[1]}((\omega_n^k)^2)=A^{[0]}(\omega_{n/2}^k)+\omega_n^kA^{[1]}(\omega_{n/2}^k)
\]

\[A(\omega_n^{k+n/2})=A^{[0]}((\omega_n^{k+n/2})^2)+\omega_n^{k+n/2}A^{[1]}((\omega_n^{k+n/2})^2)
\]

　　因为折半引理和消去引理，\(\omega_n^k = -\omega_n^{k+n/2}\)，所以有：

\[A(\omega_n^{k+n/2})=A^{[0]}(\omega_{n/2}^k)-\omega_n^kA^{[1]}(\omega_{n/2}^k)
\]

　　这样我们可以通过求出\(A^{[0]}(\omega_{n/2}^k)\)和\(A^{[1]}(\omega_{n/2}^k)\)来求出\(A(\omega_n^k)\)和\(A(\omega_n^{k+n/2})\)。而对于每一个长度为\(n\)的多项式，我们在递归后都需要\(\text{O}(n)\)的时间合并这一层的信息，所以总复杂度就是\(\text{T}(n)=2\text{T}(\frac{n}{2})+\text{O}(n)=\text{O}(n \log n)\)了。

// 代码有些难懂，需要细细体会
void DFT(comp *a, int l, int r) { // 长度一定要为2的幂
	if (l == r) return; // 区间只有一个元素退出
	int mid = l+r>>1, len = mid-l+1; // mid表示区间中点，len表示每组的长度，对应了n/2
	static comp t[maxn << 2]; // 用来存交换的东西
	for (int i = 0; i < len<<1; i += 2) t[l+(i>>1)] = a[l+i]; // 按照奇偶分组。先是偶数放前面
	for (int i = 1; i < len<<1; i += 2) t[l+len+(i>>1)] = a[l+i]; // 再是奇数
	for (int i = l; i <= r; i++) a[i] = t[i]; // 拷贝回去
	DFT(a, l, mid), DFT(a, mid+1, r); // 先递归算出左右区间的插值结果
	comp Wn = (comp){cos(PI/len), sin(PI/len)}, W = (comp){1, 0}; // 计算单位根Wn，单位根的幂用W表示
	for (int i = 0; i < len; i++)
		t[l+i] = a[l+i] + W*a[l+len+i], t[l+len+i] = a[l+i] - W*a[l+len+i], W = W * Wn; // 算出l+i，l+len+i处的插值结果，对应的幂为i。
	for (int i = l; i <= r; i++) a[i] = t[i]; // 将算出的插值结果复制替换系数
}

IDFT

　　\(\text{IDFT}\)是将点值表达转成系数表达。先给出如下的定义。

　　定义\(M=\left[\begin{matrix}\omega_n^0 & \omega_n^0 & \omega_n^0 & \dotsb & \omega_n^0 \\ \omega_n^0 & \omega_n^1 & \omega_n^2 & \dotsb & \omega_n^{n-1} \\ \omega_n^0 & \omega_n^2 & \omega_n^4 & \dotsb & \omega_n^{n-2} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \omega_n^0 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \dotsb & \omega_n^1 \end{matrix}\right]\)，定义向量矩阵\(x=\left[\begin{matrix}a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_n \end{matrix}\right]\)，则\(\text{DFT}\)的作用就是求出\(y=Mx\)，而\(\text{IDFT}\)的作用就是利用\(y\)反求\(x\)。

　　仍然定义\(\overline{M}\)，\(\overline M_{ij}=\overline{M_{ij}}\)，表示\(\overline M_{ij}\)为对应的\(M_{ij}\)的共轭复数。

　　定理：\(\frac{1}{n}\overline My=x\)。

　　\(Proof\)：

\[观察发现：\overline M_{ij}=\omega_n^{-(i-1)(j-1)}，M_{ij}=\omega_n^{(i-1)(j-1)}
\]

\[对于矩阵\overline My=\overline MMx，记L=\overline{M}M，我们看L会得到什么
\]

\[L_{ij}=\sum_{k=1}^n \overline M_{ik}M_{kj}=\sum_{k=1}^n \omega_n^{-(i-1)(k-1)}\omega_n^{(k-1)(j-1)}=\sum_{k=1}^n\omega_n^{(k-1)(j-i)}=\sum_{k=0}^{n-1}(\omega_n^{j-i})^k
\]

\[此时我们应分类讨论
\]

\[当i=j时，\omega_n^{j-i}=1，上式=n
\]

\[当i\neq j时，\omega_n^{j-i} \neq 1，由求和引理得到上式=0
\]

\[也就是说L=\left[ \begin{matrix} n & 0 & \dotsb & 0 \\ 0 & n & \dotsb & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dotsb & n \end{matrix} \right]，正好等于nI
\]

\[\therefore \frac{1}{n}xL=x，利用这个即可证明定理
\]

void IDFT(comp *a, int l, int r) { // 跟DFT差不多
	if (l == r) return;
	int mid = l+r>>1, len = mid-l+1;
	static comp t[maxn << 2];
	for (int i = 0; i < len<<1; i += 2) t[l+(i>>1)] = a[l+i];
	for (int i = 1; i < len<<1; i += 2) t[l+len+(i>>1)] = a[l+i];
	for (int i = l; i <= r; i++) a[i] = t[i];
	IDFT(a, l, mid), IDFT(a, mid+1, r);
	comp Wn = (comp){cos(PI/len), -sin(PI/len)}, W = (comp){1, 0}; // 与上面的不同之处在于虚部有负号
	for (int i = 0; i < len; i++)
		t[l+i] = a[l+i] + W*a[l+len+i], t[l+len+i] = a[l+i] - W*a[l+len+i], W = W * Wn;
	for (int i = l; i <= r; i++) a[i] = t[i];
}
...
    for (int i = 0; i < N; i++) a[i].x /= N, a[i].y /= N; // 这句话把n除掉，要写在外面
...

FFT的改进

　　\(\text{FFT}\)的核心上文已经阐述完了，但是发现这样递归下来空间消耗很大，常数很大，因此我们需要优化。

　　首先发现\(\text{DFT}\)和\(\text{IDFT}\)几乎没有什么代码上的差别，我们可以合并。

　　然后将递归写法改成非递归写法。可是我们发现输入按单位根的幂是奇数还是偶数来分开算，从二进制上看，发现是最后一位是\(0\)的分一组，最后是\(1\)的分一组。接着考虑倒数第二位，继续如上操作。当\(n=8\)，分组如下。

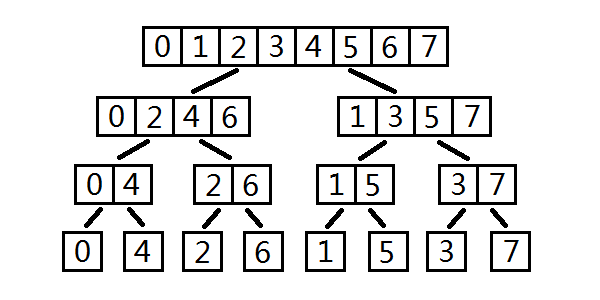
　　最下面一层顺序是\(\{0,4,2,6,1,5,3,7\}\)，做\(\text{FFT}\)的过程中每层连续两组合并起来，每组越合并越大，合并是将两组的数从左往右每次取出一个排成的。第一层的单位根为\(\omega_8\)，第二层是\(\omega_4\)，第三层是\(\omega_2\)，而每组对应的都是\(A(x)\)在\(\omega_n^0\)到\(\omega_n^{n-1}\)处的取值，这样一来计算就可以从底往上合并了。

　　但是如何得到最底下一层的顺序呢？

　　把最底下一层二进制写出来：\(\{000,100,010,110,001,101,011,111\}\)，再把下标\(0\)到\(7\)的二进制列出来：\(\{000,001,010,011,100,101,110,111\}\)。发现正好是将下标的二进制翻过来得到的序列！这个证明很简单，显然会先根据二进制末尾分组，然后再根据倒数第二位分组，以此类推，相当于下标的反串排序然后再翻过来，其实等于直接把下标翻过来（下标的反串构成的集合等于下标的集合）。

　　这样就能改进\(\text{FFT}\)了。具体细节看代码。

void FFT(comp *a, int n, int opt) { // n为长度，opt表示是DFT(1)还是IDFT(-1)
	static int rev[maxn << 2];
	for (int i = 0; i < n; i++)
		if ((rev[i] = rev[i>>1]>>1|(i&1?n>>1:0)) > i) swap(a[i], a[rev[i]]); // 细细品味线性递推出下标i对应的位置，通过二进制翻转求得
	for (int q = 1; q < n; q <<= 1) { // 考虑组的大小，从下往上合并
		comp Wn = (comp){cos(PI/q), opt*sin(PI/q)}; // 处理单位根，opt=1和-1时不一样
		for (int p = 0; p < n; p += q<<1) {
			comp W = (comp){1, 0}; // 单位根的幂
			for (int i = 0; i < q; i++) {
				comp tmp = a[p+q+i]*W; // 用tmp记录可以无需原来的t数组，这个是蝴蝶操作，用来优化。
				a[p+q+i] = a[p+i] - tmp;
				a[p+i] = a[p+i] + tmp;
				W = W * Wn;
			}
		}
	}
	if (opt == -1) for (int i = 0; i < n; i++) a[i].x /= n, a[i].y /= n; // 如果是IDFT要除n
}
// FFT(a, n, 1) 表示DFT
// FFT(a, n, -1) 表示IDFT

总结

　　\(\text{FFT}\)不仅仅能做多项式乘法，事实上，它以及后面的一系列变换都有一套模型：处理卷积问题。

　　定义运算\(\circ\)，则卷积为\(F_n=\sum_{i\circ j=n}a_ib_j\)，这些运算可以在\(\text{O}(n\log n)\)的时间求出\(F_0\dotsb F_{n-1}\)。在上面的问题中，运算符为\(+\)，多项式乘法就变成了求解\(F\)数组了。\(\text{diricklet}\)卷积对应运算符是\(\times\)。

拓展：分治FFT

　　（占坑）

// 洛谷P4721 【模板】分治 FFT
// 采用cdq分治解决，亦可采用多项式求逆
// 这个的核心思想就是求f[l,r]，在完成f[l,mid]的基础上，将f[l,mid]对f[mid+1,r]的贡献用fft扫出来，然后递归求解[mid+1,r]，此时一定有f[mid+1]解决。
// 前置知识：NTT
void divide(int l, int r) {
	if (l == r) return;
	int mid = l+r>>1;
	divide(l, mid); // 先完成f[l,mid]

	int len = r-l+1, N = 1;
	while (N < len) N <<= 1;
	memcpy(x, f+l, sizeof(int)*len); // 将f[l,r]拷到x
	memcpy(y, g, sizeof(int)*len); // 将g[0,len]拷到y
	for (int i = mid-l+1; i < N; i++) x[i] = 0; // 防止不必要的影响，将一些位置设成0
	fft(x, N, 1), fft(y, N, 1);
	for (int i = 0; i < N; i++) x[i] = 1ll*x[i]*y[i]%P; // 卷积
	fft(x, N, -1);
	for (int i = mid-l+1; i <= r-l; i++) f[l+i] = inc(f[l+i], x[i]); // 让f[mid+1,r]加上f[l,mid]对它们的贡献

	divide(mid+1, r); // 再完成f[mid+1,r]
}

　　复杂度：\(\text{O}(n \log^2 n)\)。运用生成函数加上多项式求逆可以做到\(\text{O}(n \log n)\)。

快速数论变换(NTT)

　　就是将多项式乘法限制在模意义下，通常模数都是\(\text{NTT}\)模数，即形如\(P=s\times 2^k+1\)的数，首先这个数必须是质数，其次要满足\(k\)尽量大，为什么呢？下面细细说来。

　　\(\text{NTT}\)与\(\text{FFT}\)十分相像：它也有单位根。单位根要满足其\(n\)次幂为\(1\)，小于\(n\)次都不为\(1\)，而原根能很好地胜任，因为有\(g^{\varphi(P)}=1\)且幂为任意\(\varphi(P)\)的因子都不为\(1\)。\(P\)是质数，所以\(\varphi(P)=P-1\)。我们可以构造\(\omega_n=g^{\frac{P-1}{n}}\)，这样\(\omega_n^n\equiv 1\)而且\(m<n,\omega_n^m \not\equiv 1\)。这样就可以完全替换掉\(\text{FFT}\)里面的东西了。由于\(n\)是\(2\)的幂且可能很大，所以对\(P-1\)的要求就是有很多的因子\(2\)。

　　\(\text{NTT}\)的优点在于：能在特定模数意义下运算、没有任何的精度丢失。但无法直接运用到任意模数\(\text{MTT}\)上。这样的情况后面再讨论。

　　代码如下。

// 这里NTT模数P取的是998244353，g=3。当然也可以取别的合适的
void NTT(int *a, int n, int opt) {
	static int rev[maxn << 2];
	for (int i = 0; i < n; i++)
		if ((rev[i] = rev[i>>1]>>1|(i&1?n>>1:0)) > i) swap(a[i], a[rev[i]]);
	for (int q = 1; q < n; q <<= 1) {
		int Wn = qpow(g, (P-1)/q>>1); // 这里用原根替换了复数
		if (opt == -1) Wn = qpow(Wn, P-2); // 如果是DFT，要求g^(-(P-1)/2)，实际上就是求上面那个数的逆元
		for (int p = 0; p < n; p += q<<1) {
			int W = 1;
			for (int i = 0; i < q; i++) {
				int tmp = 1ll*a[p+q+i]*W%P;
				a[p+q+i] = inc(a[p+i], P-tmp);
				a[p+i] = inc(a[p+i], tmp);
				W = 1ll*W*Wn%P;
			}
		}
	}
	if (opt == -1) for (int i = 0, inv = qpow(n, P-2); i < n; i++) a[i] = 1ll*a[i]*inv%P; // 这里除n变成乘逆元
}

　　常数也不小（主要是取模），但比\(\text{FFT}\)小。

快速沃尔什变换(FWT)

任意模数NTT(MTT)

　　具体原理详见myy的集训队论文。（先咕了~）

#include <bits/stdc++.h>

#define rep(i, a, b) for (int i = a, i##end = b; i <= i##end; ++i)
#define per(i, a, b) for (int i = a, i##end = b; i >= i##end; --i)
#define rep0(i, a) for (int i = 0, i##end = a; i < i##end; ++i)
#define per0(i, a) for (int i = a-1; ~i; --i)
#define chkmin(a, b) a = std::min(a, b)
#define chkmax(a, b) a = std::max(a, b)

typedef long long ll;

const int maxn = 100000 + 5;
const double PI = acos(-1);

int P;

inline int read() {
	int w = 0, f = 1; char c;
	while (!isdigit(c = getchar())) c == '-' && (f = -1);
	while (isdigit(c)) w = w*10+(c^48), c = getchar();
	return w * f;
}

struct comp {
	double x, y;
	comp(double x=0, double y=0) : x(x), y(y) {}
};
comp operator + (comp a, comp b) { return comp(a.x+b.x, a.y+b.y); }
comp operator - (comp a, comp b) { return comp(a.x-b.x, a.y-b.y); }
comp operator * (comp a, comp b) { return comp(a.x*b.x-a.y*b.y, a.x*b.y+a.y*b.x); }
comp conj(comp a) { return comp(a.x, -a.y); }

comp W[maxn << 2];
void prework(int n) {
	for (int i = 1; i < n; i <<= 1)
		for (int j = 0; j < i; j++) W[i+j] = comp(cos(j*PI/i), sin(j*PI/i));
}

void fft(comp *a, int n, int opt) {
	static int rev[maxn << 2] = {0};
	for (int i = 1; i < n; i++)
		if ((rev[i] = rev[i>>1]>>1|(i&1?n>>1:0)) > i) std::swap(a[i], a[rev[i]]);
	for (int q = 1; q < n; q <<= 1)
		for (int p = 0; p < n; p += q<<1)
			for (int i = 0; i < q; i++) {
				comp t = a[p+q+i]*W[q+i]; a[p+q+i] = a[p+i]-t, a[p+i] = a[p+i]+t;
			}
	if (~opt) return;
	for (int i = 0; i < n; i++) a[i].x /= n, a[i].y /= n;
	std::reverse(a+1, a+n);
}

void conv(int *x, int *y, int *z, int n) {
	for (int i = 0; i < n; i++) x[i] %= P, y[i] %= P;
	static comp a[maxn << 2], b[maxn << 2];
	static comp dfta[maxn << 2], dftb[maxn << 2], dftc[maxn << 2], dftd[maxn << 2];
	for (int i = 0; i < n; i++)
		a[i] = comp(x[i] >> 15, x[i] & 32767), b[i] = comp(y[i] >> 15, y[i] & 32767);
	fft(a, n, 1), fft(b, n, 1);
	for (int i = 0; i < n; i++) {
		int j = (n-i) & (n-1);
		static comp a1, a2, b1, b2;
		a1 = (a[i] + conj(a[j])) * comp(0.5, 0);
		a2 = (a[i] - conj(a[j])) * comp(0, -0.5);
		b1 = (b[i] + conj(b[j])) * comp(0.5, 0);
		b2 = (b[i] - conj(b[j])) * comp(0, -0.5);
		dfta[i] = a1 * b1, dftb[i] = a1 * b2, dftc[i] = a2 * b1, dftd[i] = a2 * b2;
	}
	for (int i = 0; i < n; i++)
		a[i] = dfta[i] + dftb[i] * comp(0, 1), b[i] = dftc[i] + dftd[i] * comp(0, 1);
	fft(a, n, -1), fft(b, n, -1);
	for (int i = 0; i < n; i++) {
		int ax = (ll)(a[i].x + 0.5) % P, ay = (ll)(a[i].y + 0.5) % P, bx = (ll)(b[i].x + 0.5) % P, by = (ll)(b[i].y + 0.5) % P;
		z[i] = (((ll)ax << 30) + ((ll)(ay + bx) << 15) + by) % P;
	}
}

int getsz(int n) { int x = 1; while (x < n) x <<= 1; return x; }

int n, m, N, a[maxn << 2], b[maxn << 2], c[maxn << 2];

int main() {
	n = read() + 1, m = read() + 1, P = read();
	rep0(i, n) a[i] = read();
	rep0(i, m) b[i] = read();
	N = getsz(n+m-1); prework(N);
	conv(a, b, c, N);
	rep0(i, n+m-1) printf("%d ", c[i]);
	return 0;
}

多项式基本操作

多项式求逆

　　给一个长度为\(n\)的多项式\(A\)（无关时\((x)\)略去），求\(B\)，满足\(AB\equiv 1 \pmod {x^n}\)。\(n\)不一定是2的幂。

　　求解需要用倍增的方法。注意下文模数的变化。

　　首先我们有：

\[AB \equiv 1 \pmod{x^n} \Rightarrow AB \equiv 1 \pmod{x^{\lceil \frac{n}{2} \rceil}}
\]

　　接着考虑构造一个解\(B'\)满足：

\[AB' \equiv 1 \pmod{x^{\lceil \frac{n}{2} \rceil}}
\]

　　所以有：

\[B \equiv B' \pmod{x^{\lceil \frac{n}{2} \rceil}} \Rightarrow B - B' \equiv 0 \pmod {x^{\lceil \frac{n}{2} \rceil}}
\]

　　两边同时平方得：

\[(B-B')^2 \equiv 0 \pmod{x^n}
\]

　　这里模数能平方是因为同余\(0\)，否则不可以直接平方。

　　展开：

\[B^2-2BB'+B'^2 \equiv 0 \pmod{x^n}
\]

\[AB^2-2ABB'+AB'^2 \equiv 0 \pmod{x^n} \Rightarrow B-2B'+AB'^2 \equiv 0 \pmod{x^n}
\]

　　所以我们就有：

\[B\equiv 2B'-AB'^2 \pmod{x^n}
\]

　　这样不断递归下去，当\(n=1\)时就是\(A\)常数项的逆元。在此基础上倍增构造即可。复杂度\(\text{O}(n \log n)\)。

// 多项式以及一些支持的操作
struct poly {
	int a[maxn << 1], len; // 各项系数和长度
	poly(int a0=0) : len(1) { memset(a, 0, sizeof a); a[0] = a0; } // 初始化常数项，或者为0
	int &operator [] (int i) { return a[i]; } // 定义下标访问
	void load(int *from, int n) { // 传入
		len = n;
		memcpy(a, from, sizeof(int)*n);
	}
	void cpyto(int *to, int begin, int len) { // 传出
		memcpy(to, &a[begin], sizeof(int)*len);
	}
	void resize(int n=-1) { // 扩展或收缩长度
		if (n == -1) { while (len > 1 && !a[len-1]) len--; return; } // 不传入参数表明去掉最高位的0的真实长度
		while (len < n) a[len++] = 0; // 保证新项为0
		while (len > n) len--;
	}
	void print() { // 输出
		for (int i = 0; i < len; i++) printf("%d ", a[i]);
	}
} A;

// 多项式求逆。自底向上实现
poly poly_inv(poly A) {
	poly B = poly(qpow(A[0], P-2)); // 边界
	for (int len = 1; len < A.len; len <<= 1) { // 倍增
		static int x[maxn << 2], y[maxn << 2];
		for (int i = 0; i < len << 2; i++) x[i] = y[i] = 0; // 清空数组防止错误
		A.cpyto(x, 0, len << 1); B.cpyto(y, 0, len); // 将信息拷到数组中。注意长度不能太长也不能过短
		ntt(x, len << 2, 1), ntt(y, len << 2, 1);
		for (int i = 0; i < len << 2; i++) x[i] = inc(y[i], inc(y[i], P - 1ll*x[i]*y[i]%P*y[i]%P)); // 求2B'-AB'^2
		ntt(x, len << 2, -1);
		B.load(x, len << 1); // 更新len*2位的值
	}
	B.resize(A.len); // 保证A和B长度相等
	return B;
}

多项式开根

　　给定长度为\(n\)的多项式\(A\)，求项数在\(n\)以内的多项式\(B\)，使得\(B^2\equiv A \pmod{x^n}\)。

　　仍然采用倍增的方法。由于与求逆相似，步骤上的简略参考上文。构造\(B'\)使得\(B'\equiv B \pmod{x^{\lceil \frac{n}{2} \rceil}}\)。然后就有：

\[B-B' \equiv 0 \pmod{x^{\lceil \frac{n}{2} \rceil}}\Rightarrow B^2-2BB'+B'^2 \equiv 0 \pmod{x^n}
\]

　　而\(B^2 \equiv A \pmod{x^n}\)，所以有：

\[A-2BB'+B'^2 \equiv 0 \pmod{x^n} \Rightarrow B = \frac{A+B'^2}{2B'}
\]

　　需要多项式求逆。然后直接套。当\(n=1\)时常数项为模意义下的\(\sqrt{A_0}\)。模板题保证\(A_0=1\)，省去了求解二次剩余的麻烦。复杂度\(\text{O}(n \log n)\)。

// 多项式开根
poly poly_sqrt(poly A) {
	poly B = poly(1); int inv2 = P+1>>1; // 边界和2的逆元
	for (int len = 1; len < A.len; len <<= 1) {
		static int x[maxn << 2], y[maxn << 2], z[maxn << 2];
		for (int i = 0; i < len << 2; i++) x[i] = y[i] = z[i] = 0;
		A.cpyto(x, 0, len << 1), B.cpyto(y, 0, len); // 拷贝信息
		B.resize(len << 1); // 重定B多项式的大小。这里为了使得求解出的逆元长度为2*len
		poly_inv(B).cpyto(z, 0, len << 1); // 拷贝逆的信息
		ntt(x, len << 2, 1), ntt(y, len << 2, 1), ntt(z, len << 2, 1);
		for (int i = 0; i < len << 2; i++) x[i] = 1ll*(x[i]+1ll*y[i]*y[i]%P)*z[i]%P*inv2%P; // 求解(A+B'^2)/(2B')
		ntt(x, len << 2, -1);
		B.load(x, len << 1); // 更新
	}
	B.resize(A.len);
	return B;
}

多项式除法

　　给一个\(n\)次多项式\(F(x)\)和\(m\)次的多项式\(G(x)\)，求\(Q(x)\)和\(R(x)\)，使得满足\(Q(x)\)的次数为\(n-m\)，\(R(x)\)的次数小于\(m\)，且\(F(x)=Q(x)G(x)+R(x)\)。

　　首先定义\(n\)次多项式\(A(x)\)的翻转多项式\(A_{rev}(x)=x^nA(\frac{1}{x})\)，直观上相当于将系数调换。然后我们来转化：

\[F(x)=Q(x)G(x)+R(x) \Rightarrow F(\frac{1}{x})=Q(\frac{1}{x})G(\frac{1}{x})+R(\frac{1}{x}) \Rightarrow x^nF(\frac{1}{x})=x^{n-m}Q(\frac{1}{x})x^mG(\frac{1}{x})+x^{m-1}R(\frac{1}{x})x^{n-m+1}
\]

　　根据定义替换得到上式：

\[F_{rev}(\frac{1}{x})=Q_{rev}(\frac{1}{x})G_{rev}(\frac{1}{x})+x^{n-m+1}R_{rev}(\frac{1}{x})
\]

\[F_{rev}=Q_{rev}G_{rev}+x^{n-m+1}R_{rev}
\]

\[F_{rev} \equiv Q_{rev}G_{rev} \pmod{x^{n-m+1}}
\]

\[\therefore Q_{rev} \equiv \frac{F_{rev}}{G_{rev}} \pmod{x^{n-m+1}}
\]

　　于是\(Q\)通过求逆就能求出来了，然后\(R\)再带回去减一下就出来了。复杂度\(\text{O}(n \log n)\)。

int getsize(int n) { // 获取刚好大于n的2的幂
	int N = 1;
	while (N < n) N <<= 1;
	return N;
}

poly operator - (poly A, poly B) { // 定义减法
	int len = max(A.len, B.len);
	A.resize(len), B.resize(len);
	for (int i = 0; i < len; i++) A[i] = inc(A[i], P-B[i]);
	A.resize(); return A;
}

poly operator * (poly A, poly B) { // 定义乘法
	int len = getsize(A.len + B.len); poly C;
	static int x[maxn << 2], y[maxn << 2];
	for (int i = 0; i < len; i++) x[i] = y[i] = 0;
	A.cpyto(x, 0, A.len), B.cpyto(y, 0, B.len);
	ntt(x, len, 1), ntt(y, len, 1);
	for (int i = 0; i < len; i++) x[i] = 1ll*x[i]*y[i]%P;
	ntt(x, len, -1);
	C.load(x, len), C.resize(); return C;
}

poly operator / (poly A, poly B) { // 定义除法
	A.rev(), B.rev(); // .rev()用来翻转多项式
	int n = A.len - B.len + 1; // 缩短多项式
	A.resize(n), B.resize(n);
	poly C = A * poly_inv(B); C.resize(n); C.rev(); // 求完之后要翻转回来
	return C;
}
...
{
    Q = F / G; // 求Q
    R = F - Q * G; // 求R
}

多项式求ln

　　给一个多项式\(A\)，求\(B\)满足\(B\equiv \ln A \pmod{x^n}\)。

　　前置知识：微积分。

\[B \equiv \ln A \Rightarrow B' \equiv [\ln (A)]' \equiv (\ln A)'A' \equiv \frac{A'}{A} \pmod{x^n}
\]

\[B \equiv \int \frac{A'}{A}\text{d}x+C \pmod{x^n}
\]

　　然后多项式求导中\(C\)一般为\(0\)。复杂度\(\text{O}(n \log n)\)。

poly poly_deri(poly A) { // 多项式求导
	for (int i = 0; i < A.len - 1; i++) A[i] = 1ll*A[i+1]*(i+1)%P;
	A.resize(A.len - 1); return A;
}

poly poly_int(poly A) { // 多项式积分
	for (int i = A.len-1; i; i--) A[i] = 1ll*A[i-1]*inv[i]%P; // 为了减小常数，预处理逆元
	A[0] = 0; return A;
}

poly poly_ln(poly A) { // 多项式求ln
	poly B = poly_inv(A) * poly_deri(A); B.resize(A.len);
	return poly_int(B);
}

多项式求exp

　　给一个多项式\(A\)，求\(B\)满足\(B\equiv e^A \pmod{x^n}\)。

　　这个有点复杂，需要用到泰勒公式和牛顿迭代。泰勒公式前文有讲，牛顿迭代运用到了泰勒展开的东西，这里只提多项式的牛顿迭代。

　　牛顿迭代用来求解满足\(G(F(x)) \equiv 0 \pmod{x^n}\)的多项式\(F(x)\)。怎么迭代？仍然是倍增。

　　当\(n=1\)时，\(G(F(x))\equiv 0\pmod x\)，这个单独解。

　　当\(n>1\)时，假设我们已经求解出\(F_0(x)\)使得\(G(F_0(x)) \equiv 0 \pmod{x^{\lceil \frac{n}{2} \rceil}}\)，根据泰勒展开我们有：

\[G(F(x))\equiv G(F_0(x)) + \frac{G'(F_0(x))}{1!}(F(x)-F_0(x))+\frac{G''(F_0(x))}{2!}(F(x)-F_0(x))^2+\dotsb \pmod{x^n}
\]

　　因为\(F(x) \equiv F_0(x) \pmod{x^{\lceil \frac{n}{2} \rceil}}\)，所以\((F(x)-F_0(x))^2 \equiv 0 \pmod{x^n}\)，从二阶导之后的全部略去，就有了：

\[G(F(x)) \equiv G(F_0(x)) + G'(F_0(x))(F(x)-F_0(x)) \pmod{x^n}
\]

　　又因为\(G(F(x)) \equiv 0 \pmod{x^n}\)，就有了：

\[G(F_0(x))+G'(F_0(x))(F(x)-F_0(x)) \equiv 0 \pmod{x^n}
\]

\[F(x) \equiv F_0(x) - \frac{G(F_0(x))}{G'(F_0(x))} \pmod{x^n}
\]

　　于是我们就可以求解任意多项式函数的零点了。

　　首先变下形：

\[\ln B \equiv A \pmod{x^n}\Rightarrow \ln B-A\equiv 0 \pmod{x^n}
\]

　　令\(G(B(x))=\ln B(x)-A(x)\)，就可以用牛顿迭代求出\(B(x)\)了。中间我们要求\(G'(F_0(x))\)。注意这里自变量是多项式\(F_0(x)\)。

　　所以\(G'(F_0(x)) \equiv \ln F_0(x) - A(x) \equiv \frac{1}{F_0(x)} \pmod{x^n}\)，由于自变量，这里\(A(x)\)求导后为\(0\)。

\[\therefore F(x) \equiv F_0(x) - F_0(x)G(F_0(x)) \equiv F_0(x)(1-\ln F_0(x) + A(x))
\]

　　这样就可以解决了。复杂度\(\text{O}(n \log n)\)。

// 这里保证了A[0]=0，可以得到B[0]=1
poly poly_exp(poly A) {
	poly B = poly(1), C;
	for (int len = 1; len < A.len; len <<= 1) { // 倍增求解
		B.resize(len << 1);
		C = poly(1) - poly_ln(B) + A; C.resize(len << 1); // 分布算防止长度溢出
		B = B * C; B.resize(len << 1);
	}
	B.resize(A.len); return B;
}

　　如果\(A_0 \neq 0\)呢？做不了。

多项式快速幂

　　给一个多项式\(A\)和指数\(k\)，求\(B \equiv A^k \pmod{x^n}\)。

　　直接快速幂？\(\text{O}(n \log n \log k)\)！这个不够优秀，我们有\(\text{O}(n\log n)\)的做法！

　　往下看：

\[\ln(A^k)\equiv \ln B \pmod{x^n} \Rightarrow k\ln A \equiv \ln B \pmod{x^n}\Rightarrow B \equiv e^{k\ln A} \pmod{x^n}
\]

　　这样一来我们只需要：多项式求\(\ln\)，多项式求\(\exp\)即可。

// 没什么东西，就是各种板子来一遍
poly poly_pow(poly A, int k) {
	return poly_exp(k * poly_ln(A));
}

多项式多点求值

　　就是给你一个\(n\)次多项式\(A(x)\)和\(m\)个数，每个数\(x_i\)，求出\(A(x_1)\)、\(A(x_2)\dotsb A(x_m)\)处的取值。

　　直接秦九韶做是\(\text{O}(nm)\)的，不够优秀（但是常数小），我们用构造和分治来解决。

　　构造多项式\(F(x)=\prod_{i=1}^{\lfloor \frac{m}{2} \rfloor} (x-x_i)\)和\(G(x)=\prod_{i=\lfloor \frac{m}{2} + 1\rfloor}^m(x-x_i)\)，这样对于\(\forall i\in [1,\lfloor \frac{m}{2} \rfloor],F(x_i)=0\)、\(\forall i\in [\lfloor \frac{m}{2} \rfloor + 1, m],G(x_i)=0\)，然后求出\(A(x) \bmod F(x)\)的值，也就是多项式除法中剩余的\(R(x)\)。这样有什么用呢？代入我们要求的值，发现\(R(x_i)=A(x_i)\)，因为\(F(x)\)与除法商的乘积为\(0\)。\(A(x)\)是\(n\)次多项式，而\(R(x)\)是次数小于\(\lfloor \frac{m}{2} \rfloor\)多项式，然后将左边一半递归求解，以\(R(x)\)作为新的\(A(x)\)，这样下去多项式次数自然会越来越小。

　　但仍然有一个问题：如何快速求出\(F(x)\)？\(F(x)=F_{left}(x)F_{right}(x)\)。提前分治求解然后存起来即可。注意这里要用\(\text{vector}\)存，否则会爆。

　　时间复杂度：\(\text{O}(n \log^2 n)\)。常数很大？小范围用一用秦九韶有益身心健康。

// 这里poly内用vector代替数组
poly Q[maxn << 4]; // 分治预处理
void divide(int o, int l, int r, int *x) {
	if (l == r) { Q[o].resize(2), Q[o][0] = P-x[l], Q[o][1] = 1; return; } // 边界
	int mid = l+r>>1;
	divide(o<<1, l, mid, x); divide(o<<1|1, mid+1, r, x);
	Q[o] = Q[o<<1] * Q[o<<1|1];
}

void calc(poly A, int o, int l, int r, int *x) {
	if (r-l <= 512) { // 一定范围内用秦九韶展开，我的代码最适宜在512
		for (int i = l; i <= r; i++) {
			int ans = 0; // 运用了循环展开进一步减小常数
			static ull pw[16];
			pw[0] = x[i];
			for (int j = 1; j < 16; j++) pw[j] = 1ll*pw[j-1]*x[i]%P;
			#define I(a,b) A[a]*pw[b]
			for (int j = A.len-1; j >= 16; j -= 16)
				ans = (ans*pw[15]+I(j,14)+I(j-1,13)+I(j-2,12)+I(j-3,11)+I(j-4,10)+I(j-5,9)+I(j-6,8)+I(j-7,7)+I(j-8,6)+I(j-9,5)+I(j-10,4)+I(j-11,3)+I(j-12,2)+I(j-13,1)+I(j-14,0)+A[j-15]) % P;
			#undef I
			for (int j = (A.len-1)&15; ~j; j--) ans = (1ll*ans*x[i]+A[j])%P;
			x[i] = ans;
		}
		return;
	}
	int mid = l+r>>1;
	calc(A % Q[o<<1], o<<1, l, mid, x); calc(A % Q[o<<1|1], o<<1|1, mid+1, r, x); // 否则分治
}

void poly_calc(poly A, int *x, int n) {
	divide(1, 0, n-1, x); calc(A, 1, 0, n-1, x); // 主过程
}

多项式快速插值

　　前文我们讨论过拉格朗日插值。这里的问题变成了求出\(n\)个点插值出来的多项式。

　　看一看拉格朗日插值：

\[f(x)=\sum_{i=1}^n y_i \prod_{j \neq i}\frac{x-x_j}{x_i-x_j}
\]

　　记\(g(x)=\prod_i (x-x_i)\)，那么式子变成：

\[f(x)=\sum_{i=1}^n \frac{y_i}{g(x_i)/(x_i-x_j)} \prod_{j \neq i}(x-x_j)
\]

　　这个\(g(x_i)/(x_i-x_j)\)分母分子都是\(0\)，怎么求呢？

　　引理：洛必达法则。

\[如果\lim_{x\rightarrow a}f(x)=0，\lim_{x\rightarrow a}g(x)=0，则一定有\lim_{x\rightarrow a}\frac{f(x)}{g(x)}=\lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}.
\]

　　证明直接用柯西中值定理。感性理解就是在点无限靠近\(0\)时，\(f(x) \approx f'(x)\)，\(g(x) \approx g'(x)\)，但此时两者都不为\(0\)。

　　于是\(g(x_i)/(x_i-x_j)\)可以直接用\(g'(x_i)/(x_i-x_j)'\)代替，即为\(g'(x_i)\)。

　　式子又变成了：

\[f(x)=\sum_{i=1}^n \frac{y_i}{g'(x_i)} \prod_{j \neq i}(x-x_j)
\]

　　令\(f_{l,r}(x)\)为第\(l\)个点到第\(r\)个点的插值结果（注意这里并不是真正的插值结果），有：

\[\begin{aligned}
f_{l,r}(x)&=\sum_{i=l}^r \frac{y_i}{g'(x_i)} \prod_{j=l, j \neq i}^r(x-x_j) \\
&=\sum_{i=l}^{mid}\frac{y_i}{g'(x_i)}\prod_{j=l, j \neq i}^r(x-x_j)+\sum_{i=mid+1}^{r}\frac{y_i}{g'(x_i)}\prod_{j=l, j \neq i}^r(x-x_j) \\
&=\left(\prod_{i=mid+1}^r (x-x_i)\right) \sum_{i=l}^{mid}\frac{y_i}{g'(x_i)}\prod_{j=l,j \neq i}^{mid} (x-x_j)+\left(\prod_{i=l}^{mid} (x-x_i)\right)\sum_{i=mid+1}^r\frac{y_i}{g'(x_i)}\prod_{j=mid+1,j \neq i}^{r} (x-x_j) \\
&=f_{l,mid}(x)\prod_{i=mid+1}^r(x-x_i)+f_{mid+1,r}(x)\prod_{i=l}^r(x-x_i)
\end{aligned}
\]

　　然后分治求解即可。对于\(\prod\)的求解方法与上一篇相同。复杂度：\(\text{O}(n \log^2 n)\)。

void poly_calc(poly A, int *x, int n) {
	divide(1, 0, n-1, x); calc(A, 1, 0, n-1, x);
}

poly inter(int o, int l, int r, int *x, int *y) {
	if (l == r) return poly(1ll*y[l]*qpow(x[l], P-2)%P);
	int mid = l+r>>1;
	return inter(o<<1, l, mid, x, y)*Q[o<<1|1] + inter(o<<1|1, mid+1, r, x, y)*Q[o<<1]; // 如上
}

poly poly_inter(int *x, int *y, int n) {
	return divide(1, 0, n-1, x), calc(poly_deri(Q[1]), 1, 0, n-1, x), inter(1, 0, n-1, x, y); // 先求出若干连续(x-xi)的乘积，然后根据洛必达法则求值，最后递归算出多项式
} // 传入点，传出插值后的多项式

组合数学

　　主要用来数数求方案数，然后就是一堆球的有(luan)趣(lun)问题。

　　组合：\(n\)个人选出\(m\)个人的方案数，记作\(\begin{aligned}n \choose m\end{aligned}\)。\(\begin{aligned}{n \choose m}=\frac{n!}{m!(n-m)!}\end{aligned}\)。

　　排列：\(n\)个人选出\(m\)个人有顺序排队的不同方案数，记作\(A_n^m\)。显然\(\begin{aligned}A_n^m={n \choose m}m!\end{aligned}\)

　　然后有大名鼎鼎的杨辉三角。

\[\begin{matrix}
&&&&1\\
&&&1& &1\\
&&1&&2&&1\\
&1&&3&&3&&1\\
1&&4&&6&&4&&1
\end{matrix}
\]

　　第\(i\)行第\(j\)个的值：\(\begin{aligned}i-1 \choose j-1\end{aligned}\)。所以我们还有\(\begin{aligned}{n \choose m}={n-1 \choose m-1}+{n-1 \choose m}\end{aligned}\)。组合意义上就是新加入一个人然后看这个人选或不选来分类讨论。

　　然后如果\(\forall x_i:0<x_1<x_2<x_3<\dotsb<x_m\leq n\)，则不等式的整数解个数有\(\begin{aligned}n \choose m\end{aligned}\)种。

　　插板法：将长度为\(n\)的区间划分成\(m\)端，每段不空。问方案数。很显然要在\(n-1\)个端中插入\(m-1\)个板，方案数为\(\begin{aligned}n-1 \choose m-1\end{aligned}\)。如果段的长度可以为\(0\)呢？先往每段塞一个数，就变成上面的问题了，之后取回来即可，方案数为\(\begin{aligned}n+m-1 \choose m-1\end{aligned}\)。

　　有时数学模型是\(\forall x_i:0\leq x_1\leq x_2\leq x_3\leq \dotsb\leq x_m\leq n\)。没关系，把所有的\(x_i\)加上\(i\)就变成了\(0<x_1<x_2<x_3<\dotsb<x_m\leq n+m\)，然后组合数求解即可。

　　组合数性质公式

　　1、\(\begin{aligned}{n \choose m}={n \choose n-m}\end{aligned}\)。很直观看杨辉三角是对称的。也可以从补集上来理解。

　　2、\(\begin{aligned}{n \choose m}={n-1 \choose m-1}+{n-1 \choose m}\end{aligned}\)。

　　3、（二项式定理）\(\begin{aligned}(a+b)^n=\sum_{i=0}^n{n \choose i}a^ib^{n-i}\end{aligned}\)。根据多项式乘多项式，\(a^ib^{n-i}\)的系数可以看成从\(n\)个数中挑出来\(i\)个\(a\)相乘，方案数即为\(\begin{aligned}n \choose i\end{aligned}\)。还有广义二项式定理：\(\begin{aligned}(a+b)^n=\sum_{i=0}^{\infty}{n \choose i}a^ib^{n-i}\end{aligned}\)，其中\(\begin{aligned}{n \choose i}\end{aligned}\)的\(n\)可以为实数，此时\(\begin{aligned}{n \choose m}=\frac{n(n-1)(n-2)\dotsb (n-m+1)}{i!}\end{aligned}\)。

　　4、（顶变底不变）\(\begin{aligned}\sum_{i=0}^m{n+i \choose r}={n+m+1 \choose r+1}\end{aligned}\)。可以用性质\(2\)归纳证明，也可以从组合意义上下手：假设最右边选的人是第\(n+i+1\)位，还剩\(r\)个人没选，就在前面的\(n+i\)个中选。显然最右边位置范围在\(n+1\)到\(n+m+1\)，所以式子显然成立。

　　5、（底变顶不变）\(\begin{aligned}\sum_{i=0}^n{n \choose i}\end{aligned}=2^n\)。用二项式定理看一看\((1+1)^n\)的展开吧。

　　6、\(\begin{aligned}\sum_{i=0}^n(-1)^n{n \choose i}=0\end{aligned}\)。看一看\((1-1)^n\)？

　　7、\(\begin{aligned}\sum_{i=0}^ni\times {n \choose i}=n2^{n-1}\end{aligned}\)。发现是一个组合数构成的三角形，首项\(+\)末项搞一搞就行了。

　　8、（范德蒙恒等式）\(\begin{aligned}\sum_{i=0}^k{n \choose i}{m \choose k-i}={n+m \choose k}\end{aligned}\)。直接从组合意义上看，相当于枚举左边选\(i\)个，右边选\(k-i\)个。最后所有可能加起来等价于\(n+m\)中选\(k\)个。还有推论：\(\begin{aligned}\sum_{i=0}^n{n \choose i}^2={2n \choose n}\end{aligned}\)。用一用性质\(1\)就能发现玄机了。如果想要严谨的证明，通过观察\((1+x)^{m+n}\)的\(x^k\)的系数和\((1+x)^m\)和\((1+x)^n\)乘起来\(x^k\)的系数也能得到。

　　9、\(\begin{aligned}{n \choose m}{m \choose r}={n \choose r}{n-r \choose m-r}\end{aligned}\)。直接从组合意义入手，也就是相当于先划一部分人，再从这部分人中选出来\(r\)个人，反过来考虑如果选中的就是这\(r\)个人，有多少种可能先前划人的可能？实际上就是\(\begin{aligned}{n-r \choose m-r}\end{aligned}\)种。最后选\(r\)个人再乘上方案数\(\begin{aligned}{n \choose r}\end{aligned}\)即可。

Lucas定理

　　定理：当\(p\)是质数时，\(\begin{aligned}{n \choose m} \equiv {\lfloor \dfrac{n}{p} \rfloor \choose \lfloor \dfrac{m}{p} \rfloor}{n \bmod p \choose m \bmod p} \pmod p\end{aligned}\)

　　引理：\((1+x)^p \equiv 1+x^p \pmod p\)

　　\(Proof\)：

\[对左边二项式展开：\sum_{i=0}^p{p \choose i}x^i
\]

\[根据组合数定义，由于当i \neq 0,n时，{p \choose i} \equiv 0，反之\not\equiv 0
\]

\[\therefore 上式=1+x^p
\]

　　下面开始证明。

　　\(Proof\)：

\[令n=pq+r，q=\lfloor \frac{n}{p} \rfloor，则有：(1+x)^n \equiv (1+x)^{pq+r} \equiv ((1+x)^p)^q(1+x)^r\equiv (1+x^p)^q(1+x)^r \pmod p
\]

\[将式子右面展开：\sum_{i=0}^q{q \choose i}x^{ip}\times \sum_{j=0}^r{r \choose j}x^j
\]

\[令m=sp+t，s=\lfloor \frac{m}{p} \rfloor，上面式子中x^m的系数：{q \choose s}{r \choose t}
\]

\[而在(1+x)^n中x^m项的系数为{n \choose m}
\]

\[\therefore {n \choose m}\equiv {q \choose s}{r \choose t} \pmod p
\]

\[命题得证
\]

int fac[maxp], ifac[maxp], inv[maxp]; // 阶乘、阶乘逆元、逆元

void prework(int P) {
	fac[0] = ifac[0] = inv[1] = 1; // 边界
	for (int i = 2; i < P; i++) inv[i] = 1ll*(P-P/i)*inv[P%i]%P; // 求逆元
	for (int i = 1; i < P; i++) fac[i] = 1ll*fac[i-1]*i%P, ifac[i] = 1ll*ifac[i-1]*inv[i]%P; // 求阶乘及其逆元
}

int C(int n, int m, int p) {
	return 1ll*fac[n]*ifac[m]%p*ifac[n-m]%p; // 组合数公式
}

int lucas(int n, int m, int p) {
	return !m ? 1 : 1ll*lucas(n/p, m/p, p)*C(n%p, m%p, p)%p; // lucas定理，注意边界m=0
}

　　复杂度\(\text{O}(p+\log_p n)\)。主要的复杂度在预处理阶乘及其逆元。

　　如果\(p\)不是质数呢？上面的方法变得不太可行了。怎么办呢？

　　发现问题出在求组合数上，逆元不一定存在！原因很简单，因为不互质。

\[\frac{n!}{m!(n-m)!} \bmod p
\]

　　设\(p=p_1^{\alpha_1}p_2^{\alpha_2}\dotsb\)，我们只需求

\[\begin{cases}
\begin{aligned}{n \choose m} \bmod{p_1^{\alpha_1}}\end{aligned} \\
\begin{aligned}{n \choose m} \bmod{p_2^{\alpha_2}}\end{aligned} \\
\dotsb
\end{cases}
\]

　　然后再按照中国剩余定理合并即可。

　　对于单个的情况

\[\frac{n!}{m!(n-m)!} \bmod{p_i^{\alpha_i}}
\]

　　我们把与\(p_i^{\alpha_i}\)互质的因子提出来（即\(p_i\)），得到：

\[\frac{\dfrac{n!}{p_i^x}}{\dfrac{m!}{p_i^y}\dfrac{(n-m)!}{p_i^z}}p_i^{x-y-z} \bmod{p_i^{\alpha_i}}
\]

　　考虑如何求\(\dfrac{n!}{P^x}\bmod P^k\)，接下来的很复杂。

\[\begin{aligned}
n!&=1\times 2\times 3\dotsb \\
&=(P\times 2P \times 3P \dotsb)\left[1 \times 2\dotsb(P-1)\times(P+1)\dotsb\right]\\
&=P^{\lfloor \frac{n}{P} \rfloor}\cdot \lfloor \frac{n}{P} \rfloor ! \cdot \prod_{i=1,P\nmid i}^n i
\end{aligned}
\]

　　发现\(P^{\lfloor \frac{n}{P} \rfloor}\)是其中的因子，\(\lfloor \dfrac{n}{P} \rfloor!\)中可能还含有因子\(P\)，所以我们要递归求解因子个数，这样可以得到\(x,y,z\)。

　　对于剩下部分的值，我们也要求出来。发现\(\begin{aligned}\prod\limits_{i=1,P\nmid i}^n i\end{aligned}\)有循环，可以写成：　　

\[(\prod_{i=1,P\nmid i}^{p^k} i)^{\lfloor \frac{n}{p^k} \rfloor} \prod_{i=1,P\nmid i}^{n \bmod p^k}i
\]

　　之后就可以求出来了。细节看代码。

void prework(int P, int Pk) {
	pdt[0] = 1; // 预处理与Pk互质的数前缀积
	for (int i = 1; i <= Pk; i++)
		pdt[i] = i%P ? 1ll*pdt[i-1]*i%Pk : pdt[i-1];
}

int fac(ll n, int &x, int P, int Pk) {
	return !n ? 1 : (x += n/P, 1ll*fac(n/P, x, P, Pk)*qpow(pdt[Pk], n/Pk, Pk)%Pk*pdt[n%Pk]%Pk); // 处理出n!/P^x，顺道求出来x。公式详细见上文
}

int a[20], b[20];
// p[]是提前筛出来的素数
int exlucas(ll n, ll m, int P) {
	int sz = 0;
	for (int i = 1; P > 1; i++) {
		if (P % p[i]) continue; // p[i]不是P的因子
		b[++sz] = 1;
		int k = 0;
		while (!(P % p[i])) P /= p[i], b[sz] *= p[i]; // 分解因数
		prework(p[i], b[sz]); // 预处理
		int x = 0, y = 0, z = 0;
		a[sz] = 1ll*fac(n, x, p[i], b[sz])*inv(fac(m, y, p[i], b[sz]), b[sz])%b[sz]*inv(fac(n-m, z, p[i], b[sz]), b[sz])%b[sz]*qpow(p[i], x-y-z, b[sz])%b[sz]; // 表达式比较长，但其实就是公式的翻译
	}
	return excrt(a, b, sz); // crt合并出来
}

　　复杂度相差不大，主要在预处理和分解因数上。

　　此被称作扩展\(\bold{Lucas}\)定理。

生成函数

　　(learned from _rqy)

　　生成函数又称母函数，是计数的一大有力工具。生成函数分为普通生成函数（\(\text{OFG}\)）和指数生成函数（\(\text{EFG}\)）。

　　下面先定义下降幂和上升幂。

　　定义下降幂：\(x^{\underline n}=x\times (x-1) \times\dotsb\times (x-n+1)=\prod\limits_{i=0}^{n-1} (x-i)\)

　　定义上升幂：\(x^{\overline n}=x\times (x+1) \times\dotsb\times (x+n-1)=\prod\limits_{i=0}^{n-1} (x+i)\)

　　前置芝士：多项式。

普通生成函数

　　定义普通生成函数

\[F(x)=\sum_{i=0}^{\infty} f_ix^i
\]

　　生成函数看着好像很简单，也不知道有什么威力。先从最简单的看起。

　　数列\(\{1,1,1,1,\dotsb\}\)的生成函数为\(F(x)=\sum\limits_{i=0}^{\infty}x^i\)，我们发现它是个等比数列，即\(F(x)=\dfrac{1}{1-x}\)，这里我们假设\(\mid x \mid<1\)。

　　就像这个生成函数一样，我们可以将一些生成函数化成一个简单的式子，以有限表示无限。有趣吧！再来几个！

　　数列\(\{0,0,1,1,1,\dotsb\}\)的生成函数？相当于最普通的向右平移了\(x^2\)，即\(\dfrac{x^2}{1-x}\)。

　　数列\(\{1,-1,1,-1,\dotsb\}\)？\(\dfrac{1}{1+x}\)。

　　数列\(\{1,c,c^2,c^3,\dotsb\}\)？\(\dfrac{1}{1-cx}\)。

　　数列\(\begin{aligned}\{{n \choose 0},{n \choose 1},{n \choose 2},{n \choose 3},\dotsb\}\end{aligned}\)？\(=(1+x)^n\)。

　　数列\(\{0,1,2,3,\dotsb\}\)？这个有点难，其实是\(\dfrac{1}{(1-x)^2}\)，相当于\(F(x)\)与自身卷一次积得到的结果，也可以从微分的角度理解；如果暂时没看明白，下面会将运算法则。

　　数列\(\{0,1,\dfrac{1}{2},\dfrac{1}{3},\dotsb\}\)？这个更难了，为\(\ln\dfrac{1}{1-x}\)。两边积分即可得到。

　　同理数列\(\{0,1,-\dfrac{1}{2},\dfrac{1}{3},-\dfrac{1}{4},\dotsb\}\)对应的生成函数为\(\ln(1+x)\)，是由\(F(x)=-\dfrac{1}{1+x}\)两边积分得来的。

　　还有很多就不说了，下面谈谈生成函数的运算法则，这样我们可以用来推导更多的生成函数。

\[\alpha F(x)+\beta G(x)=\sum_{i\geq 0}(\alpha f_i+\beta g_i)x^i
\]

\[x^mF(x)=\sum_{i\geq m}f_{i-m}x^i
\]

\[F(cx)=\sum_{i\geq 0}c^if_ix^i
\]

\[F'(x)=\sum_{i\geq 0}(i+1)f_{i+1}x^i
\]

\[\int_0^xF(t)\mathrm dt=\sum_{i>0}\frac{f_{i-1}}{i}x^i
\]

\[F(x)G(x)=\sum_{i\geq 0}\left(\sum_{j+k=i}f_jg_k\right)x^i
\]

　　发现最后一个等式：左边乘积对应右边卷积。

指数生成函数

　　定义指数生成函数

\[F(x)=\sum_{i=0}^{\infty}f_i\frac{x^i}{i!}
\]

　　我们发现\(\begin{aligned}{n \choose m}=\frac{n!}{m!(n-m)!}\end{aligned}\)，如果指数生成函数的第\(m\)项和第\(n-m\)项的值相乘，会得到\(\dfrac{f_mf_{n-m}}{m!(n-m)!}\)，如果再乘上\(n!\)就可以得到\(\begin{aligned}{n \choose m}f_mf_{n-m}\end{aligned}\)。

　　所以可以得到

\[F(x)G(x)=\sum_{i=0}^{\infty}\left( \sum_{j+k=i}{i \choose j}f_jg_k \right)x^i
\]

　　这个适用于排列的计算。

　　同样数列对应指数生成函数。

　　数列\(\{1,1,1,1,\dotsb\}\)对应的生成函数为\(e^x\)。看一看泰勒展开？

　　数列\(\{1,c,c^2,c^3,\dotsb\}\)的生成函数为\(e^{cx}\)。

　　数列\(\{0,1,2,3,\dotsb\}\)的生成函数\(xe^x\)。求个导再平移一下就出来了。

　　指数生成函数的运算法则

\[\alpha F(x)+\beta G(x)=\sum_{i\geq 0}(\alpha f_i+\beta g_i)\frac{x^i}{i!}
\]

\[x^mF(x)=\sum_{i\geq m}n^{\underline m}f_{i-m}\frac{x^i}{i!}
\]

\[F(cx)=\sum_{i\geq 0}c^if_i\frac{x^i}{i!}
\]

\[F'(x)=\sum_{i\geq 0}f_{i+1}\frac{x^i}{i!}
\]

\[\int_0^xF(t)\mathrm dt=\sum_{i>0}f_{i-1}\frac{x^i}{i!}
\]

　　求导积分注意有的因数被约掉了。再加上上面的乘法，基本上构成了指数生成函数的运算法则，这些不难推导。

生成函数的运用

求通项公式

　　利用递归式的特性，构造生成函数，然后通过解方程的形式得到式子后再展开得到信息。

Fibonacci数列

　　数列\(\{0,1,1,2,3,5,8,\dotsb\}\)被称为\(\text{Fibonacci}\)数列，它有以下递推式

\[f_n=
\begin{cases}
0&n=0\\
1&n=1\\
f_{n-1}+f_{n-2}&n\geq 2 \\
\end{cases}
\]

　　定义\(\text{Fibonacci}\)生成函数为\(\sum\limits_{i\geq 0}f_ix^i\)，则根据递推式，我们有：

\[\begin{aligned}
F(x)&=\sum_{i\geq 0}f_ix^i\\
&=\sum_{i\geq 0}(f_{i-2}+f_{i-1}+[i==1])x^i\\
&=\sum_{i\geq 0}f_ix^{i+2}+\sum_{i\geq 0}f_ix^{i-1}+x\\
&=x^2\sum_{i\geq 0}f_ix^i+x\sum_{i\geq 0}f_ix^i+x\\
&=x^2F(x)+xF(x)+x
\end{aligned}
\]

　　加上一个单位函数是为了保证边界\(i=1\)时为\(1\)。这样我们可以解出来\(F(x)=\dfrac{x}{1-x-x^2}\)，进一步展开得到：

\[F(x)=\frac{x}{1-x-x^2}=\dfrac{1}{\sqrt 5}\left(\frac{1}{1-\phi x}-\frac{1}{1-\hat\phi x}\right)
\]

　　其中\(\phi=\dfrac{1+\sqrt 5}{2}\)，\(\hat \phi=\dfrac{1-\sqrt 5}{2}\)。

　　然后因为\(\dfrac{1}{1-cx}=1+cx+c^2x^2+\dotsb\)，得到

\[F(x)=\sum_{i\geq 0} \frac{\phi^i-\hat\phi^i}{\sqrt 5}x^i
\]

　　得知第\(n\)项的系数为\(\dfrac{\phi^i-\hat\phi^i}{\sqrt 5}\)，即为\(\text{Fibonacci}\)的第\(n\)项的值。

Catalan数

　　\(\text{Catalan}\)数的递推式：

\[\begin{cases}
1&n=0\\
\sum\limits_{i<n} f_if_{n-i-1}&n>1
\end{cases}
\]

　　定义卡特兰数的生成函数：\(F(x)=\sum\limits_{i \geq 0}f_ix^i\)，由递推式得到：

\[\begin{aligned}
F(x)&=\sum_{i\geq 0}f_ix^i\\
&=\sum_{i\geq 0}\left([x==0]+\sum_{x<i}f_xf_{i-x-1}\right)x^i\\
&=1+\sum_{i\geq 0}x^i\sum_{x<i}f_xf_{i-x-1} \\
&=1+x\sum_{i\geq 0}\left(\sum_{x<i}f_xf_{i-1-x}\right)x^{i-1} \\
&=1+xF^2(x)
\end{aligned}
\]

　　解得\(F(x)=\dfrac{1\pm \sqrt{1-4x}}{2x}\)，有一个\(\pm\)怎么办？

　　（坑坑坑）先看用母函数推卡特兰数通项公式 知乎吧（博主疯了）

斯特林数

　　组合数学中有两类斯特林数：第一类斯特林数、第二类斯特林数。

第一类斯特林数

　　第一类斯特林数表示将\(n\)个不同元素构成\(m\)个圆排列的数目，记作\(s(n,m)\)。能推出递推式

\[s(n,m)=s(n-1,m-1)+(n-1)\times s(n-1,m)
\]

　　特别的，\(s(0,0)=1\)，\(s(n,0)=0\)，\(s(n,n)=1\)。

　　斯特林数一般求一行或一列。

求一行

　　有一个式子：

\[\sum_{k=0}^ns(n,k)x^k=\prod_{i=0}^{n-1}(x+i)=x^{\overline n}
\]

　　\(Proof\)：

\[我们用归纳法：当n=0时，显然成立
\]

\[当n>0时，有：
\]

\[\begin{aligned}
x^{\overline{n+1}}&=(x+n)\times x^{\overline n}=(x+n)\sum_{k=0}^ns(n,k)x^k \\
&=\sum_{k=1}^{n+1}s(n,k-1)x^k+\sum_{k=0}^nns(n,k)x^k \\
&=\sum_{k=1}^{n}[s(n,k-1)x^k+ns(n,k)x^k]+s(n,n)x^{n+1}+ns(n,0) \\
&=\sum_{k=0}^ns(n+1,k)x^k+s(n+1,n+1)x^{n+1} \\
&=\sum_{k=0}^{n+1}s(n+1,k)x^k
\end{aligned}
\]

　　如何求解呢？可以用分治\(\text{FFT}\)，\(\text{O}(n\log^2 n)\)。但不够优秀，我们还有\(\text{O}(n\log n)\)的方法。

　　考虑倍增。假设我们求出了\(x^{\overline n}\)对应的多项式\(\sum\limits_{i=0}^n a_ix^i\)，我们来求一下\((x+n)^{\overline n}\)。

\[\begin{aligned}
(x+n)^{\overline n}&=\sum_{i=0}^na_i(x+n)^i \\
&=\sum_{i=0}^na_i\sum_{j=0}^i{i \choose j}x^jn^{i-j} \\
&=\sum_{j=0}^nx^j\sum_{i=j}^na_i{i \choose j}n^{i-j} \\
&=\sum_{j=0}^nx^j\sum_{i=j}^n\frac{a_ii!}{j!(i-j)!}n^{i-j} \\
&=\sum_{j=0}^nx^j\left(\frac{1}{j!}\sum_{i=j}^na_ii!\frac{n^{i-j}}{(i-j)!}\right)
\end{aligned}
\]

　　后面式子翻转一下卷积即可求出。复杂度为\(\text{T}(n)=\text{T}(n/2)+\text{O}(n\log n)=\text{O}(n\log n)\)。

　　递归求解。对于余项直接乘。

(咕咕咕)

求一列

　　定义环排列指数生成函数

\[f(x)=\sum_{i>0}(i-1)!\frac{x^i}{i!}
\]

　　因为\(n\)个数的环排列有\((n-1)!\)种。用指数生成函数满足划分环大小时，在同一个环内的方案不被重复计算。

　　所以有：

\[s(i,m)=[x^i]\frac{1}{m!}f(x)^m
\]

　　最后是由于划分\(m\)个环大小的过程中有\(m!\)种相同的情况，所以要除去。

　　多项式快速幂即可。注意要偏移下标，因为常数项为\(0\)。

(咕咕咕)

第二类斯特林数

　　第二类斯特林数表示将\(n\)个不同的元素放到\(m\)个相同集合里的方案数，记作\(S(n,m)\)。也有递推式

\[S(n,m)=S(n-1,m-1)+m\times S(n-1,m)
\]

二项式反演

　　如果：

\[F(n)=\sum_{i=0}^n(-1)^i{n \choose i}f(i)
\]

　　那么有：

\[f(n)=\sum_{i=0}^n(-1)^i{n \choose i}F(i)
\]

　　此被称作二项式反演。

　　\(Proof\)：

\[\begin{aligned}
&\sum_{i=0}^n(-1)^i{n \choose i}F(i)\\
=&\sum_{i=0}^n(-1)^i{n \choose i}\sum_{j=0}^{i}(-1)^j{i \choose j}f(j)\\
=&\sum_{i=0}^n\sum_{j=0}^i(-1)^{i-j}{n \choose i}{i \choose j}f(j)\\
=&\sum_{j=0}^n\sum_{i=j}^n(-1)^{i-j}{n \choose i}{i \choose j}f(j)\\
=&\sum_{j=0}^n\sum_{i=j}^n(-1)^{i-j}{n \choose j}{n-j \choose i-j}f(j)\\
=&\sum_{j=0}^n{n \choose j}f(j)\sum_{i=j}^n(-1)^{i-j}{n-j \choose i-j}\\
=&\sum_{j=0}^n{n \choose j}f(j)\sum_{i=0}^{n-j}(-1)^{i}{n-j \choose i}\\
=&f(n)
\end{aligned}
\]

　　最后一步是根据\(\begin{aligned}\sum\limits_{i=0}^n(-1)^i{n \choose i}=\begin{cases}0&(n>0)\\1&(n=0)\end{cases}\end{aligned}\)得来的。

　　还有一个比较常用的式子：

　　由：

\[F(n)=\sum_{i=0}^n{n \choose i}f(i)
\]

　　得到：

\[f(n)=\sum_{i=0}^n(-1)^{n-i}{n \choose i}F(i)
\]

　　证明类似。

拉格朗日反演

　　定义两个多项式\(f(x)\)和\(g(x)\)，如果\(f(g(x))=x\)成立，此时显然\(f(g(x))=g(f(x))\)，且\([x^0]f(x)=0\)，\([x^1]f(x)\times [x^1]g(x)=1\)，那么有

　　定理\(1\)：

\[[x^n]f(x)=\frac{1}{n}[x^{n-1}](\frac{x}{g(x)})^n
\]

　　\(Proof\)

\[根据f(g(x))=x得到:\sum_{i=1}^{\infty}f_ig^i(x)=x
\]

\[两边求导:\sum_{i=0}^{\infty}if_ig^{i-1}(x)g’(x)=1
\]

\[两边同时除去g^n(x):\sum_{i=0}^{\infty}if_ig^{i-n-1}(x)g’(x)=\frac{1}{g^n(x)}
\]

\[\therefore [x^{-1}]\sum_{i=0}^{\infty}if_ig^{i-n-1}(x)g’(x)=[x^{-1}]\frac{1}{g^n(x)}
\]

\[此时要分类讨论
\]

\[当i\neq n时，g^{n-i-1}(x)g’(x)=\frac{1}{n-i}g^{n-i}，这个可以从右往左直接链式法则得到
\]

\[多项式的任意阶导，其x^{-1}项系数一定为0
\]

\[\therefore 上式=0
\]

\[当i=n时，我们要求g^{-1}(x)g’(x)，直接展开得
\]

\[\begin{aligned}
&\frac{g_1+2g_2x+3g_3x^2+\dotsb}{g_1x+g_2x^2+g_3x^3+\dotsb}\\
=& \frac{g_1+2g_2x+3g_3x^2+\dotsb}{g_1x}\cdot\frac{1}{1+\frac{g_2}{g_1}x+\frac{g_3}{g_1}x^2+\dotsb}
\end{aligned}
\]

\[由于g_1\neq 0得到这一步
\]

\[后面式子常数项不为0所以一定可逆
\]

\[根据展开x的负指数幂的系数一定为0，且求逆后的常数项一定为1
\]

\[前面的式子显然得到[x^{-1}]=1
\]

\[综上，[x^{-1}]\sum_{i=0}^{\infty}if_ig^{i-n-1}(x)g’(x)=nf_n=[x^{-1}]\frac{1}{g^n(x)}
\]

\[f_n=[x^{-1}]\frac{1}{n}\frac{1}{g^n(x)}
\]

\[为了方便求解系数，右边通过乘x^n来平移系数
\]

\[\therefore [x^n]f(x)=[x^{n-1}]\frac{1}{n}(\frac{x}{g(x)})^n
\]

单位根反演

　　定理：\(\dfrac{\sum\limits_{k=1}^n \omega_n^{dk}}{n}=[n\mid d]\)。\([state]\)是单位函数。

　　不证，在\(\text{FFT}\)的求和引理中有。