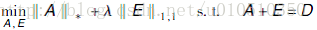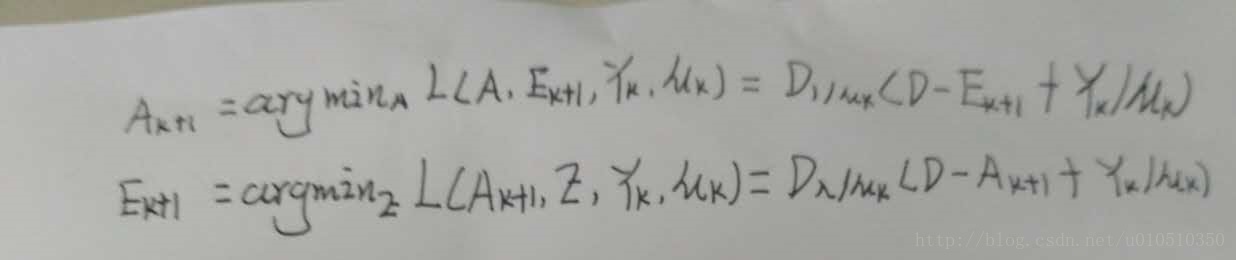Rubost PCA 优化
Rubost PCA 优化
最近一直在看Robust PCA做背景建模的paper, 顺便总结了一下了Robust PCA.前面一篇博客介绍了PCA与Robust PCA区别,本篇博客总结Robust PCA 常见的优化方法,欢迎交流学习。在这里强烈推荐一篇博客Rachel Zhang的Robust PCA 学习笔记。
1.预备知识
2.问题描述
许多实际应用中已知的数据矩阵D往往是低秩或近似低秩的,但存在随机幅值任意大且分布稀疏的误差破坏了原有数据的低秩性,为了恢复矩阵D的低秩结构,可将矩阵D分解为两个矩阵之和,即D=A+E,其中矩阵A和E未知,但A是低秩的,E是稀疏的。 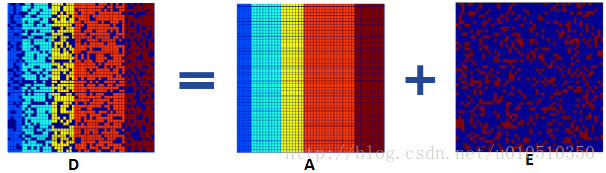
当矩阵E的元素服从独立同分布的高斯分布时,可用经典的PCA来获得最优的矩阵A,即转换为如下最优化问题: 
当E为稀疏的大噪声矩阵时,同时引入折中因此,此问题可转化为如下优化问题: 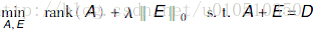
上式中秩函数、0范数均非凸,变成了NP-hard问题,需要对其松弛,方可进行优化。由范数知识可知,核范数是秩函数的凸包,1范数是0范数的凸包,所以上述NP-hard问题松弛后可转化凸优化问题:
3.Rubost PCA优化
增广拉格郎日乘子法(Augmented Lagrang Multipliers)
交替方向法(Alternating Direction Methods)
ADM 是对ALM的改善,加快了收敛速度,又称为不精确拉格朗日乘子法。
迭代阈值法(Iterative Thresholding)
**加速近端梯度(Accelerated Proximal Gradient)
**
将优化问题式的等式约束松弛到目标函数中,得到如下的拉格朗日函数:
f(A,E)的Frechet梯度Lipschitz连续性推导 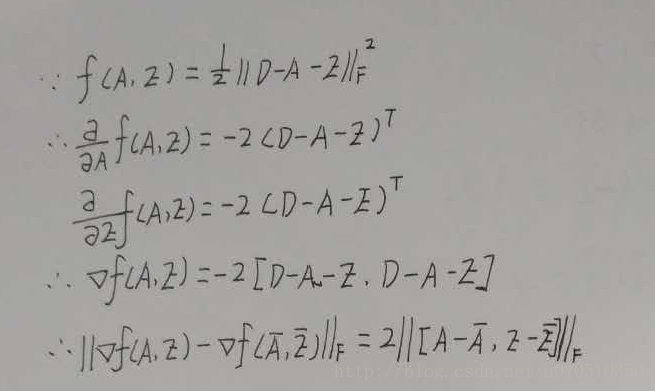
f(x)二次逼近推导
4.Rubost PCA优化总结
IT算法的迭代形式简单且收敛,但收敛速度比较慢,且很难选取合适的步长;APG与IT算法类似,但它却大大降低了迭代次数;ALM比APG快很多,而且ALM可以达到较高的精度,需要较低的存储空间。不精确拉格朗日乘子法(IALM)改善了EALM,不需要求解精确解,速度较快。
参考
1. The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices
2. Fast Convex Optimization Algorithms for Exact Recovery of a Corrupted Low-Rank Matrix
3. A Singular Value Thresholding Algorithm for Matrix Completion
4. Sparse and Low-Rank Matrix Decomposition via Alternating Direction Methods
5. Robust Principal Component Analysis
6. http://blog.csdn.net/tiandijun/article/details/44917237
Rubost PCA 优化的更多相关文章
- 机器学习公开课笔记(8):k-means聚类和PCA降维
K-Means算法 非监督式学习对一组无标签的数据试图发现其内在的结构,主要用途包括: 市场划分(Market Segmentation) 社交网络分析(Social Network Analysis ...
- Andrew Ng机器学习课程笔记--week8(K-means&PCA)
Unsupervised Learning 本周我们讲学习非监督学习算法,会学习到如下概念 聚类(clustering) PCA(Principal Componets Analysis主成分分析), ...
- 主成分分析(PCA)原理总结
主成分分析(Principal components analysis,以下简称PCA)是最重要的降维方法之一.在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用.一般我们提到降维最容易想到的算法就 ...
- 数据降维技术(1)—PCA的数据原理
PCA(Principal Component Analysis)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降 ...
- 主成分分析 (PCA) 与其高维度下python实现(简单人脸识别)
Introduction 主成分分析(Principal Components Analysis)是一种对特征进行降维的方法.由于观测指标间存在相关性,将导致信息的重叠与低效,我们倾向于用少量的.尽可 ...
- 机器学习笔记----四大降维方法之PCA(内带python及matlab实现)
大家看了之后,可以点一波关注或者推荐一下,以后我也会尽心尽力地写出好的文章和大家分享. 本文先导:在我们平时看NBA的时候,可能我们只关心球员是否能把球打进,而不太关心这个球的颜色,品牌,只要有3D效 ...
- PCA原理与实践
在对数据进行预处理时,我们经常会遇到数据的维数非常之大,如果不进行相应的特征处理,那么算法的资源开销会很大,这在很多场景下是我们不能接受的.而对于数据的若干维度之间往往会存在较大的相关性,如果能将数据 ...
- PRML读书会第十二章 Continuous Latent Variables(PCA,Principal Component Analysis,PPCA,核PCA,Autoencoder,非线性流形)
主讲人 戴玮 (新浪微博: @戴玮_CASIA) Wilbur_中博(1954123) 20:00:49 我今天讲PRML的第十二章,连续隐变量.既然有连续隐变量,一定也有离散隐变量,那么离散隐变量是 ...
- PCA算法是怎么跟协方差矩阵/特征值/特征向量勾搭起来的?
PCA, Principle Component Analysis, 主成份分析, 是使用最广泛的降维算法. ...... (关于PCA的算法步骤和应用场景随便一搜就能找到了, 所以这里就不说了. ) ...
随机推荐
- 动物细胞结构模型 | animal cell structure
现在大家已经对细胞结构单位习以为常,但在细胞发现之前,这是不可思议的,千奇百怪的生命世界居然有一个统一的基本单位. 这里简单回忆一下经典的细胞结构: 参考YouTube视频: Biology: Cel ...
- PHP课程环境安装总结文档
phpStudy的安装 1.找一个硬盘根目录,比如这里我使用E盘,在E盘根目录创建一个php的文件夹,进入php文件夹,如下图所示 2.在步骤1的php文件夹下再建立一个文件夹php_dev,如下图所 ...
- vue-router 利用url传递参数
vue-router 利用url传递参数 :冒号的形式传递参数 在路由配置文件里以:冒号的形式传递参数,这就是对参数的绑定. 1. 在配置文件里以冒号的形式设置参数.我们在/src/router/i ...
- python3 selenium模块Chrome设置代理ip的实现
python3 selenium模块Chrome设置代理ip的实现 selenium模块Chrome设置代理ip的实现代码: from selenium import webdriver chrome ...
- sublime 删除重复行
sublime 删除重复行 - 国内版 Binghttps://cn.bing.com/search?q=sublime+%E5%88%A0%E9%99%A4%E9%87%8D%E5%A4%8D%E8 ...
- netty5拆包问题解决实例
基于之前的例子(参见netty5自定义私有协议实例),我们修改下客户端handler,让发送的数据超过1024字节: NettyClientHandler: /** * 构造PCM请求消息体 * * ...
- Spring cloud微服务安全实战-6-4权限控制改造
授权,权限的控制 令牌里的scope包含fly就有权限访问.根据Oauth的scope来做权限控制, 要让@PreAuthorize生效,就要在启动类里面写一个注解. 里面有一个属性叫做,就是在方法的 ...
- windows10 环境下的RabbitMQ安装步骤(图文)
第一步:下载并安装erlang 原因:RabbitMQ服务端代码是使用并发式语言Erlang编写的,安装Rabbit MQ的前提是安装Erlang. 下载地址:http://www.erlang.or ...
- SpringCloud学习成长之十四 服务注册(consul)
这篇文章主要介绍 spring cloud consul 组件,它是一个提供服务发现和配置的工具.consul具有分布式.高可用.高扩展性. 一.consul 简介 consul 具有以下性质: 服务 ...
- intellij 插件的使用
目录 intellij 插件的使用 插件的设置 插件推荐 @(目录) intellij 插件的使用 插件的设置 在 IntelliJ IDEA 的安装讲解中我们其实已经知道,IntelliJ IDEA ...