LR 算法总结--斯坦福大学机器学习公开课学习笔记

在有监督学习里面有几个逻辑上的重要组成部件[3]，初略地分可以分为：模型，参数 和 目标函数。（此部分转自 XGBoost 与 Boosted Tree）

一、模型和参数 
  模型指给定输入xi如何去预测 输出 yi。我们比较常见的模型如线性模型（包括线性回归和logistic regression）采用

二、目标函数：损失 + 正则

模型和参数本身指定了给定输入我们如何做预测，但是没有告诉我们如何去寻找一个比较好的参数，这个时候就需要目标函数登场了。一般的目标函数包含下面两项

常见的误差函数有平方误差、交叉熵等，而对于线性模型常见的正则化项有L2正则和L1正则。

三、优化算法

讲了这么多有监督学习的基本概念，为什么要讲这些呢？ 是因为这几部分包含了机器学习的主要成分，也是机器学习工具设计中划分模块比较有效的办法。其实这几部分之外，还有一个优化算法，就是给定目标函数之后怎么学的问题。之所以我没有讲优化算法，是因为这是大家往往比较熟悉的“机器学习的部分”。而有时候我们往往只知道“优化算法”，而没有仔细考虑目标函数的设计的问题，比较常见的例子如决策树的学习，大家知道的算法是每一步去优化gini entropy，然后剪枝，但是没有考虑到后面的目标是什么。

然后看逻辑回归（LR）算法，主要参考斯坦福大学机器学习公开课，http://www.iqiyi.com/playlist399002502.html

逻辑回归是一种分类算法，而不是一种回归。逻辑回归采用sigmod函数，这是一个自变量取值在整个实数空间，因变量取值在0-1之间的函数，可以将变量的变化映射到0-1之间，从而获得概率值。

sigmod函数形式如下

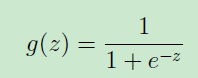
通过将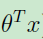代入sigmod函数，可以得到如下形式：

这样我们得到了模型和参数，下一步我们确定目标函数，逻辑回归的损失函数是交叉熵函数，求得参数采用的优化算法是最大似然。

假设

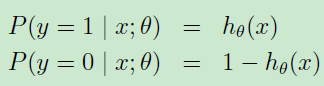
可以更加简洁的写作

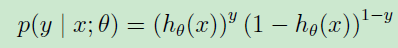
根据最大似然算法，所求的模型应该使得取得样本的情况的概率越大越好，假设样本相互之间都是独立的，则可以如下表示用模型取得样本情况的概率

也就是独立事件同时发生的概率。为了方便处理，取log则

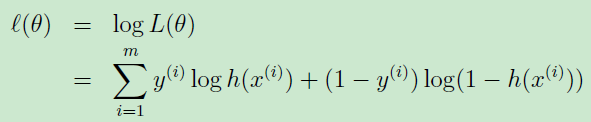
这也就是逻辑回归的损失函数。

求解这个目标函数采用随机梯度下降的方法即可，

由于sigmod函数的如下特性

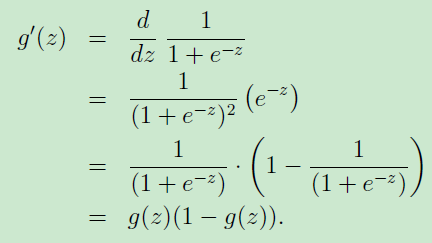
可以简单的将求梯度的式子简化如下

这样就可以通过样本不停的更新，直至找到满足要求的参数。

3: Principles of Data Mining, David Hand et al,2001. Chapter 1.5 Components of Data Mining Algorithms, 将数据挖掘算法解构为四个组件：1）模型结构（函数形式，如线性模型），2）评分函数（评估模型拟合数据的质量，如似然函数，误差平方和，误分类率），3）优化和搜索方法（评分函数的优化和模型参数的求解），4）数据管理策略（优化和搜索时对数据的高效访问）。