数据挖掘系列（4）使用weka做关联规则挖掘

　　前面几篇介绍了关联规则的一些基本概念和两个基本算法，但实际在商业应用中，写算法反而比较少，理解数据，把握数据，利用工具才是重要的，前面的基础篇是对算法的理解，这篇将介绍开源利用数据挖掘工具weka进行管理规则挖掘。

weka数据集格式arff

　　arff标准数据集简介

　　weka的数据文件后缀为arff（Attribute-Relation File Format，即属性关系文件格式），arff文件分为注释、关系名、属性名、数据域几大部分，注释用百分号开头%，关系名用@relation申明，属性用@attribute什么，数据域用@data开头，看这个示例数据集（安装weka后，可在weka的安装目录/data下找到weather.numeric.arff）：　　

%weather dataset
@relation weather
 
@attribute outlook {sunny, overcast, rainy}
@attribute temperature numeric
@attribute humidity numeric
@attribute windy {TRUE, FALSE}
@attribute play {yes, no}
 
@data
sunny,85,85,FALSE,no
sunny,80,90,TRUE,no
overcast,83,86,FALSE,yes
rainy,70,96,FALSE,yes
rainy,68,80,FALSE,yes
rainy,65,70,TRUE,no
overcast,64,65,TRUE,yes
sunny,72,95,FALSE,no
sunny,69,70,FALSE,yes
rainy,75,80,FALSE,yes
sunny,75,70,TRUE,yes
overcast,72,90,TRUE,yes
overcast,81,75,FALSE,yes
rainy,71,91,TRUE,no

　　当数据是数值型，在属性名的后面加numeric，如果是离散值（枚举值），就用一个大括号将值域列出来。@data下一行后为数据记录，数据为矩阵形式，即每一个的数据元素个数相等，若有缺失值，就用问号?表示。

　　arff稀疏数据集　　　

　　我们做关联规则挖掘，比如购物篮分析，我们的购物清单数据肯定是相当稀疏的，超市的商品种类有上10000种，而每个人买东西只会买几种商品，这样如果用矩阵形式表示数据显然浪费了很多的存储空间，我们需要用稀疏数据表示，看我们的购物清单示例（basket.txt)：　　

freshmeat dairy confectionery
freshmeat    confectionery
cannedveg    frozenmeal    beer    fish
dairy    wine
freshmeat    wine    fish
fruitveg    softdrink
beer
fruitveg    frozenmeal
fruitveg    fish
fruitveg    freshmeat    dairy    cannedveg    wine    fish
fruitveg    fish
dairy    cannedmeat    frozenmeal    fish

　　数据集的每一行表示一个去重后的购物清单，进行关联规则挖掘时，我们可以先把商品名字映射为id号，挖掘的过程只有id号就是了，到规则挖掘出来之后再转回商品名就是了，retail.txt是一个转化为id号的零售数据集，数据集的前面几行如下：　　

0    1    2    3    4    5    6    7    8    9    10    11    12    13    14    15    16    17    18    19    20    21    22    23    24    25    26    27    28
30    31    32
33    34    35
36    37    38    39    40    41    42    43    44    45    46
38    39    47    48
38    39    48    49    50    51    52    53    54    55    56    57    58
32    41    59    60    61    62
3    39    48
63    64    65    66    67    68
32    69

　　这个数据集的商品有16469个，一个购物的商品数目远少于商品中数目，因此要用稀疏数据表，weka支持稀疏数据表示，但我在运用apriori算法时有问题，先看一下weka的稀疏数据要求：稀疏数据和标准数据的其他部分都一样，唯一不同就是@data后的数据记录，示例如下(basket.arff)：

@relation 'basket'
@attribute fruitveg {F, T}
@attribute freshmeat {F, T}
@attribute dairy {F, T}
@attribute cannedveg {F, T}
@attribute cannedmeat {F, T}
@attribute frozenmeal {F, T}
@attribute beer {F, T}
@attribute wine {F, T}
@attribute softdrink {F, T}
@attribute fish {F, T}
@attribute confectionery {F, T}
@data
{1 T, 2 T, 10 T}
{1 T, 10 T}
{3 T, 5 T, 6 T, 9 T}
{2 T, 7 T}
{1 T, 7 T, 9 T}
{0 T, 8 T}
{6 T}
{0 T, 5 T}
{0 T, 9 T}
{0 T, 1 T, 2 T, 3 T, 7 T, 9 T}
{0 T, 9 T}
{2 T, 4 T, 5 T, 9 T}

　　可以看到

freshmeat dairy confectionery
freshmeat    confectionery

　　表示为了：

{1 T, 2 T, 10 T}
{1 T, 10 T

　　稀疏数据的表示格式为：{<属性列号><空格><值>,...,<属性列号><空格><值>}，注意每条记录要用大括号，属性列号不是id号，属性列号是从0开始的，即第一个@attribute 后面的属性是第0个属性，T表示数据存在。

规则挖取

　　我们先用标准数据集normalBasket.arff[1]试一下，weka的apriori算法和FPGrowth算法。

　　1、安装好weka后，打开选择Explorer

　　2、打开文件

　　

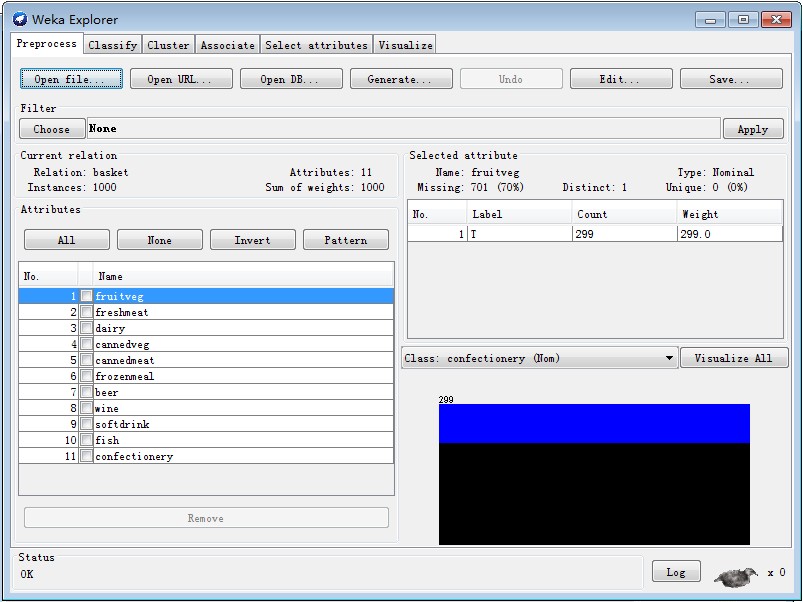
　　3、选择关联规则挖掘，选择算法

　　

　　4、设置参数

　

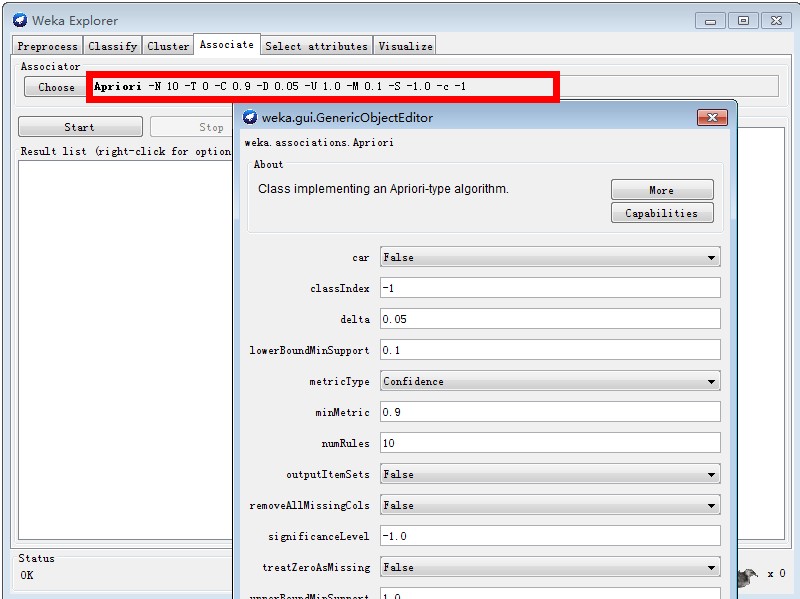
　　参数主要是选择支持度(lowerBoundMinSupport)，规则评价机制metriType（见上一篇）及对应的最小值，参数设置说明如下[2]：

.        car 如果设为真，则会挖掘类关联规则而不是全局关联规则。
.        classindex 类属性索引。如果设置为-，最后的属性被当做类属性。
.        delta 以此数值为迭代递减单位。不断减小支持度直至达到最小支持度或产生了满足数量要求的规则。
.        lowerBoundMinSupport 最小支持度下界。
.        metricType 度量类型。设置对规则进行排序的度量依据。可以是：置信度（类关联规则只能用置信度挖掘），提升度(lift)，杠杆率(leverage)，确信度(conviction)。
在 Weka中设置了几个类似置信度(confidence)的度量来衡量规则的关联程度，它们分别是：
a)        Lift ： P(A,B)/(P(A)P(B)) Lift=1时表示A和B独立。这个数越大(>)，越表明A和B存在于一个购物篮中不是偶然现象,有较强的关联度.
b)        Leverage :P(A,B)-P(A)P(B)Leverage=0时A和B独立，Leverage越大A和B的关系越密切
c)        Conviction:P(A)P(!B)/P(A,!B) （!B表示B没有发生） Conviction也是用来衡量A和B的独立性。从它和lift的关系（对B取反，代入Lift公式后求倒数）可以看出，这个值越大, A、B越关联。
.        minMtric 度量的最小值。
.        numRules 要发现的规则数。
.        outputItemSets 如果设置为真，会在结果中输出项集。
.        removeAllMissingCols 移除全部为缺省值的列。
 
.    significanceLevel 重要程度。重要性测试（仅用于置信度）。
 
.    upperBoundMinSupport 最小支持度上界。 从这个值开始迭代减小最小支持度。
 
.    verbose 如果设置为真，则算法会以冗余模式运行。

设置好参数后点击start运行可以看到Apriori的运行结果：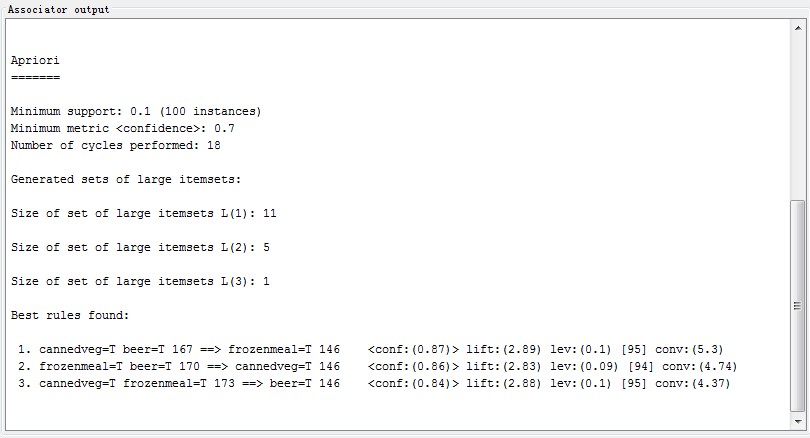

　　FPGrowth运行的结果是一样的：

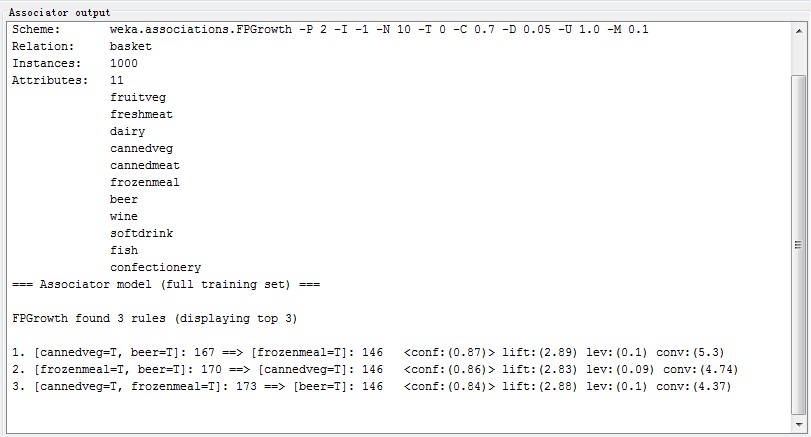
　　每条规则都带有出现次数、自信度、相关度等数值。

　　下面测一个大一点的数据集retail.arff[1]（retail.arff是由retail.txt转化而来，为了不造成误解，我在id好前加了一个"I"，比如2变为I2），这个数据用的稀疏数据表示方法，数据记录有88162条，用Apriori算法在我的2G电脑上跑不出来，直接内存100%，用FPGrowth可以轻松求出，看一下运行结果：　　

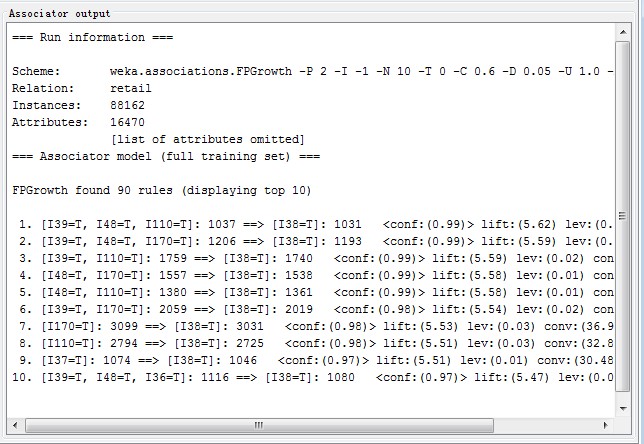
　　其他参数可以自己调整比较。

参考文献：

　　[1].本文用的所有数据集basket.txt,basket.arff,normalBasket.arff,retail.txt,retail.arff都在这里可下载.

　　[2].weka Apriori算法实例操作详解:http://blog.csdn.net/haosijia929/article/details/5596939

感谢阅读，欢迎回帖交流

转置请注明出处：www.cnblogs.com/fengfenggirl