Determining if a point lies on the interior of a polygon

Determining if a point lies on the interior of a polygon

Written by Paul Bourke  November 1987

Solution 1 (2D)

The following is a simple solution to the problem often encountered in computer graphics, determining whether or not a point (x,y) lies inside or outside a 2D polygonally bounded plane. This is necessary for example in applications such as polygon filling on raster devices, hatching in drafting software, and determining the intersection of multiple polygons.

Consider a polygon made up of N vertices (x_i,y_i) where i ranges from 0 to N-1. The last vertex (x_N,y_N) is assumed to be the same as the first vertex (x₀,y₀), that is, the polygon is closed. To determine the status of a point (x_p,y_p) consider a horizontal ray emanating from (x_p,y_p) and to the right. If the number of times this ray intersects the line segments making up the polygon is even then the point is outside the polygon. Whereas if the number of intersections is odd then the point (x_p,y_p) lies inside the polygon. The following shows the ray for some sample points and should make the technique clear.

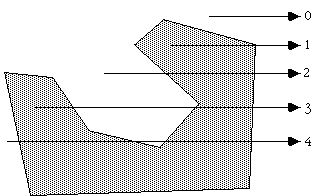
Note: for the purposes of this discussion 0 will be considered even, the test for even or odd will be based on modulus 2, that is, if the number of intersections modulus 2 is 0 then the number is even, if it is 1 then it is odd.

The only trick is what happens in the special cases when an edge or vertex of the polygon lies on the ray from (x_p,y_p). The possible situations are illustrated below.

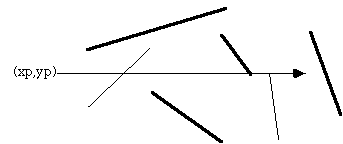
The thick lines above are not considered as valid intersections, the thin lines do count as intersections. Ignoring the case of an edge lying along the ray or an edge ending on the ray ensures that the endpoints are only counted once.

Note that this algorithm also works for polygons with holes as illustrated below

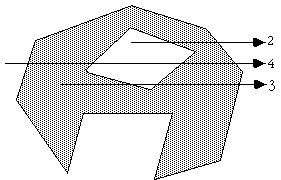
The following C function returns INSIDE or OUTSIDE indicating the status of a point P with respect to a polygon with N points.

#define MIN(x,y) (x < y ? x : y)
#define MAX(x,y) (x > y ? x : y)
#define INSIDE 0
#define OUTSIDE 1

typedef struct {
   double x,y;
} Point;

int InsidePolygon(Point *polygon,int N,Point p)
{
  int counter = 0;
  int i;
  double xinters;
  Point p1,p2;

  p1 = polygon[0];
  for (i=1;i<=N;i++) {
    p2 = polygon[i % N];
    if (p.y > MIN(p1.y,p2.y)) {
      if (p.y <= MAX(p1.y,p2.y)) {
        if (p.x <= MAX(p1.x,p2.x)) {
          if (p1.y != p2.y) {
            xinters = (p.y-p1.y)*(p2.x-p1.x)/(p2.y-p1.y)+p1.x;
            if (p1.x == p2.x || p.x <= xinters)
              counter++;
          }
        }
      }
    }
    p1 = p2;
  }

  if (counter % 2 == 0)
    return(OUTSIDE);
  else
    return(INSIDE);
}

The following code is by Randolph Franklin, it returns 1 for interior points and 0 for exterior points.

    int pnpoly(int npol, float *xp, float *yp, float x, float y)
    {
      int i, j, c = 0;
      for (i = 0, j = npol-1; i < npol; j = i++) {
        if ((((yp[i] <= y) && (y < yp[j])) ||
             ((yp[j] <= y) && (y < yp[i]))) &&
            (x < (xp[j] - xp[i]) * (y - yp[i]) / (yp[j] - yp[i]) + xp[i]))
          c = !c;
      }
      return c;
    }

Contribution by Alexander Motrichuk:

//SOLUTION #1 (2D) - Redesigned

#define MIN(x,y) (x < y ? x : y)
#define MAX(x,y) (x > y ? x : y)

#define INSIDE    1
#define OUTSIDE   0

struct Point
{
    Point() : x(.), y(.) {};

    Point(double x1, double y1) : x(x1), y(y1) {};

    bool operator==(const Point& _right)
    {
        return x == _right.x && y == _right.y;
    };

    double x, y;
};

//horizintal left cross over direction algorithm
//-----------------------------------------------
//  bound   |   value that will be returned only if (p) lies on the bound or vertex
int InsidePolygon(Point* polygon, int N, Point p, int bound)
{
    //cross points count of x
    int __count = ;

    //neighbour bound vertices
    Point p1, p2;

    //left vertex
    p1 = polygon[];

    //check all rays
    for(int i = ; i <= N; ++i)
    {
        //point is an vertex
        if(p == p1) return bound;

        //right vertex
        p2 = polygon[i % N];

        //ray is outside of our interests
        if(p.y < MIN(p1.y, p2.y) || p.y > MAX(p1.y, p2.y))
        {
            //next ray left point
            p1 = p2; continue;
        }

        //ray is crossing over by the algorithm (common part of)
        if(p.y > MIN(p1.y, p2.y) && p.y < MAX(p1.y, p2.y))
        {
            //x is before of ray
            if(p.x <= MAX(p1.x, p2.x))
            {
                //overlies on a horizontal ray
                if(p1.y == p2.y && p.x >= MIN(p1.x, p2.x)) return bound;

                //ray is vertical
                if(p1.x == p2.x)
                {
                    //overlies on a ray
                    if(p1.x == p.x) return bound;
                    //before ray
                    else ++__count;
                }

                //cross point on the left side
                else
                {
                    //cross point of x
                    double xinters = (p.y - p1.y) * (p2.x - p1.x) / (p2.y - p1.y) + p1.x;

                    //overlies on a ray
                    if(fabs(p.x - xinters) < __DBL_EPSILON__) return bound;

                    //before ray
                    if(p.x < xinters) ++__count;
                }
            }
        }
        //special case when ray is crossing through the vertex
        else
        {
            //p crossing over p2
            if(p.y == p2.y && p.x <= p2.x)
            {
                //next vertex
                const Point& p3 = polygon[(i+) % N];

                //p.y lies between p1.y & p3.y
                if(p.y >= MIN(p1.y, p3.y) && p.y <= MAX(p1.y, p3.y))
                {
                    ++__count;
                }
                else
                {
                    __count += ;
                }
            }
        }

        //next ray left point
        p1 = p2;
    }

    //EVEN
    if(__count %  == ) return(OUTSIDE);
    //ODD
    else return(INSIDE);
}

Quote: "For most of the algorithms above there is a pathological case if the point being queried lies exactly on a vertex. The easiest way to cope with this is to test that as a separate process and make your own decision as to whether you want to consider them inside or outside."

Contribution in VBA by Giuseppe Iaria:

'---------------------------------------------------------------------------------------------------------
'************************************ Function InsidePolygon *************************************
'---------------------------------------------------------------------------------------------------------
'VBA implementation of the theory provided by Paul Bourke (http://paulbourke.net/geometry/polygonmesh/)
'author: ing. Giuseppe Iaria - rev. 20/08/2014
'---------------------------------------------------------------------------------------------------------
'The function is based on Solution 1 (2D)
'The function determines if a point P lies inside or outside a Polygon, returning "True" or "False"
'The points are defined through the user-defined type "Point"
'The Polygon is an array of points, each being a user-defined type "Point"
'The Polygon is implemented assuming a "Base 1" condition, so the "Option Base 1" statement is required
'The optional argument "OnPolygonBorder" deals with these special cases:
' - P lies on a vertex of the Polygon
' - P lies on a line segment of the Polygon
'If omitted or passed as "False", and a special case occurs, then the function returns "False"
'If passed as "True", and a special case occurs, then the function returns "True"
'Auxiliary functions used:
' - DistancePointSegment: determines the distance between a point and a line segment
' - Distance2Point: determines the distance between two points
'Both the auxiliary functions have been developed on:
' - the theory by Paul Bourke (http://paulbourke.net/geometry/pointlineplane/)
' - an original VBA code by Brandon Crosby (http://paulbourke.net/geometry/pointlineplane/source.vba)
'---------------------------------------------------------------------------------------------------------

Option Base 

Public Type Point
    x As Double
    y As Double
End Type

Public Function InsidePolygon(Polygon() As Point, P As Point, Optional ByVal OnPolygonBorder As Boolean) As Boolean
Dim counter As Integer, i As Integer, ip1 As Integer
Dim xInters As Double, dist As Double
Const EPS As Single = 0.0001
'Check if the point lies on a polygon's vertex or line segment
For i =  To UBound(Polygon)
    ip1 = i Mod UBound(Polygon) +
    dist = DistancePointSegment(P, Polygon(i), Polygon(ip1))
    If dist < EPS Then
        If OnPolygonBorder Then
            InsidePolygon = True
            Else
            InsidePolygon = False
        End If
        Exit Function
    End If
    Next i
'Determine the numbers of intersection between the orizzontal ray from point and polygon
For i =  To UBound(Polygon)
    ip1 = i Mod UBound(Polygon) +
    If P.y > IIf(Polygon(i).y < Polygon(ip1).y, Polygon(i).y, Polygon(ip1).y) Then
        If P.y <= IIf(Polygon(i).y > Polygon(ip1).y, Polygon(i).y, Polygon(ip1).y) Then
            If P.x <= IIf(Polygon(i).x > Polygon(ip1).x, Polygon(i).x, Polygon(ip1).x) Then
                If Polygon(i).y <> Polygon(ip1).y Then
                    xInters = Polygon(i).x + (Polygon(ip1).x - Polygon(i).x) * (P.y - Polygon(i).y) / (Polygon(ip1).y - Polygon(i).y)
                    If (Polygon(i).x = Polygon(ip1).x) Or (P.x <= xInters) Then counter = counter +
                End If
            End If
        End If
    End If
    Next i
If counter Mod  =  Then InsidePolygon = False Else InsidePolygon = True
End Function

Private Function DistancePointSegment(P As Point, P1 As Point, P2 As Point) As Double
Dim LineMag As Double, u As Double
Dim d1 As Double, d2 As Double
Dim Pint As Point
Const EPS As Single = 0.0001
LineMag = Distance2Point(P1, P2)
If LineMag < EPS Then Exit Function
u = (((P.x - P1.x) * (P2.x - P1.x)) + ((P.y - P1.y) * (P2.y - P1.y))) / LineMag ^
If u <  Or u >  Then
    d1 = Distance2Point(P, P1)
    d2 = Distance2Point(P, P2)
    If d1 > d2 Then DistancePointSegment = d2 Else DistancePointSegment = d1
    Else
    Pint.x = P1.x + u * (P2.x - P1.x)
    Pint.y = P1.y + u * (P2.y - P1.y)
    DistancePointSegment = Distance2Point(P, Pint)
End If
End Function

Private Function Distance2Point(P1 As Point, P2 As Point) As Double
Distance2Point = Sqr((P2.x - P1.x) ^  + (P2.y - P1.y) ^ )
End Function

Contribution written in c# by Jerry Knauss:

public static bool Contains( Point[] points, Point p )
{
   bool result = false;

   for( int i = ; i < points.Length - ; i++ )
   {
      if( ( ( ( points[ i +  ].Y <= p.Y ) && ( p.Y < points[ i ].Y ) ) || ( ( points[ i ].Y <= p.Y ) && ( p.Y < points[ i +  ].Y ) ) ) && ( p.X < ( points[ i ].X - points[ i +  ].X ) * ( p.Y - points[ i +  ].Y ) / ( points[ i ].Y - points[ i +  ].Y ) + points[ i +  ].X ) )
      {
         result = !result;
      }
   }
   return result;
}

Solution 2 (2D)

Another solution forwarded by Philippe Reverdy is to compute the sum of the angles made between the test point and each pair of points making up the polygon. If this sum is 2pi then the point is an interior point, if 0 then the point is an exterior point. This also works for polygons with holes given the polygon is defined with a path made up of coincident edges into and out of the hole as is common practice in many CAD packages.

The inside/outside test might then be defined in C as

typedef struct {
   int h,v;
} Point;

int InsidePolygon(Point *polygon,int n,Point p)
{
   int i;
   double angle=0;
   Point p1,p2;

   for (i=0;i<n;i++) {
      p1.h = polygon[i].h - p.h;
      p1.v = polygon[i].v - p.v;
      p2.h = polygon[(i+1)%n].h - p.h;
      p2.v = polygon[(i+1)%n].v - p.v;
      angle += Angle2D(p1.h,p1.v,p2.h,p2.v);
   }

   if (ABS(angle) < PI)
      return(FALSE);
   else
      return(TRUE);
}

/*
   Return the angle between two vectors on a plane
   The angle is from vector 1 to vector 2, positive anticlockwise
   The result is between -pi -> pi
*/
double Angle2D(double x1, double y1, double x2, double y2)
{
   double dtheta,theta1,theta2;

   theta1 = atan2(y1,x1);
   theta2 = atan2(y2,x2);
   dtheta = theta2 - theta1;
   while (dtheta > PI)
      dtheta -= TWOPI;
   while (dtheta < -PI)
      dtheta += TWOPI;

   return(dtheta);
}

Solution 3 (2D)

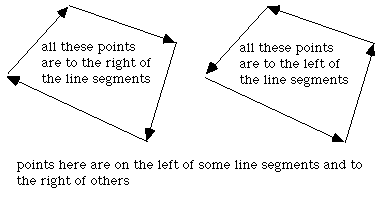
There are other solutions to this problem for polygons with special attributes. If the polygon is convex then one can consider the polygon as a "path" from the first vertex. A point is on the interior of this polygons if it is always on the same side of all the line segments making up the path.

Given a line segment between P₀ (x₀,y₀) and P₁ (x₁,y₁), another point P (x,y) has the following relationship to the line segment.

Compute

(y - y₀) (x₁ - x₀) - (x - x₀) (y₁ - y₀)

if it is less than 0 then P is to the right of the line segment, if greater than 0 it is to the left, if equal to 0 then it lies on the line segment.

Solution 4 (3D)

This solution was motivated by solution 2 and correspondence with Reinier van Vliet and Remco Lam. To determine whether a point is on the interior of a convex polygon in 3D one might be tempted to first determine whether the point is on the plane, then determine it's interior status. Both of these can be accomplished at once by computing the sum of the angles between the test point (q below) and every pair of edge points p[i]->p[i+1]. This sum will only be 2pi if both the point is on the plane of the polygon AND on the interior. The angle sum will tend to 0 the further away from the polygon point q becomes.

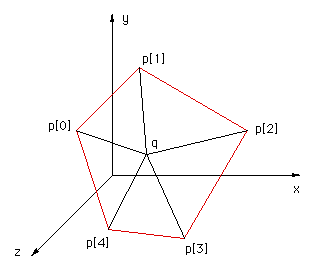The following code snippet returns the angle sum between the test point q and all the vertex pairs. Note that the angle sum is returned in radians.

typedef struct {
   double x,y,z;
} XYZ;
#define EPSILON  0.0000001
#define MODULUS(p) (sqrt(p.x*p.x + p.y*p.y + p.z*p.z))
#define TWOPI 6.283185307179586476925287
#define RTOD 57.2957795

double CalcAngleSum(XYZ q,XYZ *p,int n)
{
   int i;
   double m1,m2;
   double anglesum=0,costheta;
   XYZ p1,p2;

   for (i=0;i<n;i++) {

      p1.x = p[i].x - q.x;
      p1.y = p[i].y - q.y;
      p1.z = p[i].z - q.z;
      p2.x = p[(i+1)%n].x - q.x;
      p2.y = p[(i+1)%n].y - q.y;
      p2.z = p[(i+1)%n].z - q.z;

      m1 = MODULUS(p1);
      m2 = MODULUS(p2);
      if (m1*m2 <= EPSILON)
         return(TWOPI); /* We are on a node, consider this inside */
      else
         costheta = (p1.x*p2.x + p1.y*p2.y + p1.z*p2.z) / (m1*m2);

      anglesum += acos(costheta);
   }
   return(anglesum);
}

Note

For most of the algorithms above there is a pathological case if the point being queries lies exactly on a vertex. The easiest way to cope with this is to test that as a separate process and make your own decision as to whether you want to consider them inside or outside.