LCA和RMQ

下面写提供几个学习LCA和RMQ的博客，都很通熟易懂

http://dongxicheng.org/structure/lca-rmq/

这个应该是讲得最好的，且博主还有很多其他文章，可以读读，感觉认真读了这篇，都不太需要看别的资料了，百度和谷歌搜索的第一位都是他，好东西大家一起学习

http://scturtle.is-programmer.com/posts/30055

这个博客讲LCA的Tarjan算法个人觉得是比较好的，我看这篇文章，看了1个小时就搞懂了LCA的Tarjan，谢谢博主。可以认真阅读，并且看懂里面附带的那个图

其余的博客，就请百度和谷歌了，能找到很多，都很好

一：LCA和RMQ相互转化

往往都只是提到了LCA可以转化为RMQ去求解，其实RMQ也能转化为LCA去求解，RMQ怎么转LCA，可以看2007年的国家队论文，里面有介绍，非常好懂。不过个人觉得，RMQ转LCA，可以学习这个思想，但是实际应用中最好不要，多此一举的感觉，求解RMQ的算法很多，不必要用LCA去求解

所以下面讲讲LCA转RMQ的实现方法（只讲实现方法，具体的原理不讲，可以看书百度，不过看了实现过程，原理大概也懂了）

LCA转RMQ算法是一个在线算法：先用时间去做预处理，然后每读入一个询问，就用很短的时间去回答它，即”问一个答一个，回答时间很短“

预备知识：LCA转为RMQ后，几乎是裸的RMQ问题，RMQ问题，这里推荐ST算法求解，如果不懂ST算法，先学习一下

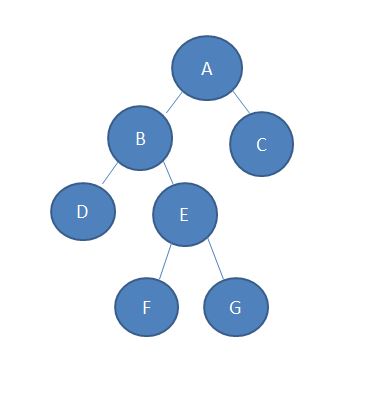
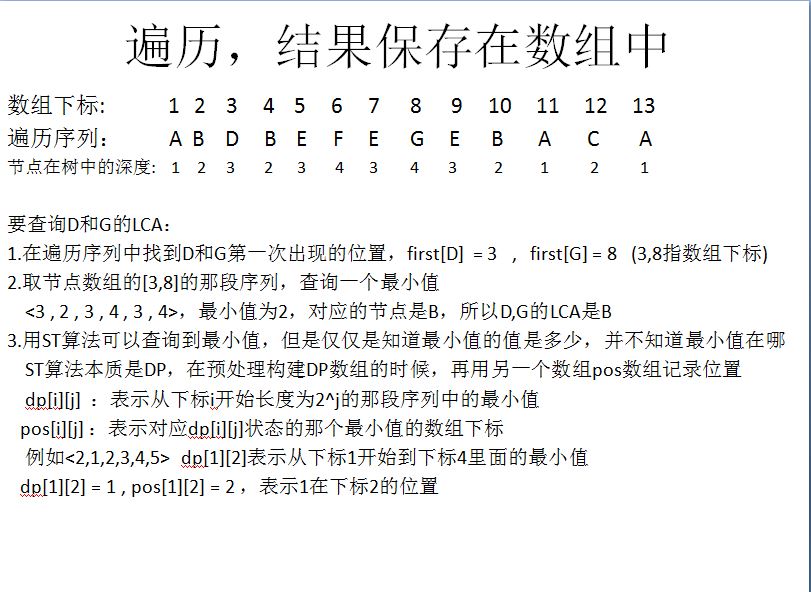
二：LCA的Tarjan算法

Tarjan算法是个离线算法：即先把所有询问保存下来，但是不回答（也回答不了），重新组织这些询问，然后再回答，但是回答的顺序，不一定是询问的顺序，即”一口气问完，处理完，再一口气回答“。如果一定要你按照询问的顺序得出答案，那么还要稍微处理一下

说说感悟：很多人说Tarjan算法强调递推的性质，我个人感觉说递推不够直接，应该说是强调时间，先后顺序。学了Tarjan几个算法，都有时间戳这个概念，这个算法里没强调这个，但是有这个意思。它定义了一个概念，什么叫处理完的节点，就是这个节点被访问了且它下面的所有子树的所有节点都被访问了，就认为这个节点是处理完了，由于是前序遍历这棵树，所以节点被处理，是有个先后顺序的，我们知道Tarjan在处理完一个节点后，就看看这个节点涉及了哪些询问，看看呗询问的另一个点是否也是被处理完的，如果另一个点也是被处理完的，那么这个询问可以被回答，否则，现在还不能回答，要等下再回答，什么时候回答，就是等到那个节点也被处理完的时候。

说说代码实现上的问题

如果理解了Tarjan，写出那个核心的dfs遍历反而不难，有时候纠结的是怎么保存询问的答案，并且按照询问的顺序，还原出答案

首先，我们是先把询问拆成两份，例如询问x和y的lca，拆成x和y的lca ， y和x的lca，两者是完全相同的，等价的

对于一系列询问

1 2

1 3

2 3

3 4

变为

1 2

2 1

1 3

3 1

2 3

3 2

3 4

4 3

然后保存，保存方式是用邻接表（个人感觉这种方法比较好，可以用上位运算，记录的东西也比较少）。保存在一个表中，表的下标从0开始标号

对已表中的第k项，例如 2 3 ， 那么k^1项和k项的LCA是相同的，所以就可以保存  a[k].lca = a[k^1].lca = ans

最后注意一点，Tarjan的伪代码可以很好帮助理解算法本质，注意里面一个并查集合并的操作Union(x,y)。这个Union(x,y)有好多写法，其中最简单的就是一个语句（个人推荐这种），这个Union的写法会稍微影响到dfs函数里面的写法（不影响算法本质，只是影响写法）

具体看模板

三、代码示例

LCA转RMQ的模板

const int N = 40010;
const int M = 25;

int _pow[M];     //事先保存2^x，不必重复计算
int head[N];     //邻接表表头
int ver[2*N];    //保存遍历的节点序列，长度为2n-1，从下标1开始保存
int R[2*N];      //和遍历序列对应的节点深度数组，长度为2n-1，从下标1开始保存
int first[N];    //每个节点在遍历序列中第一次出现的位置
int dir[N];      //保存每个点到树根的距离，很多问题中树边都有权值，会询问两点间的距离，如果树边没权值，相当于权值为1
int dp[2*N][M];  //这个数组记得开到2*N，因为遍历后序列长度为2*n-1
bool vis[N];     //遍历时的标记数组
int tot;
struct edge //保存边，数组大小至少为2*n
{
    int u,v,w,next;
}e[2*N];

void dfs(int u ,int dep) //遍历树，过程中顺便做了好多事情
{
    vis[u] = true; ver[++tot] = u; first[u] = tot; R[tot] = dep;
    for(int k=head[u]; k!=-1; k=e[k].next)
        if( !vis[e[k].v] )
        {
            int v = e[k].v , w = e[k].w;
            dir[v] = dir[u] + w;
            dfs(v,dep+1);
            ver[++tot] = u; R[tot] = dep;
        }
}

int RMQ(int x ,int y) //这个询问仅仅是返回一个位置，即LCA所在序列数组的位置，ver[res]才是LCA的标号
{
    int K = (int)(log((double)(y-x+1)) / log(2.0));
    int a = dp[x][K] , b = dp[y-_pow[K]+1][K];
    if(R[a] < R[b]) return a;
    else            return b;
}

int LCA(int u ,int v)  //返回点u和点v的LCA
{
    int x = first[u] , y = first[v];
    if(x > y) swap(x,y);
    int res = RMQ(x,y);
    return ver[res];
}

//  lcaxy = LCA(x,y);
//  lcaab = LCA(a,b);

Tarjand的伪代码

void Tarjan(int u)
{
    vis[u] = true;
    Make-Set(u); //以点u自己为代表元素建立一个集合，此时集合也只有它自己一个元素
    ance[Find(u)] = u; //记录点u所在的那个集合的祖先是u自己，其实此时还是只有它自己
    for(u的所有儿子v)
        if(该儿子v没有被访问)
        {
            Tarjan(v);
            Union(u,v); //将儿子v所在集合并在点u所在的集合，点u已经是集合的代表元素
            ance[Find(u)] = u; //确保点u所在的集合的祖先是u自己
        }
    colour[u] = true;   //这个点u认为已经处理完
    for(u的所有儿子v)
        if( colour[v] )  //儿子v也被处理完
            LCA(u,v) = LCA(v,u) = ance[Find(v)];  //两者的LCA此时可以回答了，就是儿子v所在的集合的祖先
}

Tarjan模板

using namespace std;
const int N = 40010;
const int M = 410;

int head[N];            //树边邻接表的表头
int __head[N];          //保存询问的邻接表的表头
struct edge{            //保存边
    int u,v,w,next;
}e[2*N];
struct ask{            //保存询问
    int u,v,lca,next;
}ea[M];
int dir[N];              //保存点到树根的距离
int fa[N];               //并查集，保存集合的代表元素
int ance[N];             //保存集合的组合，注意对象是集合而不是元素
bool vis[N];             //遍历时的标记数组

inline void add_edge(int u,int v,int w,int &k) //保存边
{
    e[k].u = u; e[k].v = v; e[k].w = w;
    e[k].next = head[u]; head[u] = k++;
    u = u^v; v = u^v; u = u^v;
    e[k].u = u; e[k].v = v; e[k].w = w;
    e[k].next = head[u]; head[u] = k++;
}

inline void add_ask(int u ,int v ,int &k) //保存询问
{
    ea[k].u = u; ea[k].v = v; ea[k].lca = -1;
    ea[k].next = __head[u]; __head[u] = k++;
    u = u^v; v = u^v; u = u^v;
    ea[k].u = u; ea[k].v = v; ea[k].lca = -1;
    ea[k].next = __head[u]; __head[u] = k++;
}

int Find(int x)
{
    return x == fa[x] ? x : fa[x] = Find(fa[x]);
}
void Union(int u ,int v)
{
    fa[v] = fa[u];  //可写为  fa[Find(v)] = fa[u];
}

void Tarjan(int u)
{
    vis[u] = true;
    ance[u] = fa[u] = u; //可写为 ance[Find(u)] = fa[u] = u;
    for(int k=head[u]; k!=-1; k=e[k].next)
        if( !vis[e[k].v] )
        {
            int v = e[k].v , w = e[k].w;
            dir[v] = dir[u] + w;
            Tarjan(v);
            Union(u,v);
            ance[Find(u)] = u;  //可写为ance[u] = u;  //甚至不要这个语句都行
        }
    for(int k=__head[u]; k!=-1; k=ea[k].next)
        if( vis[ea[k].v] )
        {
            int v = ea[k].v;
            ea[k].lca = ea[k^1].lca = ance[Find(v)];
        }
}

int main()
{
    //.............省略..............
    memset(head,-1,sizeof(head));
    memset(__head,-1,sizeof(__head));
    tot = 0;
    for(int i=1; i<n; i++)  //建树
    {
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        add_edge(u,v,w,tot);
    }
    tot = 0;
    for(int i=0; i<q; i++) //拆开保存询问
    {
        int u,v;
        scanf("%d%d",&u,&v);
        add_ask(u,v,tot);
    }
    memset(vis,0,sizeof(vis));
    dir[1] = 0;
    Tarjan(1);
    for(int i=0; i<q; i++)
    {
        int s = i * 2 , u = ea[s].u , v = ea[s].v , lca = ea[s].lca;
        //已经按顺序取出了询问和答案，lca = LCA(u,v)
    }
    return 0;
}

Reference：

LCA和RMQ的一些事情