51nod 1100 斜率最大
可以用三个点简单证明斜率最大的直线两个点!
#include <bits/stdc++.h>#define MAXN 10010using namespace std;struct Node{int x, y, number;}gg[MAXN];bool cmp(Node a, Node b){return a.x<b.x;}int main(void){std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);int n;cin >> n;for(int i=0; i<n; i++){cin >> gg[i].x >> gg[i].y;gg[i].number=i+1;}sort(gg, gg+n, cmp);queue<int> node1, node2;double cnt=0, cc=0;for(int i=1; i<n; i++){cnt=(gg[i].y-gg[i-1].y)*1.0/(gg[i].x-gg[i-1].x);if(cnt>cc){cc=cnt;while(!node1.empty()){node1.pop();}while(!node2.empty()){node2.pop();}node1.push(gg[i-1].number);node2.push(gg[i].number);}else if(cnt==cc){node1.push(gg[i-1].number);node2.push(gg[i].number);}}while(!node1.empty()){cout << node1.front() << " " << node2.front() << endl;node1.pop();node2.pop();}return 0;}
51nod 1100 斜率最大的更多相关文章
- 51 Nod 1100 斜率最大
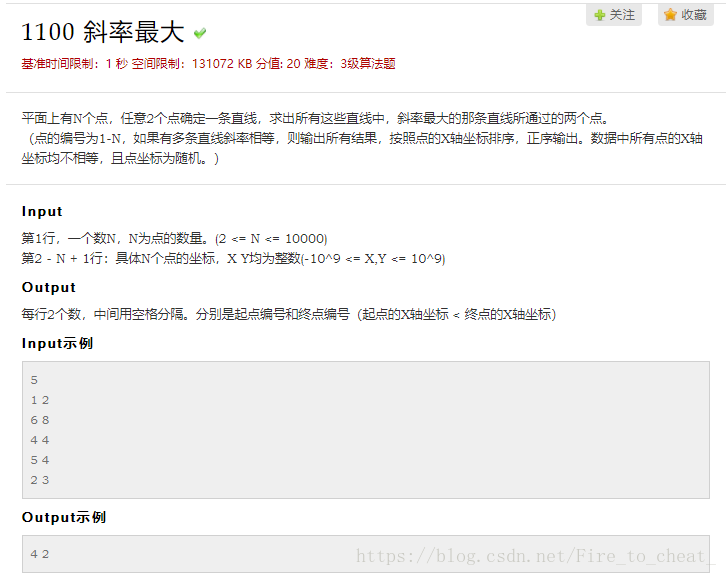
1100 斜率最大 基准时间限制:1 秒 空间限制:131072 KB 分值: 20 难度:3级算法题 收藏 关注 平面上有N个点,任意2个点确定一条直线,求出所有这些直线中,斜率最大的那条直线 ...
- 【51nod 1100】斜率最大
Description 平面上有N个点,任意2个点确定一条直线,求出所有这些直线中,斜率最大的那条直线所通过的两个点. (点的编号为1-N,如果有多条直线斜率相等,则输出所有结果,按照点的X轴坐标 ...
- 51Nod P1100 斜率最大
传送门: https://www.51nod.com/onlineJudge/questionCode.html#!problemId=1100 由于2 <= N <= 10000, 所以 ...
- 51Nod - 1107 斜率小于0的连线数量
二维平面上N个点之间共有C(n,2)条连线.求这C(n,2)条线中斜率小于0的线的数量. 二维平面上的一个点,根据对应的X Y坐标可以表示为(X,Y).例如:(2,3) (3,4) (1,5) (4, ...
- 【51NOD】斜率最大
[题解]通过画图易得结论:最大斜率一定出现在相邻两点之间. #include<cstdio> #include<algorithm> #include<cstring&g ...
- 51nod 1107 斜率小于零连线数量 特调逆序数
逆序数的神题.... 居然是逆序数 居然用逆序数过的 提示...按照X从小到大排列,之后统计Y的逆序数... 之后,得到的答案就是传说中的解(斜率小于零) #include<bits/stdc+ ...
- 51NOD——N 1107 斜率小于0的连线数量
https://www.51nod.com/onlineJudge/questionCode.html#!problemId=1107 基准时间限制:1 秒 空间限制:131072 KB 分值: 40 ...
- 51nod 1451 合法三角形 判斜率去重,时间复杂度O(n^2)
题目: 这题我WA了3次,那3次是用向量求角度去重算的,不知道错在哪了,不得不换思路. 第4次用斜率去重一次就过了. 注意:n定义成long long,不然求C(3,n)时会溢出. 代码: #incl ...
- 51nod 1488 帕斯卡小三角 斜率优化
思路:斜率优化 提交:\(2\)次 错因:二分写挂 题解: 首先观察可知, 对于点\(f(X,Y)\),一定是由某个点\((1,p)\),先向下走,再向右下走. 并且有个显然的性质,若从\((1,p) ...
随机推荐
- crm使用soap删除下拉框
//C# 代码: //DeleteOptionSetRequest request = new DeleteOptionSetRequest(); //request.Name = "new ...
- BZOJ 1005 明明的烦恼 Prufer序列+组合数学+高精度
题目大意:给定一棵n个节点的树的节点的度数.当中一些度数无限制,求能够生成多少种树 Prufer序列 把一棵树进行下面操作: 1.找到编号最小的叶节点.删除这个节点,然后与这个叶节点相连的点计入序列 ...
- Asp.net MVC 简单分页 自做简单分页
Asp.net MVC 简单分页: public static string Pager(int page,int pageSize,int total) { ...
- Android项目之HomeHealth基础学习2:Service
一. Service简单介绍 Service是android 系统中的四大组件之中的一个(Activity.Service.BroadcastReceiver.ContentProvider),它跟A ...
- linux【第六篇】用户和用户管理及定时任务复习
定时任务复习 1.什么是定时任务? 2.如何编辑查看定时任务(配置文件位置?),语法的特殊字符意义是什么?- * , / 3.书写定时任务有哪些要领? 4.生产如何调试定时任务 5.生产场景配置定时任 ...
- android 怎样将主菜单图标改成按安装时间排序
1. 在 LauncherModel.java 中增加例如以下代码, 假设是KK Launcher3 ApplicationInfo要替换为AppInfo public static final Co ...
- 【iOS系列】-使用CAGradientLayer设置渐变色
有时候iOS开发中需要使用到渐变色,来给图片或者view盖上一层,使其显示效果更好,我们这里使用的CAGradientLayer来设置渐变色 要实现的效果如下: Demo地址---下载 // 创建渐变 ...
- Android数据与服务器交互的GET,POST,HTTPGET,HTTPPOST的使用
Android有这几种方式,可以提交数据到服务器,他们是怎么使用的呢,这里我们来探讨一下. 这里的例子用的都是提交客户端的用户名及密码,同时本节用到的StreamTools.readInputStre ...
- 设计模式-(6)适配器 (swift版)
用来解决接口适配问题的三种模式:适配器模式,桥接模式,外观模式. 一,概念 适配器模式,将一个类的结构转换成用户希望的另一个接口,使得原本接口不兼容的类能在一起工作.换句话说,适配器模式就是链接两种不 ...
- CRM2011部署问题小结
1 CRM2011部署当插件太多,并且文件太多的时候选择硬盘部署 2 在生产环境这样复杂的CRM2011部署环境的时候弄清楚每台CRM服务器的结构是很重要的弟一步 3 一定要注意DMZ区和内网隔离的, ...