SPFA 算法详解( 强大图解，不会都难！) （转）

适用范围：给定的图存在负权边，这时类似Dijkstra等算法便没有了用武之地，而Bellman-Ford算法的复杂度又过高，SPFA算法便 派上用场了。 我们约定有向加权图G不存在负权回路，即最短路径一定存在。当然，我们可以在执行该算法前做一次拓扑排序，以判断是否存在负权回路，但这不是我们讨论的重 点。

算法思想：我们用数组d记录每个结点的最短路径估计值，用邻接表来存储图G。我们采取的方法是动态逼近法：设立一个先进先出的队列用来保存待优化的
结点，优化时每次取出队首结点u，并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作，如果v点的最短路径估计值有所调整，且v点不在
当前的队列中，就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作，直至队列空为止

期望的时间复杂度O(ke)， 其中k为所有顶点进队的平均次数，可以证明k一般小于等于2。

实现方法：

　　建立一个队列，初始时队列里只有起始点，再建立一个表格记录起始点到所有点的最短路径（该表格的初始值要赋为极大值，该点到他本身的路径赋为
0）。然后执行松弛操作，用队列里有的点作为起始点去刷新到所有点的最短路，如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列
为空。

判断有无负环：
　　如果某个点进入队列的次数超过N次则存在负环（SPFA无法处理带负环的图）

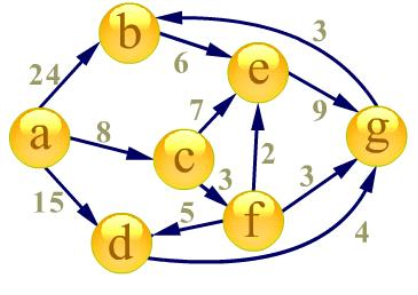
首先建立起始点a到其余各点的
最短路径表格

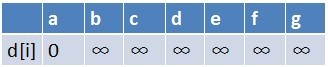
首先源点a入队，当队列非空时：
　１、队首元素（a）出队，对以a为起始点的所有边的终点依次进行松弛操作（此处有b,c,d三个点），此时路径表格状态为：

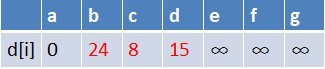
在松弛时三个点的最短路径估值变小了，而这些点队列中都没有出现，这些点
需要入队，此时，队列中新入队了三个结点b,c,d

队首元素b点出队，对以b为起始点的所有边的终点依次进行松弛操作（此处只有e点），此时路径表格状态为：

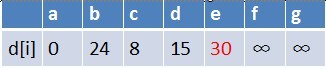
在最短路径表中，e的最短路径估值也变小了，e在队列中不存在，因此e也要
入队，此时队列中的元素为c，d，e

队首元素c点出队，对以c为起始点的所有边的终点依次进行松弛操作（此处有e,f两个点），此时路径表格状态为：

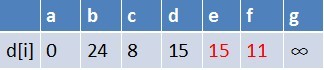
在最短路径表中，e，f的最短路径估值变小了，e在队列中存在，f不存在。因此
e不用入队了，f要入队，此时队列中的元素为d，e，f

队首元素d点出队，对以d为起始点的所有边的终点依次进行松弛操作（此处只有g这个点），此时路径表格状态为：

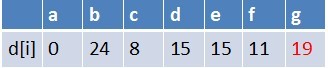
在最短路径表中，g的最短路径估值没有变小（松弛不成功），没有新结点入队，队列中元素为f，g

队首元素f点出队，对以f为起始点的所有边的终点依次进行松弛操作（此处有d，e，g三个点），此时路径表格状态为：

在最短路径表中，e，g的最短路径估值又变小，队列中无e点，e入队，队列中存在g这个点，g不用入队，此时队列中元素为g，e

队首元素g点出队，对以g为起始点的所有边的终点依次进行松弛操作（此处只有b点），此时路径表格状态为：

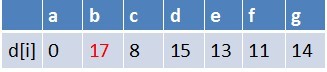
在最短路径表中，b的最短路径估值又变小，队列中无b点，b入队，此时队列中元素为e，b
队首元素e点出队，对以e为起始点的所有边的终点依次进行松弛操作（此处只有g这个点），此时路径表格状态为：

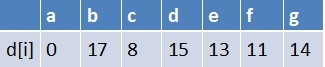
在最短路径表中，g的最短路径估值没变化（松弛不成功），此时队列中元素为b

队首元素b点出队，对以b为起始点的所有边的终点依次进行松弛操作（此处只有e这个点），此时路径表格状态为：

在最短路径表中，e的最短路径估值没变化（松弛不成功），此时队列为空了

最终a到g的最短路径为１４

program：

#include<cstdio>
using namespace std;
struct node
{int x;
 int value;
 int next;
};
node e[60000];
int visited[1505],dis[1505],st[1505],queue[1000];
int main()
{
  int n,m,u,v,w,start,h,r,cur;
  freopen("c.in","r",stdin);
  freopen("c.out","w",stdout);
  while(scanf("%d%d",&n,&m)!=EOF)
  {
    for(int i=1;i<=1500;i++)
      {visited[i]=0;
       dis[i]=-1;
       st[i]=-1;  //这个初始化给下边那个while循环带来影响
      }
 
   for(int i=1;i<=m;i++)
      {
       scanf("%d%d%d\n",&u,&v,&w);    
       e[i].x=v;            //记录后继节点    相当于链表中的创建一个节点，并使得数据域先记录
       e[i].value=w;
       e[i].next=st[u];     //记录顶点节点的某一个边表节点的下标，相当于在链表中吧该边表节点的next指针先指向他的后继边表节点
       st[u]=i;                //把该顶点的指针指向边表节点，相当于链表中的插入中，头结点的指针改变
      }
    start=1;
    visited[start]=1;
    dis[start]=0;
    h=0;
    r=1;
    queue[r]=start;
    while(h!=r)
     {

h=(h+1)%1000;
      cur=queue[h];
      int tmp=st[cur];
      visited[cur]=0;

while(tmp!=-1)
        {
            if (dis[e[tmp].x]<dis[cur]+e[tmp].value)            //改成大于号才对
            {
                   dis[e[tmp].x]=dis[cur]+e[tmp].value;
                    if(visited[e[tmp].x]==0)
                      {

visited[e[tmp].x]=1;
                           r=(r+1)%1000;
                            queue[r]=e[tmp].x;
                       }
            }
         tmp=e[tmp].next;     
        }
     }
    printf("%d\n",dis[n]);
  }
  return 0;  
}