【组合数+Lucas定理模板】HDU 3037 Saving

acm.hdu.edu.cn/showproblem.php?pid=3037

【题意】

• m个松果，n棵树
• 求把最多m个松果分配到最多n棵树的方案数
• 方案数有可能很大，模素数p
• 1 <= n, m <= 1000000000, 1 < p < 100000

【思路】

• 答案为C(n+m,m)%p

• 对于C(n, m) mod p。这里的n，m，p（p为素数）都很大的情况。就不能再用C(n, m) = C(n - 1，m) + C(n - 1, m - 1)的公式递推了。这里用到Lucas定理。

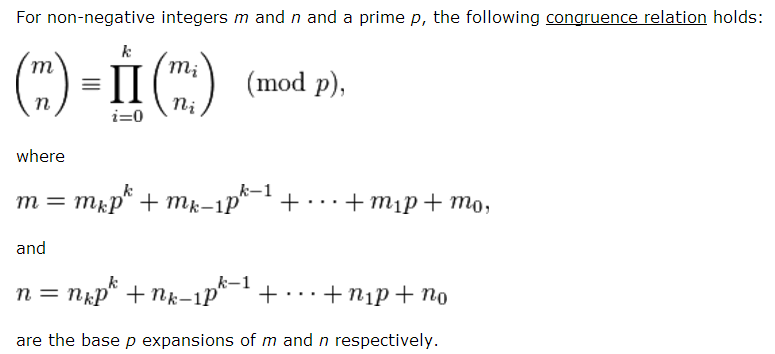
• 下面证明为什么答案是C(n+m,m):

• 把i个松果分配到最多n棵树的方案数是:C(i+n-1,i)（相当于x1+x2+......+xn=i的解的个数，用插板法,插n-1个板，共i+n-1个位置选i个1,因为xi可能是0，所以满足最多n棵树）

• 现在就需要求不大于m的，相当于对i = 0,1...,m对C(n+i-1,i)求和，根据公式C(n,k) = C(n-1,k)+C(n-1,k-1)得

  C(n-1,0)+C(n,1)+...+C(n+m-1,m)

  = C(n,0)+C(n,1)+C(n+1,2)+...+C(n+m-1,m)

  = C(n+m,m)

【AC】

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;

 ll n,m,p;

 ll fpow(ll x,ll n,ll p)
 {
     ll res=;
     while(n)
     {
         if(n&) res=(res*x)%p;
         x=(x*x)%p;
         n>>=;
     }
     return res;
 }
 ll Comb(ll n,ll m,ll p)
 {
     if(n<m) return ;
     if(n==m) return ;
     m=min(m,n-m);
     ll lm=,ln=;
     for(ll i=;i<m;i++)
     {
         lm=(lm*(m-i))%p;
         ln=(ln*(n-i))%p;
     }
     ll ans=ln*fpow(lm,p-,p)%p;
     return ans;
 }
 ll Lucas(ll n,ll m,ll p)
 {
     ll ans=;
     while(n&&m&&ans)
     {
         ans=(ans*Comb(n%p,m%p,p))%p;
         n/=p;
         m/=p;
     }
     return ans;
 }
 int main()
 {
     int T;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%lld%lld%lld",&n,&m,&p);
         n+=m;
         ll ans=Lucas(n,m,p);
         printf("%lld\n",ans);
     }
     return ;
 } 

Lucas模板