Subsets and Subsets II (回溯，DFS，组合问题)

Given a set of distinct integers, S, return all possible subsets.

Note:

• Elements in a subset must be in non-descending order.
• The solution set must not contain duplicate subsets.

For example,
If S = [1,2,3], a solution is:

[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

该题和Combinations很类似，只不过是k需要从0到size中取值。

class Solution {
private:
    vector<vector<int>> res;
    vector<int> s;
public:
    void tra(int k,int start,int dep,vector<int> temp)
    {
        if(dep==k){
            res.push_back(temp);
            return;
        }
        for(int i=start;i<s.size();++i){
            temp.push_back(s[i]);
            tra(k,i+,dep+,temp);//是i+1，而不是start+1
            temp.erase(temp.end()-);
        }
    }
    vector<vector<int>> subsets(vector<int> &S) {
        s=S;
        sort(s.begin(),s.end());
        vector<int> temp;
        for(int k=;k<=s.size();++k){
            tra(k,,,temp);
        }
        return res;
    }
};

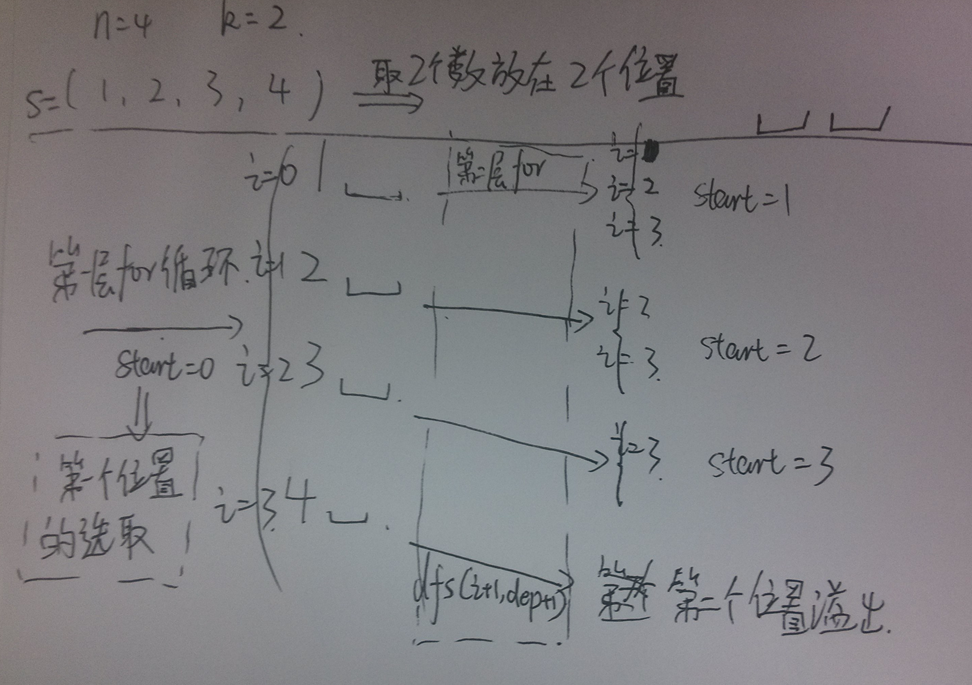
我的分析图：

---

Subsets 2

Given a collection of integers that might contain duplicates, S, return all possible subsets.

Note:

• Elements in a subset must be in non-descending order.
• The solution set must not contain duplicate subsets.

For example,
If S = [1,2,2], a solution is:

[
  [2],
  [1],
  [1,2,2],
  [2,2],
  [1,2],
  []
]

class Solution {
private:
    vector<vector<int>> res;
    vector<int> s;
public:
    void tra(int k,int start,int dep,vector<int> temp)
    {
        if(dep==k){
            for (int i=;i<res.size();++i)
            {
                if(res[i]==temp) return;
            }
            res.push_back(temp);
            return;
        }
        for(int i=start;i<s.size();++i){
            temp.push_back(s[i]);
            tra(k,i+,dep+,temp);
            temp.erase(temp.end()-);
        }
    }
    vector<vector<int>> subsetsWithDup(vector<int> &S) {
        s=S;
        sort(s.begin(),s.end());
        vector<int> temp;
        res.push_back(temp);
        for(int k=;k<=s.size();++k){
            tra(k,,,temp);
        }
        return res;
    }
};