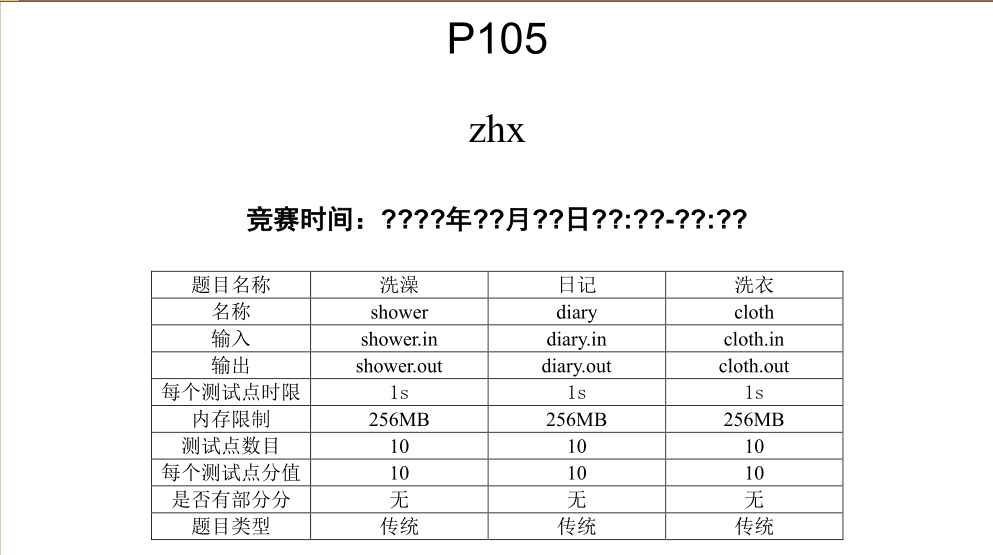
清北考前刷题day2下午好

#include<iostream>
#include<cstdio>
#include<cstring>
#include<stack>

#define N 100007

using namespace std;
char ch[N];
int ans,pos;
stack<char>s;
int main()
{
    freopen("shower.in","r",stdin);
    freopen("shower.out","w",stdout);
    scanf("%s",ch);int len=strlen(ch);
    if(!len){printf("0\n");return ;}
    for(int i=;i<len;i++)
    {
        if(ch[i]==')')
        {
            if(!pos) ++pos,++ans;
            else --pos;
        }
        else ++pos;
    }
    printf("%d\n",ans+pos/);
    return ;
}

日记

/*
前缀和里二分
但枚举的话由于素数在范围里只有大约7*10^4个，2000询问，理论复杂度1.5*10^8电脑跑得比较快比较快是可以过掉的。
*/
#include<iostream>
#include<cstdio>
#include<cstring>

#define ll long long
#define N 1000007

using namespace std;
int T,n,m,k;
int ans,cnt;
int pri[N],tot[N],pos[N];
ll sum[N];
bool no[N];

#define Inline __attribute__( ( optimize ( "-O2" ) ) )

Inline int max(ll a,ll b){return a>b?a:b;}

Inline void prime()
{
    for(int i=;i<=N;i++)
    {
        if(!no[i]) pri[++cnt]=i,sum[cnt]=sum[cnt-]+i,tot[i]++;
        pos[i]=pri[cnt];
        for(int j=;j<=cnt;j++)
        {
            if(i*pri[j]>N) break;
            no[i*pri[j]]=;
            if(!i%pri[j]) break;
        }
    }
    for(int i=;i<=N;i++) tot[i]+=tot[i-];
}

Inline int read()
{
    int x=,f=;char c=getchar();
    while(c>''||c<''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}

Inline int Main()
{
    freopen("diary.in","r",stdin);
    freopen("diary.out","w",stdout);
    prime();T=read();
    while(T--)
    {
        n=read();k=read();ans=-;
        if(tot[n]<k) {printf("-1\n");continue;}
        if(k==) {printf("d\n",pos[n]);continue;}
        for(int i=tot[n];i-k>=;i--)
          if(sum[i]-sum[i-k]<=n) ans=max(ans,sum[i]-sum[i-k]);
        printf("%d\n",ans);
    }
}

int dawn=Main();int main(){};

洗衣

/*
暴力建树,floyed算距离
*/
#include<iostream>
#include<cstdio>
#include<cstring>

using namespace std;
int dis[][][];
int sz[];
int n,m,a,b,c,d,l;

void floyed(int x)
{
    for(int k=;k<sz[x];k++)
      for(int i=;i<sz[x];i++)
        for(int j=;j<sz[x];j++)
        {
            if(i==j || j==k || k==i) continue;
            dis[x][i][j]=min(dis[x][i][j],dis[x][i][k]+dis[x][j][k]);
        }
        int ans=;
        for(int i=;i<sz[x];i++)
          for(int j=i+;j<sz[x];j++)
            ans+=dis[x][i][j];
    printf("%d\n",ans);
}

int main()
{
    memset(dis,/,sizeof dis);
    sz[]=;dis[][][]=;scanf("%d",&m);
    for(int i=;i<=m;i++)
    {
        scanf("%d%d%d%d%d",&a,&b,&c,&d,&l);
        sz[i]=sz[a]+sz[b];
        for(int j=;j<sz[a];j++)
          for(int k=;k<sz[a];k++)
            dis[i][j][k]=dis[i][k][j]=dis[a][j][k];

        for(int j=;j<sz[b];j++)
          for(int k=;k<sz[b];k++)
            dis[i][j+sz[a]][k+sz[a]]=dis[i][k+sz[a]][j+sz[a]]=dis[b][j][k];
        dis[i][c][d+sz[a]]=dis[i][d+sz[a]][c]=l;
        floyed(i);
    }
} 

40暴力

/*
T3
60的数据O(n)求每棵树距离，树形dp。
标算：
考虑拼起来的树答案由三部分组成，假设第一部分为第j颗树，加上一条边连第k棵树。答案F(Ti)=F(Tj)+F(Tk)+j中每个点到k中每个点距离。考虑如何算第三部分距离。
第三部分一定是左边某个点通过中间那条边到右边某个点。
可以看出中间那条边对答案的贡献是左边树的大小*右边成树的大小*L。
右边选哪个点跟左边选哪个点没有关系。可以吧
令g[j][p1]表示j这棵树所有点到p1的距离和。
最后对答案的贡献是g[j][p1]*size[Tk]+size[Tj]*g[k][p2]。
考虑如何求g数组。
发现每棵树都由两棵树拼起来，也就是说每个g数组都可以分成两个子过程求。
g[i][p]=g[j][p]+(l+dis[j][p][p1])+g[k][p2]。
但是g的第二维可能有2^60会炸，所以要开map做记忆化搜索，不用算所有可能状态值。
考虑如何求dis数组。
球法类似g，考虑p1和p在不在同一棵树即可。
dis[i][p1][p2]=dis[j][p1][p2]
或dis[i][p1][p2]=dis[j][p1][p2]+dis[k][p3][p4]
对dis记忆化搜索一下即可。
*/
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<map>

using namespace std;

const int mo=;
const int maxn=;

int n,id1[maxn],id2[maxn],l[maxn],res[maxn];

long long num1[maxn],num2[maxn],size[maxn];

struct rec
{
    int p;
    long long p1,p2;
    rec(){}
    rec(int a,long long b,long long c)
    {
        p=a;
        if (b<c) p1=b,p2=c;
        else p1=c,p2=b;
    }
    bool operator<(const rec &a)const
    {
        if (p!=a.p) return p<a.p;
        if (p1!=a.p1) return p1<a.p1;
        return p2<a.p2;
    }
};

map< pair<int,long long > ,int > ma;

map<rec,int> ma2;

int solve(int p,long long p1,long long p2)
{
    if (!p) return ;
    if (p1==p2) return ;
    rec x=rec(p,p1,p2);
    if (ma2.count(x)) return ma2[x];
    if (p1<size[id1[p]])
    {
        if (p2<size[id1[p]]) ma2[x]=solve(id1[p],p1,p2);
        else ma2[x]=((long long)solve(id1[p],num1[p],p1)+solve(id2[p],num2[p],p2-size[id1[p]])+l[p])%mo;
    }
    else
    {
        if (p2<size[id1[p]]) ma2[x]=((long long)solve(id1[p],num1[p],p2)+solve(id2[p],num2[p],p1-size[id1[p]])+l[p])%mo;
        else ma2[x]=solve(id2[p],p1-size[id1[p]],p2-size[id1[p]]);
    }
    return ma2[x];
}

int solve(int p,long long n)
{
    if (p==) return ;
    pair<int,long long> px;
    px=make_pair(p,n);
    if (ma.count(make_pair(p,n))) return ma[px];
    if (n<size[id1[p]]) ma[px]=(((long long)solve(id1[p],num1[p],n)+l[p])*(size[id2[p]]%mo)%mo+solve(id2[p],num2[p])+solve(id1[p],n))%mo;
    else ma[px]=(((long long)solve(id2[p],num2[p],n-size[id1[p]])+l[p])*(size[id1[p]]%mo)%mo+solve(id1[p],num1[p])+solve(id2[p],n-size[id1[p]]))%mo;
    return ma[px];
}

int main()
{
    freopen("cloth.in","r",stdin);
    freopen("cloth.out","w",stdout);

    while (~scanf("%d",&n))
    {
        ma.clear();
        ma2.clear();
        for (int a=;a<=n;a++)
            scanf("%d%d%I64d%I64d%d",&id1[a],&id2[a],&num1[a],&num2[a],&l[a]);
        size[]=;
        for (int a=;a<=n;a++)
            size[a]=size[id1[a]]+size[id2[a]];
        for (int a=;a<=n;a++)
            res[a]=((long long)solve(id1[a],num1[a])*(size[id2[a]]%mo)%mo+(long long)(size[id1[a]]%mo)*(size[id2[a]]%mo)%mo*l[a]%mo+(long long)solve(id2[a],num2[a])*(size[id1[a]]%mo)%mo+res[id1[a]]+res[id2[a]])%mo;
        for (int a=;a<=n;a++)
            printf("%d\n",res[a]);
    }
    return ;
}