BZOJ1742: [Usaco2005 nov]Grazing on the Run 边跑边吃草

数轴上n<=1000个点，从p出发以任意顺序走到所有的点，求到达每个点的时间之和的最小值。

好题！看起来水水的实际易错！

显然的结论是经过一个区间点之后肯定落在左端点或右端点上，谁没事最后还往中间跑呢！那就可以拍个序然后设计dp状态了，一个区间dp，f[i,j,0/1]表示走了区间i~j，最后落在左/右端点。

一个小技巧是把p算成一个点，初始化时之后p这个状态为0，其他都inf。那么问题来了！

方法一：记到状态的时间t[i,j,0/1]，那么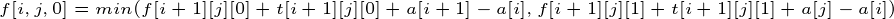，相应更新t，其他同理。

 #include<stdio.h>
 #include<string.h>
 #include<stdlib.h>
 #include<algorithm>
 //#include<iostream>
 using namespace std;
 
 int n,p;
 #define maxn 1011
 int a[maxn],f[maxn][maxn][],t[maxn][maxn][];
 const int inf=0x3f3f3f3f;
 int min(int a,int b) {return a<b?a:b;}
 int main()
 {
     scanf("%d%d",&n,&p);
     for (int i=;i<=n;i++) scanf("%d",&a[i]);
     sort(a+,a++n);
     for (int i=;i<=n;i++) f[i][i][]=f[i][i][]=t[i][i][]=t[i][i][]=inf;
     a[n+]=inf;int pos;
     for (pos=;pos<=n+;pos++) if (a[pos]>p) break;
     if (pos==n+) t[n][n][]=t[n][n][]=f[n][n][]=f[n][n][]=p-a[n];
     else if (pos==) t[][][]=t[][][]=f[][][]=f[][][]=a[]-p;
     else f[pos][pos][]=f[pos][pos][]=a[pos]-p,f[pos-][pos-][]=f[pos-][pos-][]=p-a[pos-],
          t[pos][pos][]=t[pos][pos][]=a[pos]-p,t[pos-][pos-][]=t[pos-][pos-][]=p-a[pos-];
     for (int len=;len<n;len++)
         for (int i=;i<=n-len;i++)
         {
             const int j=i+len;
             if (f[i+][j][]+t[i+][j][]+a[i+]-a[i]<f[i+][j][]+t[i+][j][]+a[j]-a[i])
             {
                 t[i][j][]=t[i+][j][]+a[i+]-a[i];
                 f[i][j][]=f[i+][j][]+t[i][j][];
             }
             else
             {
                 t[i][j][]=t[i+][j][]+a[j]-a[i];
                 f[i][j][]=f[i+][j][]+t[i][j][];
             }
             if (f[i][j-][]+t[i][j-][]+a[j]-a[i]<f[i][j-][]+t[i][j-][]+a[j]-a[j-])
             {
                 t[i][j][]=t[i][j-][]+a[j]-a[i];
                 f[i][j][]=f[i][j-][]+t[i][j][];
             }
             else
             {
                 t[i][j][]=t[i][j-][]+a[j]-a[j-];
                 f[i][j][]=f[i][j-][]+t[i][j][];
             }
             f[i][j][]=min(f[i][j][],inf);
             f[i][j][]=min(f[i][j][],inf);
         }
     printf("%d\n",min(f[][n][],f[][n][]));
     return ;
 }

错误！递推式不成立，没有考虑当前决策对后续状态的影响。错误样例？自己找个标程对拍吧！

方法二：直接把状态对后面的影响算出来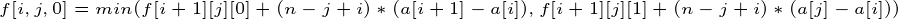，，保证了无后效性。

 #include<stdio.h>
 #include<string.h>
 #include<stdlib.h>
 #include<algorithm>
 //#include<iostream>
 using namespace std;
 
 int n,p;
 #define maxn 1011
 int a[maxn],f[maxn][maxn][];
 const int inf=0x3f3f3f3f;
 int min(int a,int b) {return a<b?a:b;}
 int main()
 {
     scanf("%d%d",&n,&p);
     for (int i=;i<=n;i++) scanf("%d",&a[i]);
     a[++n]=p;
     sort(a+,a++n);
     for (int i=;i<=n;i++)
     {
         if (a[i]!=p) f[i][i][]=f[i][i][]=inf;
         else f[i][i][]=f[i][i][]=;
     }
     for (int len=;len<n;len++)
         for (int i=;i<=n-len;i++)
         {
             const int j=i+len;
             f[i][j][]=min(inf,min(f[i+][j][]+(n-j+i)*(a[i+]-a[i]),f[i+][j][]+(n-j+i)*(a[j]-a[i])));
             f[i][j][]=min(inf,min(f[i][j-][]+(n-j+i)*(a[j]-a[i]),f[i][j-][]+(n-j+i)*(a[j]-a[j-])));
         }
     printf("%d\n",min(f[][n][],f[][n][]));
     return ;
 }

此题在九月份错过一次。

BZOJ1694一样哦！然而又错了，一看原题一激动忘排序了。