寒武纪camp Day3

补题进度：9/10

A(多项式)

题意：

　　在一个长度为n=262144的环上，一个人站在0点上，每一秒钟有$\frac{1}{2}$的概率待在原地不动，有$\frac{1}{4}$的概率向前走一步，有$\frac{1}{4}$概率向后走一步，问t秒后这个人在x点的概率是多少，结果模998244353

分析：

　　我们设：

　　　　留在原地：$1$

　　　　前进一步：$x$

　　　　后退一步：$x^{-1}$

　　那么最后实际上是要求n=262144意义下$(\frac{x^{-1}}{4}+\frac{1}{2}+\frac{x}{4})^t$的第x项的系数

　　因为n是p-1的因数，所以可以选n个单位根快速幂求值，然后NTT插值插出多项式即可。

　　时间复杂度O(nlogn)

B(JAVA/模大质数)

略

C(LIS)

略

D(行列式+容斥)

题意：

　　给出一个长度为n的数组a，其中$a_i<a_{i+1}$

　　有n个机器人，第i个机器人在平面上的$(-a_i,a_i)$位置，每一秒钟可以向上走一步或者向右走一步

　　有n个终点，第i个终点在平面上的$(a_{n+i-i},m-a_{n+i-i})$位置，其中m是给定常数

　　在同一秒中同一个位置不能有两个机器人

　　现在每个机器人都要到它对应的终点去，问有多少合法的不冲突的走路方案，答案模p

　　1<=n<=100,1<=m<=1e18,2<=p<=1e9+7，0<=$a_i$<=1000

分析：

　　 我们发现两个机器人在同一秒在同一个位置这与它们的路径相交是等价的，于是问题就变成了求路径互相不相交的方案数

　　这个就利用16年多校的一个用行列式来容斥的题的套路差不多了，具体就是$a_{i,j}$表示第i个机器人走到第j个终点的方案数，然后求$det a$的值就是最后的结果了

　　这里注意到每个机器人走的步数一定都是m，那么第i个机器人走到第j个终点的方案数就是C(m,a[i]+a[n-j+1])

　　于是我们要想办法快速求出C(m,0),C(m,1),....,C(m,2000)

　　有一个$O(2000^2 * log(m))$的倍增方法来计算它

　　具体就是C(2m,i)=C(m,0)*C(m,i)+C(m,1)*C(m,i-1)+...+C(m,i)*C(m,0)，即要从2m个数中挑i个，我可以将2m个数分成左右两部分，左右两部分各自挑，总和是i就行了

　　然后因为是模非质数，所以求行列式就不能直接求逆了，可以用辗转相减法求行列式

 #include<bits/stdc++.h>
 using namespace std;
 const int maxn=;
 int c[maxn+],x[maxn+];
 int a[maxn+][maxn+];
 int n,mod;
 long long m,ans;
 void cal(long long m)
 {
     if(m==)
     {
         c[]=;
         return;
     }
     if(m&)
     {
         cal(m-);
         for(int i=maxn;i>;--i) c[i]=(c[i]+c[i-])%mod;
     }
     else
     {
         cal(m/);
         for(int i=maxn;i>;--i)
             for(int j=;j<i;++j)
                 c[i]=(c[i]+1LL*c[j]*c[i-j])%mod;
     }
 }
 int main()
 {
     scanf("%d%lld%d",&n,&m,&mod);
     cal(m);
     for(int i=;i<=n;++i) scanf("%d",&x[i]);
     for(int i=;i<=n;++i)
         for(int j=;j<=n;++j)
             a[i][j]=c[x[i]+x[n-j+]];
     ans=;
     cout<<clock()<<endl;
     for(int i=;i<=n;++i)
         for(int j=i+;j<=n;++j)
             while(a[j][i])
             {
                 int d=a[i][i]/a[j][i];
                 for(int k=;k<=n;++k)
                 {
                     a[i][k]=(a[i][k]-1LL*d*a[j][k]%mod+mod)%mod;
                     swap(a[i][k],a[j][k]);
                 }
                 ans=-ans;
             }
     ans=(ans+mod)%mod;
     for(int i=;i<=n;++i) ans=ans*a[i][i]%mod;
     printf("%lld\n",ans);
     return ;
 }

E(线段树)

题意：

　　有一个长度为n的数组a，要支持两个操作：

　　0 l r x ：在[l,r]中的$\frac{(r-l+1)(r-l+2)}{2}$个子区间中等概率随机选一个，给其中的所有数加上x

　　1 l r    ：在[l,r]中的$\frac{(r-l+1)(r-l+2)}{2}$个子区间中等概率随机选一个，问这个子区间的和的期望是多少

　　答案对998244353求模

　　1<=n<=100000,1<=m<=100000

分析：

　　可以推一波式子，发现加操作相当于给一段区间加上一个二次函数$ax^2+bx+c$，询问相当于问一段区间每个位置乘上一个二次函数之后的和

　　我们可以用线段树维护一段区间[l,r]的Σa[i]、Σi*a[i]、Σi^2a[i]就能把每个询问拆成三部分然后累加求和了

　　对于修改我们打lazy就行了

F(AC自动机+容斥+矩乘)

题意：

　　给出n个字符串，问长度为l的字符串有多少个是包含了这n个字符串作为子串的。

　　0<=l<=1e9,1<=n<=8，每个串长度不超过6

分析：

　　如果l比较小，那就建个AC自动机，然后在上面跑状压DP就行了，dp[i][j][s]表示跑了i步在AC自动机的j点，字符串包含情况是S的情况下的方案数

　　但现在问题是l很大，考虑把第一维用矩阵乘法代替

　　那么很容易想到建一个k=48*256的转移矩阵，然后矩阵快速幂

　　这是可以在O(klogk logl)的时间内完成的（用FFT优化O(k^2logl)的算法），但不是很好写而且常数巨大

　　这题n比较小可以考虑把这些字符串容斥，我们每次求出“至少不经过这样几个串的方案数”，就是1<<n次k=48的矩阵乘法，用O(k^3logl)的算法即可

G(FWT)

题意：

　　FWT

分析：

　　FWT真板子题

H(递推数列循环节)

待填坑

I(图论构造)

略

J(polya计数)

题意：

　　你需要给n*m矩阵的每个格子填上0/1

　　矩阵循环平移之后如果相同则视为相同

　　矩阵每一行的异或和、每一列的异或和必须是0

　　你需要求出有多少种本质不同的染色方案

　　n,m<=1e9

分析：

　　明显的二维polya计数，如果没有“同行同列异或和为0”这一限制，那答案明显就是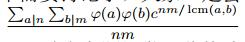

　　其中a和b分别是行/列的循环节长度，即n/a,m/b分别是行、列的平移量，我们来讨论该种置换下不动点的个数

　　原本自由变元的数目是nm/lcm(a,b)，现在有了“同行同列异或和为0”这一限制，我们需要牺牲一些自由变元

　　我们首先来考虑行限制，行限制应该是类似下面这种的：

　　1 xor 2 xor 3 xor 1 xor 2 xor 3 xor 1 xor 2 xor 3 ...... =0

　　4 xor 5 xor 6 xor 4 xor 5 xor 6 xor 4 xor 5 xor 6 .......=0

　　.....

　　那么本质不同的行限制方程明显有n/a个，即行循环的步长，那么这n/a个方程是不是都有效呢？

　　我们还要考虑同一行中所有数字的重复次数，如果是奇数，那么这个方程是有效的，如果是偶数，那么是恒等于0的，是无效的

　　那么循环次数是多少呢？

　　一个数字再矩阵中一共出现l次，在同一列出现了a次，所以一共会在l/a列出现，即同一行每个数字会出现l/a次，我们只需要判断l/a的奇偶性就可以了

　　对于列限制我们同理去考虑

　　然后拿刚开始的自由元去减去有效方程的个数，就是真正自由元的数目

　　注意，如果l/a l/b都是奇数，那么这两组方程会导出一个无效方程（就是把所有的行限制异或起来和把所有列限制异或起来会得到矩阵的整体异或方程），所以自由元需要减去1

　　注意实现精妙一些就行，我们可以先把n,m质因数分解，然后dfs去构造他们的因数，因为这样比较方便在构造过程中求出每个的欧拉函数

 #include<bits/stdc++.h>
 using namespace std;
 #define mp make_pair
 const int mod=1e9+;
 vector<pair<int,int> > A,B,a,b;
 int n,m;
 void prime(vector<pair<int,int> > &a,int x)
 {
     int limit=sqrt(x+0.5);
     for(int i=;i<=limit;++i)
         if(x%i==)
         {
             int s=;
             while(x%i==) x/=i,++s;
             a.push_back(mp(i,s));
         }
     if(x!=) a.push_back(mp(x,));
 }
 void dfs(vector<pair<int,int> > &A,vector<pair<int,int> > a,int k,int factor,int fai)
 {
     if(k==a.size()) A.push_back(mp(factor,fai));
     else
     {
         for(int i=;i<=a[k].second;++i)
         {
             dfs(A,a,k+,factor,fai);
             factor=factor*a[k].first;
             if(i==) fai=fai*(a[k].first-);else fai=fai*a[k].first;
         }
     }
 }
 long long Pow(long long a,long long b)
 {
     long long ans=;
     while(b)
     {
         if(b&) ans=ans*a%mod;
         a=a*a%mod;
         b>>=;
     }
     return ans;
 }
 int main()
 {
     int T;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d%d",&n,&m);
         a.clear(),b.clear(),A.clear(),B.clear();
         prime(a,n);
         prime(b,m);
         dfs(A,a,,,);
         dfs(B,b,,,);
         long long sum=;
         for(int i=;i<A.size();++i)
             for(int j=;j<B.size();++j)
             {
                 long long ans=;
                 ans=ans*A[i].second%mod*B[j].second%mod;
                 long long lcm=1LL*A[i].first/__gcd(A[i].first,B[j].first)*B[j].first;
                 long long num=1LL*n*m/lcm;
                 if(lcm/A[i].first%==&&lcm/B[j].first%==) num-=n/A[i].first+m/B[j].first-;
                 else
                     if(lcm/A[i].first%==) num-=n/A[i].first;
                     else
                         if(lcm/B[j].first%==) num-=m/B[j].first;
                 ans=ans*Pow(2LL,num)%mod;
                 sum=(sum+ans)%mod;
             }
         printf("%lld\n",sum*Pow(1LL*n,1LL*mod-)%mod*Pow(1LL*m,1LL*mod-)%mod);
     }
     return ;
 }