C++ 函数部分（2）

C++函数的递归调用

函数可以直接或间接地调用自身，称为递归调用。所谓直接调用自身，就是指在一个函数的函数体中出现了对自身的调用表达式，例如：

void fun1(void)

    //do something

    fun1(); //调用fun1自身

    //do something

.csharpcode, .csharpcode pre
{
font-size: small;
color: black;
font-family: consolas, "Courier New", courier, monospace;
background-color: #ffffff;
/*white-space: pre;*/
}
.csharpcode pre { margin: 0em; }
.csharpcode .rem { color: #008000; }
.csharpcode .kwrd { color: #0000ff; }
.csharpcode .str { color: #006080; }
.csharpcode .op { color: #0000c0; }
.csharpcode .preproc { color: #cc6633; }
.csharpcode .asp { background-color: #ffff00; }
.csharpcode .html { color: #800000; }
.csharpcode .attr { color: #ff0000; }
.csharpcode .alt
{
background-color: #f4f4f4;
width: 100%;
margin: 0em;
}
.csharpcode .lnum { color: #606060; }

函数间接调用自身，就是通过调用其它函数的同时在其它函数中有调用了自己，例如：

void fun1(void)

    //do something

    fun2(); //调用fun1自身

    //do something

void fun2(void)

    //do something

    fun1();

    //do something

这里fun1调用了fun2,而fun2又调用了fun1, 于是就构成了递归。

递归算法的实质是将原有的问题分解为新的问题，而解决新问题时又用到了原有问题的解法。按照这一原则分解下去，每次出现的新问题都是原有问题的简化的子集，而最终分解出来的问题，是一个已知解的问题。

递归的过程有两个阶段：

第一个阶段：递推。讲原问题不断分解为新的子问题，逐渐从未知向已知推进，最终达到已知的条件，即递归结束的条件，这时递推阶段结束。例如，求5！，可以这样分解：

5！= 5*4！->4！=4*3！->3! =3*2! –> 2!=2*1!->1! = 1*0!->0! =1

未知--------------------------------------------------------------------->已知

第二阶段：回归。从已知条件出发，按照递推的逆过程，逐一求值回归，最后达到递推的开始处，结束回归阶段，完成递归调用。例如，求5！的回归阶段如下：

5！= 5*4！<- 4！=4*3！<- 3! =3*2! <– 2!=2*1! <- 1! = 1*0! <- 0! =1

未知<--------------------------------------------------------------------- 已知

1.求n!的值

分析：计算n!的公式如下：

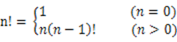
这是一个递归形式的公式，在描述"阶乘"算法时又用到了"阶乘"。递归的结束条件是 n = 0.

#include <iostream>

using namespace std;

long fac(int n)

    long f;

    if(n<0) cout<<"n<0,data error!"<<endl;

    else if(n == 0) f = 1;

    else f = fac(n-1)*n;

    return (f);

void main()

    long fac(int n);  //函数声明

    int n;

    long y;

    cout<<"Enter a positive integer: ";

    cin>>n;

    y = fac(n);

    cout<<n<<"! = "<<y<<endl;

    fflush(stdin);

    getchar();

2.用递归法计算从n个人中选择k个人组成一个委员会的不同组合数。

分析：由n个人里选k个人的组合数 = 由（n-1)个人里选k个人的组合数 + 由（n-1)个人里选(k-1)个人的组合数。递推的结束条件是n == k || k == 0 ，这时的组合数为1。

#include <iostream>

using namespace std;

void main()

    int n, k;

    int comm(int n , int k);

    cout<<"Enter n and k :";

    cin>>n>>k;

    cout<<comm(n,k)<<endl;

    fflush(stdin);

    getchar();

int comm(int n, int k)

    if(k>n) return 0;

    else if(n == k || k == 0) return 1;

    else

        return comm(n-1,k)+comm(n-1,k-1);

结果：

input 18 5 output : 8568

3. 汉诺塔问题

有三根针A、B、C。A针上有n个盘子，盘子大小不等，大的在下，小的在上，如下图所示。要求把这n个盘子从A针移动到C针，在移动过程中可以借助B针，每次只充许移动一个盘子，且在移动过程中在三根针上都保持大盘在下，小盘在上。

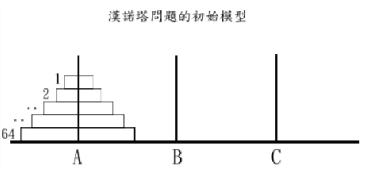
分析:

将n个盘子从A针移动到C针可以分解为下面3个步骤：

1.将A上n-1个盘子移动到B针上（借助C针）；

2.把A针上剩下的一个盘子移动到C针上；

3.将n-1个盘子从B针移动到C针上（借助A针）

事实上，上面3个步骤包含两种操作：

1.将多个盘子从一个针移动到另一个针上，这是一个递归的过程。

2.将1个盘子从一个针上移动到另一个针上。

那么就可以用两个函数分别实现上面的两种操作，用hanoi函数实现第一种操作，用move函数实现第二种操作。

#include <iostream>

#include <iomanip>

using namespace std;

void move(char getone, char putone)

    static int i = 1;

    cout<<"Step."<<setw(2)<<i<<" : "<<getone<<"-->"<<putone<<endl;

    i++;

void hanoi(int n, char one, char two,char three)

    void move(char getone , char putone);

    if(n == 1) move(one , three);

    else

        hanoi(n-1,one,three,two);

        move(one,three);

        hanoi(n-1,two,one, three);

void main()

    void hanoi(int n , char one , char two, char three);

    int m;

    cout<<"Enter the number of diskes : " ;

    cin>>m;

    cout<<"the steps to moving "<<m<<" diskes:"<<endl;

    hanoi(m,'A','B','C');

    fflush(stdin);

    getchar();

运行结果：

Enter the number of diskes : 3

the steps to moving 3 diskes:

Step. 1 : A-->C

Step. 2 : A-->B

Step. 3 : C-->B

Step. 4 : A-->C

Step. 5 : B-->A

Step. 6 : B-->C

Step. 7 : A-->C

函数的参数传递

在函数为被调用时，函数的形参并不占有实际的内存空间，也没有实际的值。只有在函数被调用时才为形参分配存储单元，并将实参与形参结合。结合过程叫做参数传递，有值传递和引用传递两种方式。

1.值传递

值传递是指当发生函数调用时，给形参分配内存空间，并用实参来初始化形参（直接将实参的值传递给形参）。这一过程是参数值的单向传递过程，一旦形参获得了值便与实参脱离关系，此后无论形参发生了怎样的改变，都不会影响到实参。

#include <iostream>

using namespace std;

void swap(int a ,int b);

void main()

    int x(5),y(10);

    cout<<"x = "<<x<<" y = "<<y<<endl;

    swap(x,y);

    cout<<"x = "<<x<<" y = "<<y<<endl;

    fflush(stdin);

    getchar();

void swap(int a, int b)

    int t;

    t = a;

    a = b;

    b = t;

上例中，swap之前x,y分别初始化为5和10，调用swap时，实参x,y把值传递给形参a,b 由于这里是值传递，是单向的，所以实参x,y把值5，10传递给a,b之后就跟a,b没有关系了，在swap里面a，b借助临时变量t交换了值，但是这是a,b之间交换了值不影响x,y的值。

2.引用传递

引用是一种特殊类型的变量，可以被认为是另一个变量的别名。通过引用名与通过被引用的变量名访问变量的效果是一样的，例如：

int i,j;

int &r = i; // 建立一个int型的引用r，并将其初始化为变量i的一个别名

j = 10;

r = j; //相当于i = j;

使用引用时需要注意两个问题：

1.声明一个引用时，必须同时对它进行初始化，使它指向一个已存在的对象。

2.一旦一个引用被初始化后，就不能改为指向其它对象。也就是说，一个引用，从它诞生之时起，就必须确定是哪个变量的别名，而且始终只能作为这个变量的别名，不能另作它用。

&放在变量前面就是引用符号

#include <iostream>

using namespace std;

void swap(int& a, int& b);

void main()

    int x(5), y(10);

    cout<<"x = "<<x<<"   y = "<<y<<endl;

    swap(x,y);

    cout<<"x = "<<x<<"   y = "<<y<<endl;

    fflush(stdin);

    getchar();

void swap(int&a , int& b)

    int t;

    t = a;

    a = b;

    b = t;

引用传递与值传递的区别只是函数的形参写法不同，主调函数中的调用表达式完全一样。

内联函数

函数调用时，需要保存现场和返回地址，然后转到子函数的代码起始地址去执行。子函数执行完后，又要取出先前保存的返回地址和现场状态，再继续执行。这一切都需要时间和空间方面的开销，所以频繁调用函数会降低程序的执行效率。对于一些功能简单、规模较小又使用频繁的函数，可以设计为内联函数。内联函数不是在调用时发生控制转移，而是在编译时将函数体嵌入在每个调用处。这样就节省了参数传递、控制转移等开销。

内联函数在定义时使用关键字inline，语法形式如下：

inline 类型说明符被调函数名（含类型说明的形参表）｛函数体语句;｝

使用内联函数时应注意：

1.内联函数体内一般不能有循环语句和switch语句；

2.内联函数的定义必须出现在第一次被调用之前；

3.对内联函数不能进行异常接口声明

通常内联函数应该是比较简单的函数，结构简单、语句少。如果将一个复杂的函数定义为内联函数，反而会造成代码膨胀，增大开销。这种情况下，多数编译器都会自动将其转换为普通函数来处理。

因此，inline关键字只是表示一个要求，编译器并不承诺将inline修饰的函数作为内联。而没有用inline修饰的函数也可能编译为内联函数。

C++中充许给函数设置默认的形参值

函数在定义时可以预先声明默认的形参值。调用时如果给出实参，则用实参初始化形参；如果没有给出实参，则采用预先声明的默认形参值。例如：

 int add(int x = 5, int y = 6) // 声明默认形参值

        return x + y;

void main(void)

    add(10,20); //用实参来初始化形参，实现10+20

    add(10); //形参x采用实参值10，y采用默认值6， 实现10+6

    add();  //x和y都采用默认值，分别为5和6，实现5+6

默认形参值必须按从右向左的顺序声明。在有默认值的形参值右面，不能出现无默认值的形参。因为在调用时，实参初始化形参是按从左向右的顺序。例如：

int add(int x , int y = 5, int z = 6); //正确

int add(int x = 1, int y = 5, int z); //错误

int add(int x = 1 , int y, int z = 6);// 错误

默认形参值应该在函数原型中给出，例如：

int add(int x = 5, int y = 6); //默认形参值在函数原型中给出

void main(void)

{

add();

}

int add(int x ,int y)

{

retrun (x + y);

}

注意：在相同的作用域内，默认形参值的说明应保持唯一，但如果在不同的作用域内，充许说明不同的默认形参，例如：

int add(int x = 1, int y = 2);

void main(void)

    int add(int x = 3, int y = 5);

    add(); //使用局部默认形参值(实现3+5)

void fun(void)

    //do something

    add(); //使用全局默认形参值(实现1+2)

C++的函数重载，就是通过调用相同的函数名来响应不同的操作。在两个以上的函数中，具有相同的函数名，但是形参的个数或类型不同，编译器根据实参和形参的类型及个数的最佳匹配，自动确定调用哪个函数，这就是函数的重载。

1.判断一个数是否为质数（质数又称为素数）

质数又称之为素数。指在一个大于1的自然数中，除了1和此整数自身外，没法被其它自然数整除的数。即只有两个正因数（1和自己）的自然数即为素数。比1大但不是素数的数称为合数。1和0既非素数也非合数。合数是由若干个质数相乘而得到的。

取模运算：a % p（或a mod p），表示a除以p的余数。

注意：n % p 得到结果的正负由被除数n决定,与p无关。例如：7%4 = 3， -7%4 = -3， 7%-4 = 3， -7%-4 = -3。

#include <iostream>

#include <math.h>

using namespace std;

int prime(int n);

int main()

    int n;

    cout<<"Enter an integer:";

    cin>>n;

    if(prime(n))

        cout<<n<<"是素数"<<endl;

    else

        cout<<n<<"不是素数"<<endl;

    fflush(stdin);

    getchar();

int prime(int n)

    int j,flag;

    flag = 1;

    for(j = 2; j<=sqrt(double(n));j++)

        if(n % j == 0)

            flag = 0;

            break;

    if(flag)

        return 1;

    else return 0;

最大公约数，也称为最大公因数，最大公因子，指两个或多个整数共有约数中最大的一个。a,b的最大公约数记为（a,b),同样的，a,b,c的最大公约数记为（a,b,c),多个整数的最大公约数也有同样的记号。记号（a)表示a的约束中最大的那个数。与最大公约数相对应的概念是最小公倍数，a,b的最小公倍数记为[a,b]。

如果数a能被数b整除，a就叫做b的倍数，b就叫做a的约数。约数和倍数都表示一个数与另一个数的关系，不能单独存在。

几个自然数，公有的约数，叫做这几个数的公约数；其中最大的一个，叫做这几个数的最大公约数。例如：12，16的公约数有1，2，4，其中最大的一个是4，4是12与16的最大公约数，一般记为（12，16） = 4.

几个自然数公有的倍数，叫做这几个数的公倍数，其中最小的一个，叫做这几个数的最小公倍数。例如：4的倍数有4，8，12，……，6的倍数有6，12，……，4和6的公倍数有12，24，……，其中最小的是12，所以[4,6] = 12.两数互质最小公倍数为两数乘积。

互质又叫互素。若N个整数的最大公因数是1，则称这N个整数互质。例如8，10的最大公因数是2，不是1，因此不是整数互质。7，10，13的最大公因数是1，因此这是整数互质。下面分析两种求最大公约数的方法：

（1）求差判定法．

如果两个数相差不大，可以用大数减去小数，所得的差与小数的最大公约数就是原来两个数的最大公约数．例如：求78和60的最大公约数．78－60＝18，18和60的最大公约数是6，所以78和60的最大公约数是6．

如果两个数相差较大，可以用大数减去小数的若干倍，一直减到差比小数小为止，差和小数的最大公约数就是原来两数的最大公约数．例如：求92和16的最大公约数．92－16＝76，76－16＝60，60－16＝44，44－16＝28，28－16＝12，12和16的最大公约数是4，所以92和16的最大公约数就是4．

（2）辗转相除法．

当两个数都较大时，采用辗转相除法比较方便．其方法是：

以小数除大数，如果能整除，那么小数就是所求的最大公约数．否则就用余数来除刚才的除数；再用这新除法的余数去除刚才的余数．依此类推，直到一个除法能够整除，这时作为除数的数就是所求的最大公约数．

例如：求4453和5767的最大公约数时，可作如下除法．

5767÷4453＝1余1314

4453÷1314＝3余511

1314÷511＝2余292

511÷292＝1余219

292÷219＝1余73

219÷73＝3

于是得知，5767和4453的最大公约数是73．

辗转相除法适用比较广，比短除法要好得多，它能保证求出任意两个数的最大公约数．

而最小公倍数可以借助最大公约数来求，分两步：

1.利用辗除法或其它方法求得最大公约数

2.最小公倍数等于两数之积除以最大公约数

举例：12和8的最大公约数为4，12*8/4 = 24 那么12和8的最小公倍数为24.

C++递归版：

#include<iostream>

using namespace std;

int func(int a, int b)

    int min, max;

    max = a>b?a:b;

    min = a<b?a:b;

    if(max%min ==0)

        return min;

    else

        return func(min,max%min);

int main()

    int a, b;

    cout<<"输入两个整数，用空格分隔，按回车结束：";

    cin>>a>>b;

    cout<<"这两个整数的最大公约数是："<<func(a,b)<<endl;

    cout<<"这两个整数的最小公倍数是："<<((a*b)/func(a,b))<<endl;

    fflush(stdin);

    getchar();

非递归版:

#include<iostream>

using namespace std;

int func(int a, int b)

    int min, max,r;

    max = a>b?a:b;

    min = a<b?a:b;

    if(max%min ==0)

        return min;

     while(max%min != 0)

        r=max%min;

        max = min;

        min =r;

     return min;

int main()

    int a, b;

    cout<<"输入两个整数，用空格分隔，按回车结束：";

    cin>>a>>b;

    cout<<"这两个整数的最大公约数是："<<func(a,b)<<endl;

    cout<<"这两个整数的最小公倍数是："<<((a*b)/func(a,b))<<endl;

    fflush(stdin);

    getchar();

运行结果：

输入两个整数，用空格分隔，按回车结束：12 8

这两个整数的最大公约数是：4

这两个整数的最小公倍数是：24

3.编写递归函数GetPower(int x, int y ) 计算x的y次幂，在主程序中实现输入输出。

int func(int x , int y)

{   static int sum = 1;

    if(y ==1) sum *=x;

    else sum *=func(x,y-1);

    return sum;

因为sum = sum*sum*func(5,1);这里func(5,1)返回的sum会改变前面的sum值，此外这里的运算是自右向左运算的，也就是说返回的sum = 5 ,然后最右边两个sum 运算之后sum值25，然后再于剩下的sum运算，此时是25*25 所以输入5，3之后输出的结果是625.

C++版：

#include <iostream>

using namespace std;

int GetPower(int x, int y)

    if(x == 0) return 0;

    if(y == 0) return 1;

    if(y == 1) return x;

    if(x>1&&y>1) return (GetPower(x,y-1)*x);

int main()

    int a, b;

    cout<<"Input a and b:";

        cin>>a>>b;

    cout<<"The result is: "<<GetPower(a,b)<<endl;

    fflush(stdin);

    getchar();

C++ 函数部分（2）的更多相关文章

Python 小而美的函数
python提供了一些有趣且实用的函数,如any all zip,这些函数能够大幅简化我们得代码,可以更优雅的处理可迭代的对象,同时使用的时候也得注意一些情况 any any(iterable) ...
探究javascript对象和数组的异同，及函数变量缓存技巧
javascript中最经典也最受非议的一句话就是:javascript中一切皆是对象.这篇重点要提到的,就是任何jser都不陌生的Object和Array. 有段时间曾经很诧异,到底两种数据类型用来 ...
JavaScript权威指南 - 函数
函数本身就是一段JavaScript代码,定义一次但可能被调用任意次.如果函数挂载在一个对象上,作为对象的一个属性,通常这种函数被称作对象的方法.用于初始化一个新创建的对象的函数被称作构造函数. 相对 ...
C++对C的函数拓展
一,内联函数 1.内联函数的概念 C++中的const常量可以用来代替宏常数的定义,例如:用const int a = 10来替换# define a 10.那么C++中是否有什么解决方案来替代宏代码 ...
菜鸟Python学习笔记第一天：关于一些函数库的使用
2017年1月3日星期二大一学习一门新的计算机语言真的很难,有时候连函数拼写出错查错都能查半天,没办法,谁让我英语太渣. 关于计算机语言的学习我想还是从C语言学习开始为好,Python有很多语言的 ...
javascript中的this与函数讲解
前言 javascript中没有块级作用域(es6以前),javascript中作用域分为函数作用域和全局作用域.并且,大家可以认为全局作用域其实就是Window函数的函数作用域,我们编写的js代码, ...
复杂的 Hash 函数组合有意义吗？
很久以前看到一篇文章,讲某个大网站储存用户口令时,会经过十分复杂的处理.怎么个复杂记不得了,大概就是先 Hash,结果加上一些特殊字符再 Hash,结果再加上些字符.再倒序.再怎么怎么的.再 Hash ...
JS核心系列：浅谈函数的作用域
一.作用域(scope) 所谓作用域就是:变量在声明它们的函数体以及这个函数体嵌套的任意函数体内都是有定义的. function scope(){ var foo = "global&quo ...
C++中的时间函数
C++获取时间函数众多,何时该用什么函数,拿到的是什么时间?该怎么用?很多人都会混淆. 本文是本人经历了几款游戏客户端和服务器开发后,对游戏中时间获取的一点总结. 最早学习游戏客户端时,为了获取最精确 ...
Python高手之路【四】python函数装饰器
def outer(func): def inner(): print('hello') print('hello') print('hello') r = func() print('end') p ...

随机推荐

string和数值之间的转换
string和数值之间的转换 to_string(val) 一组重载函数,返回数值val的string表示val可以是任何算数类型. stoi(s,p,b),stol(s,p,b),stoul(s,p ...
JustinMind
看到公司老板新请来的兼职产品经理,在讲项目功能设计图是,用的是justinmind这个工具,觉得很好奇,默默记下,或许以后能用到.下面是搜的简单的介绍,只是为了记住这个工具名字,现并没有想要深入探究这 ...
0元免费领《JAVA日志》教程，天啦噜！
天啦,老码疯了!辛辛苦苦,费心费力准备的<java日志实战及解析>教程真的不要钱了吗? 作为添物网的小编,每天看着老码为了给大家录制课程,加班加点的做课件,为了保证课程的质量,老码一遍又一 ...
POJ 3177 边双连通求连通量度的问题
这道题的总体思路就是找到连通量让它能够看作一个集合,然后找这个集合的度,度数为1的连通量为k,那么需要添加(k+1)/2条边才可以保证边双连通这里因为一个连通量中low[]大小是相同的,所以我们用a ...
hdu1856 选出更多的孩子
题目大意: 老师选取2个学生对应的号码,这两人视作朋友,同时朋友的朋友也可以看成自己的朋友. 最后老师选出一个人数最多的朋友圈. 这里学生的人数不大于10^7,所以操作时需要极为注意,操作步数能省则省 ...
Xcode warning：Auto property synthesis will not synthesize property
iOS 警告提示如下: 添加 @dynamic告诉编译器这个属性是动态的,动态的意思是等你编译的时候就知道了它只在本类合成; 如下:
2015轻院校赛 D 社交网络（排列组合）
http://acm.zznu.edu.cn/problem.php?id=1964 题目描述输入输出样例输入 2 2 1 0 1 1 0 3 1 0 1 1 1 0 1 1 1 0 样例输出 ...
洛谷——P1608 路径统计
P1608 路径统计题目描述 “RP餐厅”的员工素质就是不一般,在齐刷刷的算出同一个电话号码之后,就准备让HZH,TZY去送快餐了,他们将自己居住的城市画了一张地图,已知在他们的地图上,有N个地方, ...
strcpy c标准库函数
C语言标准库函数strcpy,把从src地址开始且含有NULL结束符的字符串复制到以dest开始的地址空间. 已知strcpy函数的原型是: char *strcpy(char *dst, const ...
mybatis结合generator进行分页插件PluginAdapter开发
使用org.mybatis.generator生成UserExample时,无法进行分页,使用下面这个类运行generator便可以生成分页相关的属性了 package org.mybatis.gen ...

C++ 函数部分（2）

C++ 函数部分（2）的更多相关文章

随机推荐

热门专题